[DL] 경사 하강법(Gradient Descent)

💡경사하강법

• 인공신경망은 손실 함수를 통해 자신의 파라미터를 검증한다.
• 특정 파라미터를 통해 나온 손실함수 값이 가장 낮은 곳이 최적의 파라미터이다.
• 경사하강법은 비용 함수를 최소화하는 매개변수를 찾기 위해 사용되는 알고리즘이다.
• 한마디로, 주어진 함수에서 극소점을 찾기 위해 기울기(gradient)가 최소가 되는 지점을 찾아가는 방법이다.

✅ gradient descent 비유

gradient descent는 등산을 할 때 정상에서 하산 할때에 많이 비유를 하곤 한다. 특히 우리가 앞이 보이지 않는 안개가 낀 산을 하산을 할때 모든 방향으로 더듬어 보며 비탈길의 경사가 가파른 방향으로 내려갈 것이다.

여기서 산 비탈길의 기울기가 그래프의 기울기로 보면 된다. 이 기울기가 감소하는 즉, gradient 가 descent 하는 방향으로 최적의 값을 찾는 방향으로 학습이 진행된다.
각 지점에서 gradient를 구하기 위해서는 각 점의 순간 변화량을 뜻하는 미분값을 알아야 한다.

📌gradient descent 수식 유도

• 2차 함수 그래프에서 최초 랜덤 위치에서 시작한다고 가정했을 때, 다음 지점은 어디로 가야 하는지에 대한 수식을 유도한다
  
• 현재 지점에서 기울기를 먼저 구한 뒤
• 기울기가 양수인지 음수인지를 판단하고,
• 둘째로 얼마큼 이동할 것 인가(step size)를 정한 뒤 이동
• 위 그림에서 해당 지점의 기울기가 음수일 때는 양의 방향으로 , 양수일 경우는 음의 방향으로 이동하면 함수의 극소점을 찾을 수 있다.
• 얼마만큼 이동할 것인가에 대한 부분인 step size는 α로 많이 표현을 한다.

[gradient descent 수식]

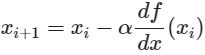
• xᵢ번째 에서의 기울기에 α 인 step size를 곱하고 기울기의 부호의 반대로 움직임으로써 마이너스 기호를 사용하여 xᵢ 번째에서 xᵢ₊₁번째로 이동을 하는 것

📌 경사하강법 순서

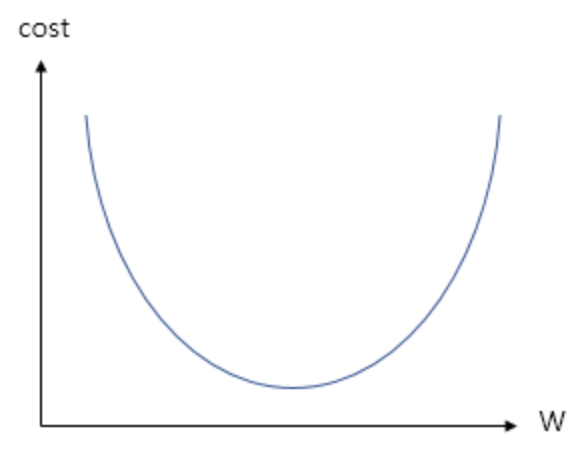
1. 임의의 매개변수를 정해 비용함수의 시작지점(x축)으로 지정.
2. 해당 매개변수로 모델의 오차를 구한 후, 비용함수의 시작지점(y축)으로 지정.
3. 시작 지점에서 다음 지점으로 갈 방향을 정하기 위해, 시작 지점의 기울기를 계산.
4. 기울기(Gradient)와 보폭(Learning rate)을 사용해 다음 지점으로 이동.
5. 위 과정을 최소값에 도달할 때까지 반복.

💡경사 하강법의 문제점

1. 적절한 학습률 (Learning Rate)

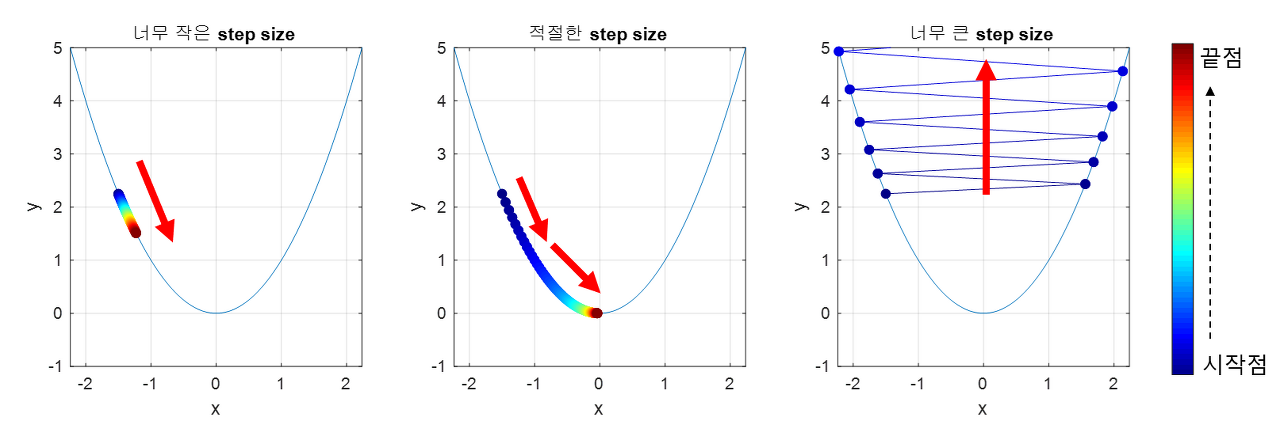
• 학습률과 기울기 정보를 혼합해 나아갈 방향과 거리를 결정한다.
• 학습률이 높으면 한번에 이동하는 거리가 커지므로 최적값에 빨리 수렴할 수 있다.
• 그러나 너무 크게 설정하면 최적값에 수렴하지 못하고, 다른 곳으로 발산하는 현상이 나타날 수 있다.
• 반대로, 학습률이 낮으면 최적값에 수렴하는 시간이 오래 걸릴 수 있다.
• 적절한 learning rate값을 찾는 것이 중요하다.

2. local minimum

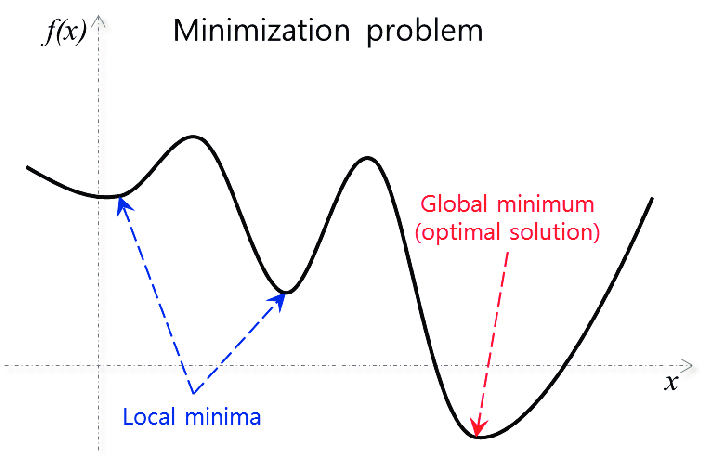
• Global minimum을 목표로 해야하지만 local minimum에 빠지는 경우 탈출하지 못하고 그 점으로 수렴해버릴 수 있다.
• local minima에서 탈출하기 위한 방법으로 momantum이나 stocastic gradient descent와 같은 여러 방법이 존재한다

출처
https://hi-guten-tag.tistory.com/205
https://dotiromoook.tistory.com/25