선형 귀환 쉬프트 레지스너 (Linear-FSR)
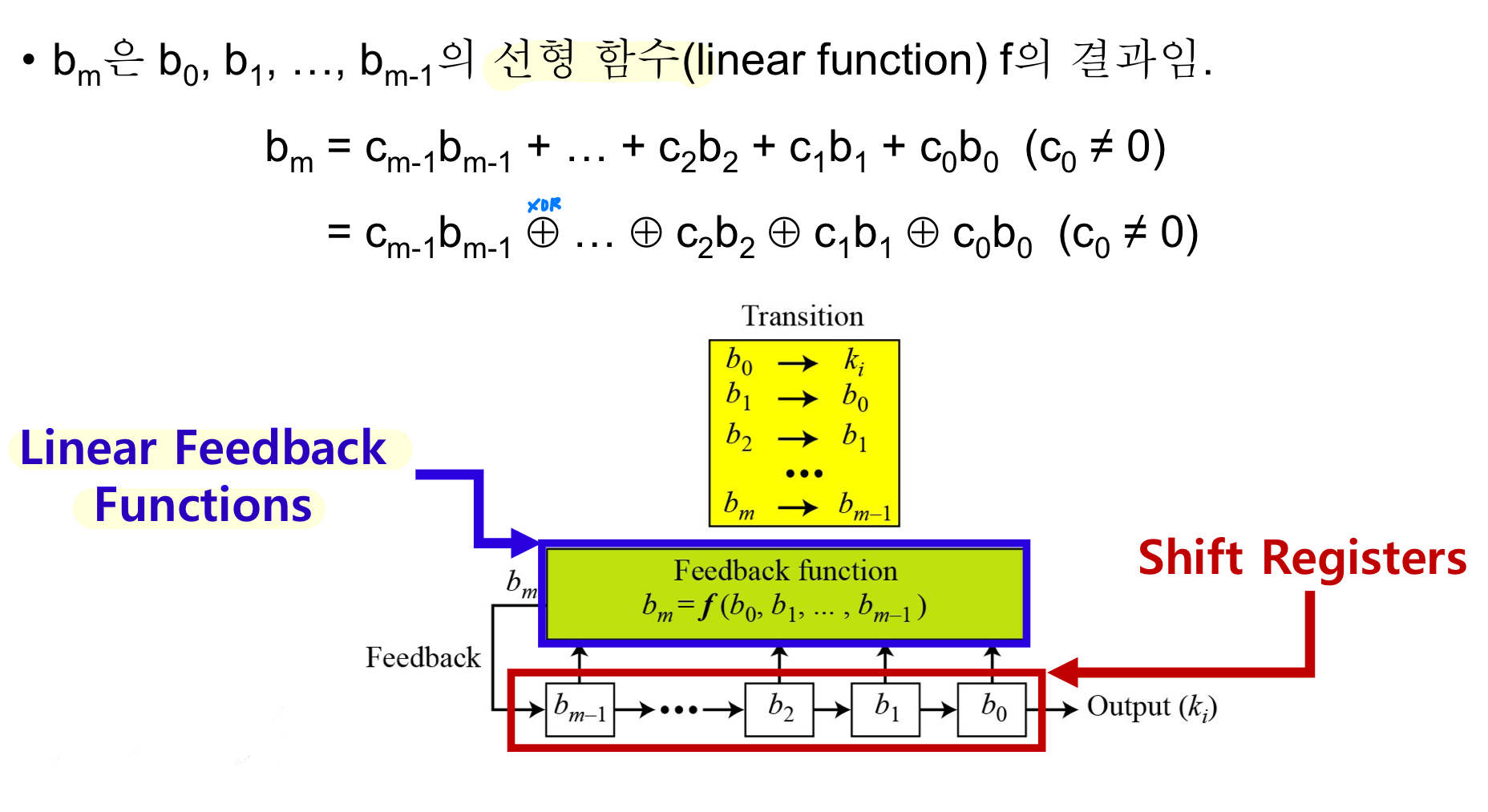
예제1) b5 = b4 ⊕ b2 ⊕ b0을 만족하고 5개의 셀을 갖는 선형 귀환 쉬프트 레지스터를 설계하라.
- ci = 0이면 bi는 bm의 계산에 영향을 주지 않음 -> bi가 귀환 함수에 연결되지 않음을 의미함
- ci = 1이면 bi는 bm의 계산에 영향을 줌
- 이 예제에서 귀환 함수에는 단지 세 개의 셀만이 연결됨을 의미함
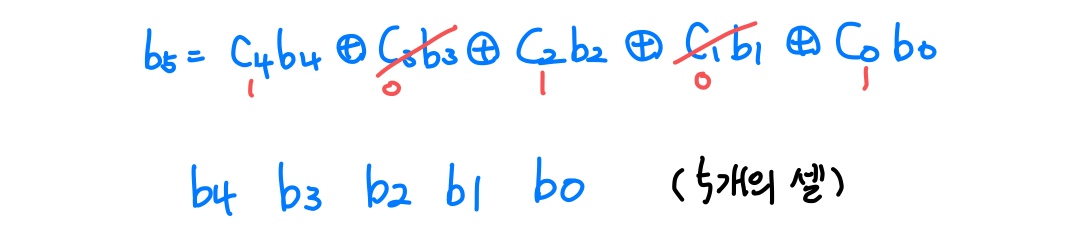
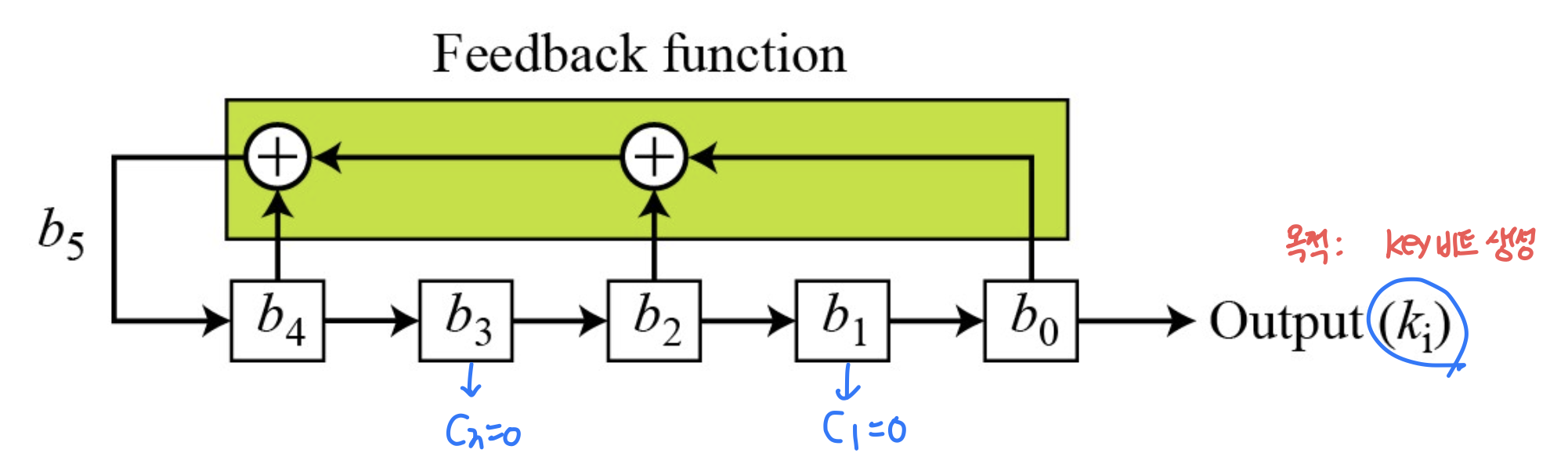
예제2) b4 = b1 ⊕ b0을 만족하고 4개의 셀을 갖는 선형 귀환 쉬프트 레지스터를 설계하라. 또한 seed가 (0001)2일 때, 20번의 변환 후 출력되는 값을 보여라
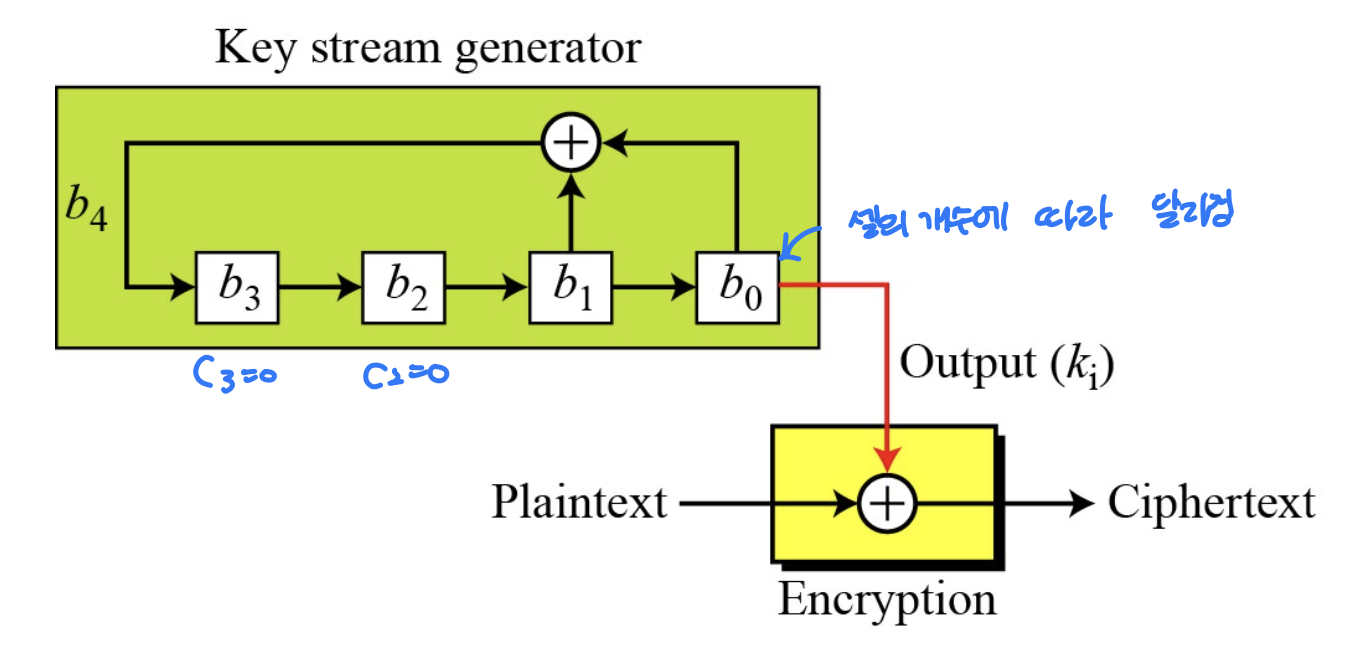
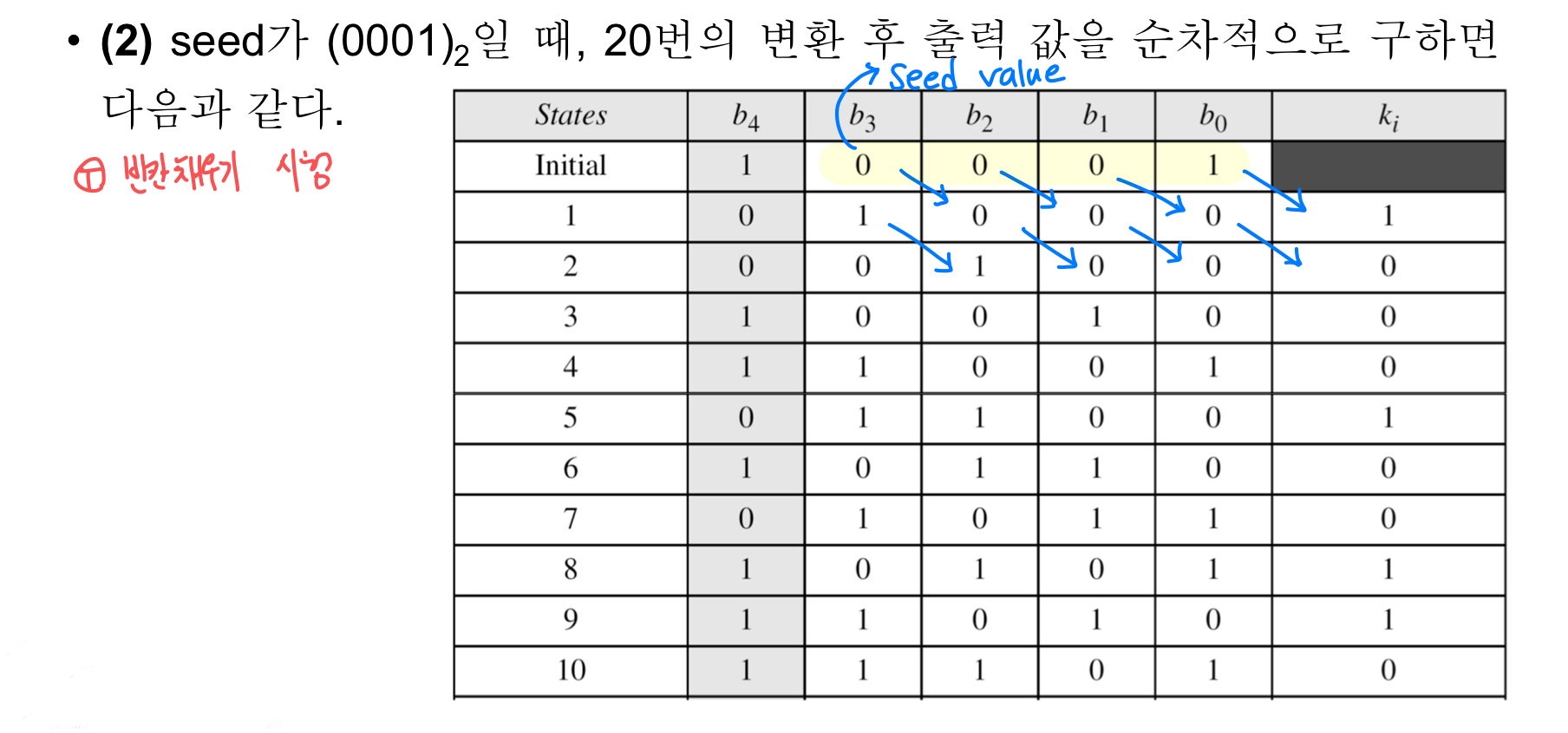
- 예제2에서 설계한 LFSR의 출력 키 스트림이 순환하는가?
- 예제 2에서 구한 표의 ki를 나열하면 키 스트림이 10001001101011110001... 임을 알 수 있음
- 이때, 키 스트림을 더 생성하면 출력되는 키 스트림이 일정한 주기를 가짐을 확인할 수 있음 -> 100010011010111 15비트가 반복됨
- 결과적으로 LFSR에 의해 생성된 키 스트림은 수열이 N비트 이후에 반복되는 의사 난수열임
키 비트열이 일정 주기에서 반복됨
- 공식이 존재하기 때문
- XOR 결과가 일정 주기 이후에 입력으로 들어가기 떄문
선형 귀환 쉬프트 레지스터에 대한 공격
- 공격자가 LFSR의 구조를 이미 알고 있는 경우
- 공격자는 가로챈 n비트 암호문의 분석을 통해 미래의 암호문을 모두 예측할 수 있음
- 공격자가 LFSR의 구조를 모르는 경우
- 공격자는 암호를 깨기 위해 2^n 비트의 알려진 평문 공격을 이용할 수 있음
비선형 귀환 쉬프트 레지스터(Non-Linear FSR)
- LFSR은 선형성 때문에 공격에 취약함
- 따라서 각 쉬프트 함수를 비선형 함수를 사용해 설계함으로써, 보다 안전한 암호 체계를 구축할 수 있음
간단한 비선형 함수 사용의 예
b4 = (b3 AND b2) OR (b1 AND ~b0)
- and가 비트별 논리곱 연산이고, or를 비트별 논리합 연산이며, ~가 보수 연산일 때, 4비트 NLFSR에서 그 관계는 다음과 같이 정의함
- 최대 주기를 갖는 NLFSR을 설계하기 위한 수학적 기초지식이 알려져 있지 않기 때문에 NLFSR이 널리 사용되지는 않음
- 비동기식 스트림 암호에서 키 스트림의 각 비트는 이전의 평문이나 암호문에 종속되어 결정됨
- 비동기식 스트림 암호에서는 서로 다른 암호 운영 모드를 운용함
- OFB(Output Feedback Mode)
- CTR(Counter Mode)
- 상기의 두 모드를 구성하는 방법은 실제로는 스트림 암호를 생성함

