Assembly-line scheduling
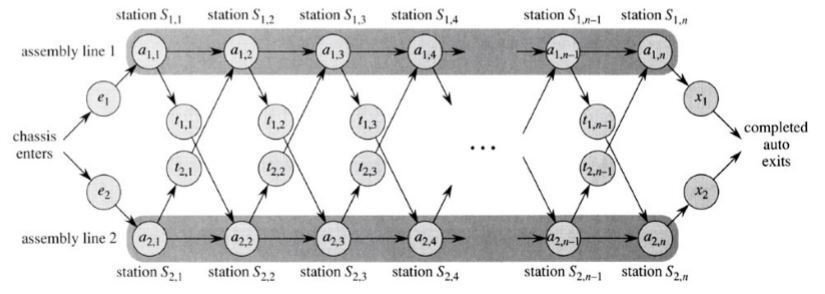
Brute-force approach
- n개의 공정이 존재할 때, 2개의 라인이 존재하므로 총 2^n개의 경우의 수
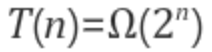
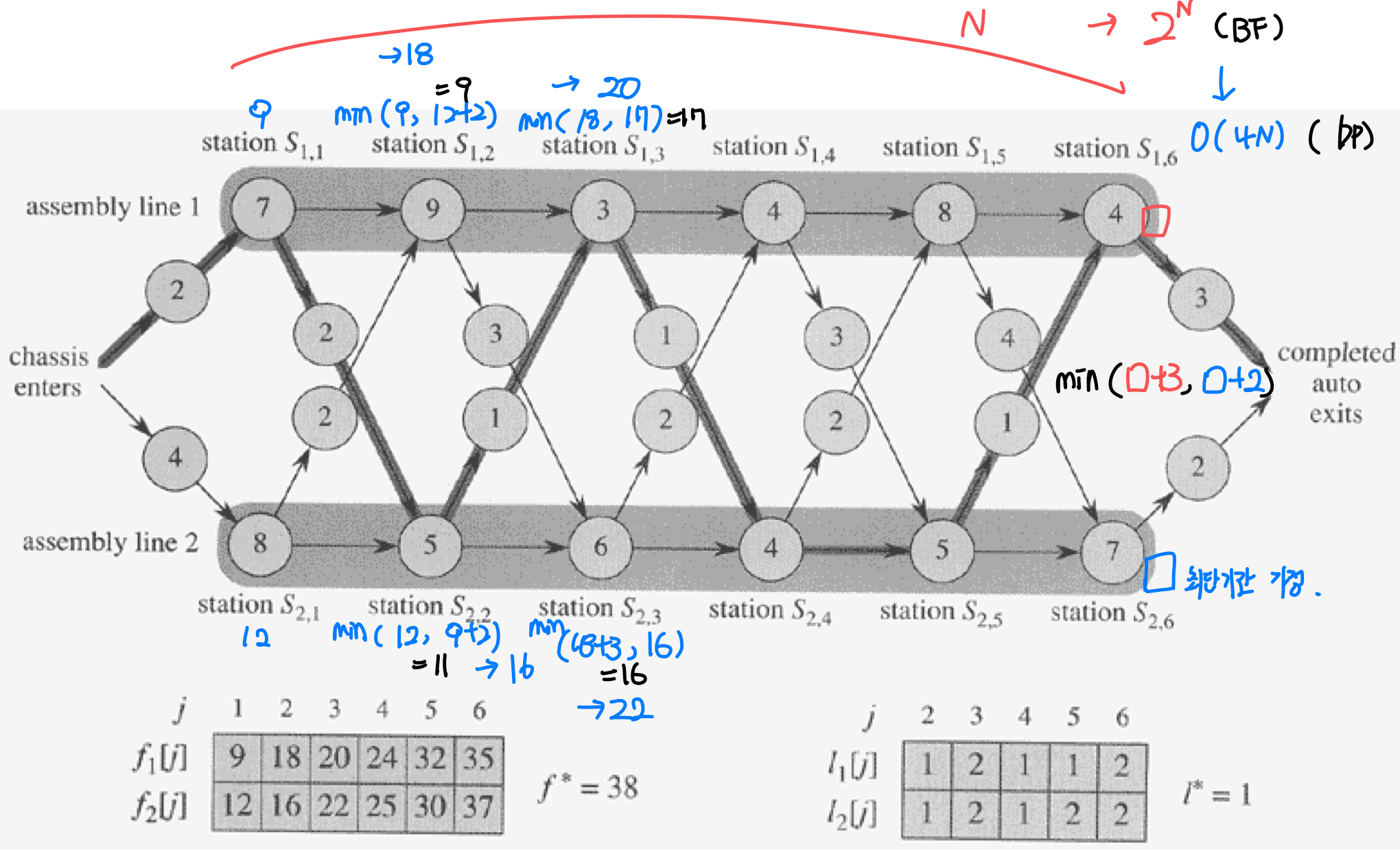
Dynamic Programming
- Step1. 공장을 통과하는 가장 빠른 길의 구조
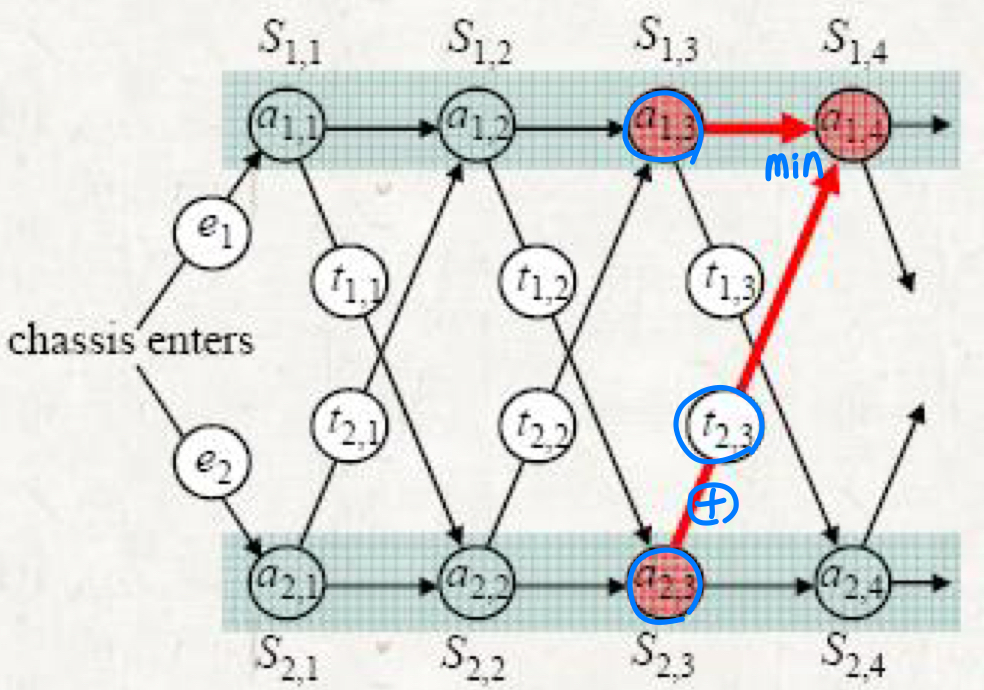
- S(i, j) = min {S(1, j-1), S(2, j-1)}
- Step2. 재귀적으로 문제 해결
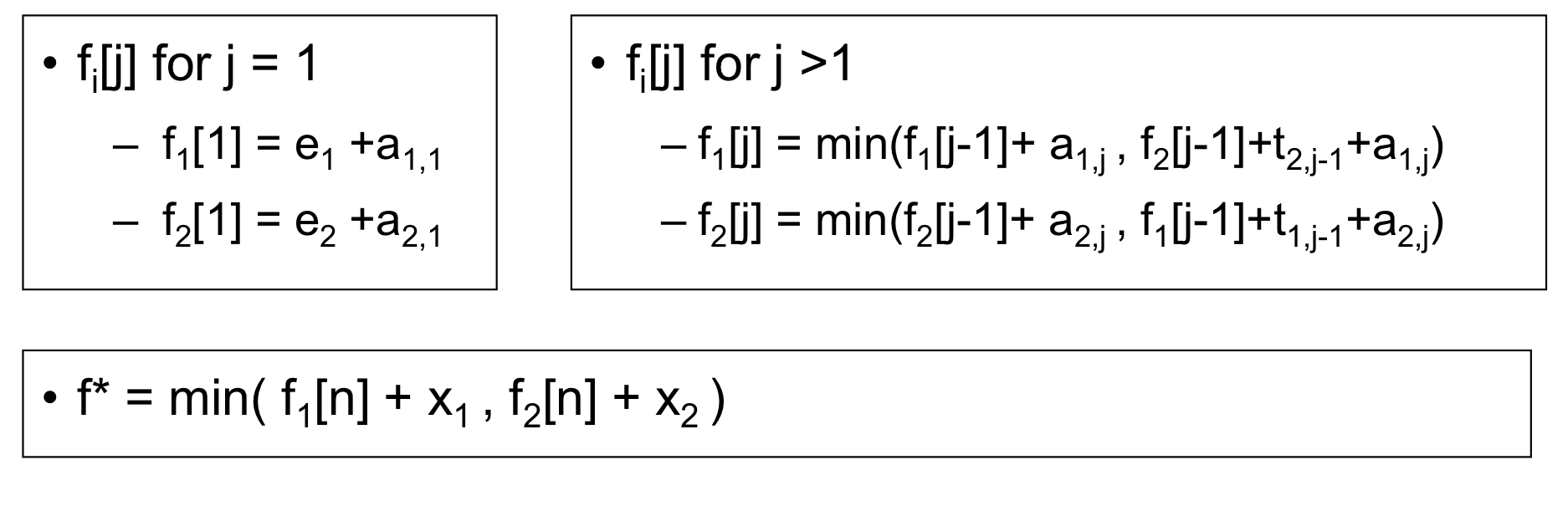
- Step3. 가장 빠른 시간을 계산함
- Simple Recursive Solution
- 실행 시간 = Θ(2^n)
- Dynamic Programming
- 실행 시간 = Θ(n)
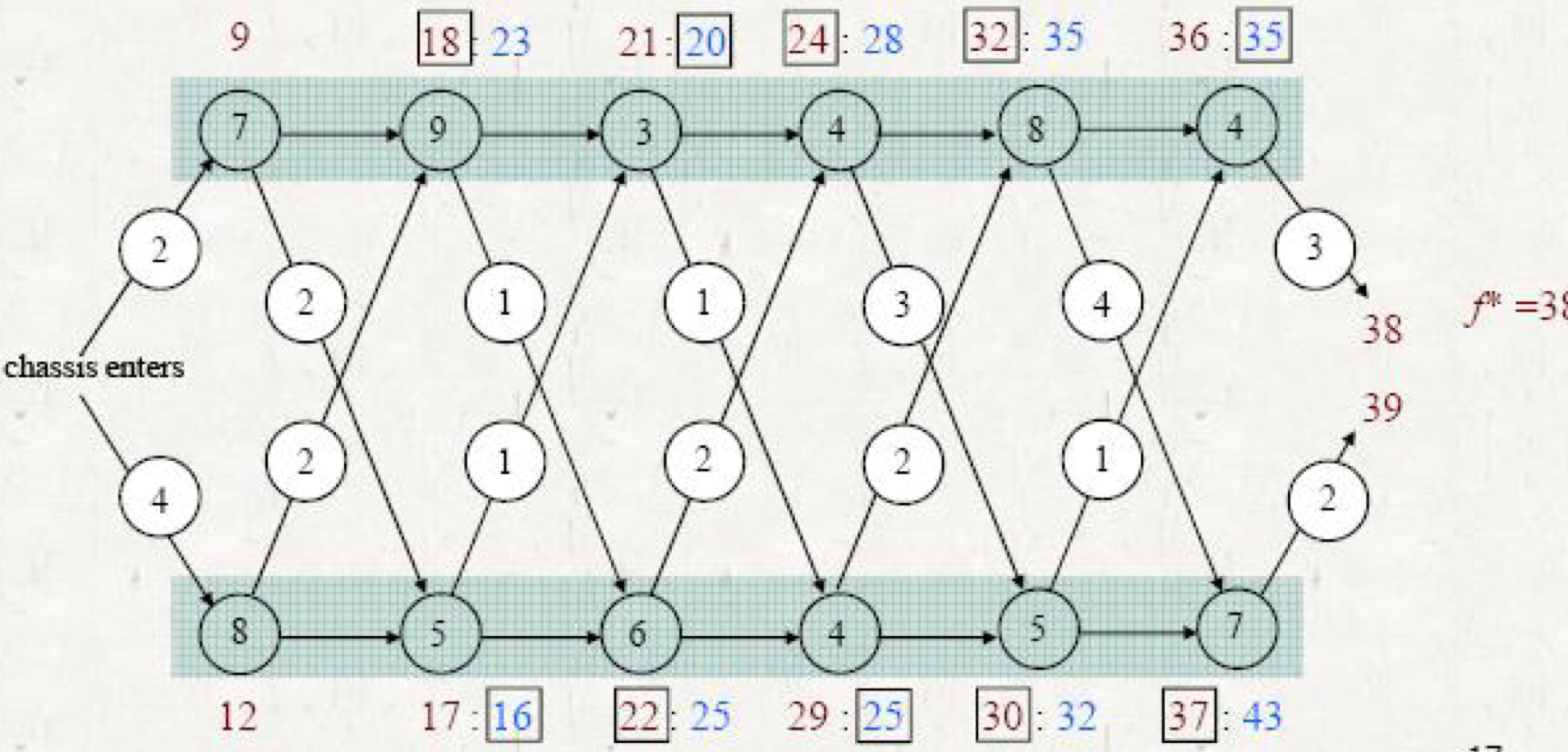
- 실행 시간 = Θ(n)
- Simple Recursive Solution
- Step4. 공장을 통과하는 가장 빠른 길을 건설하기
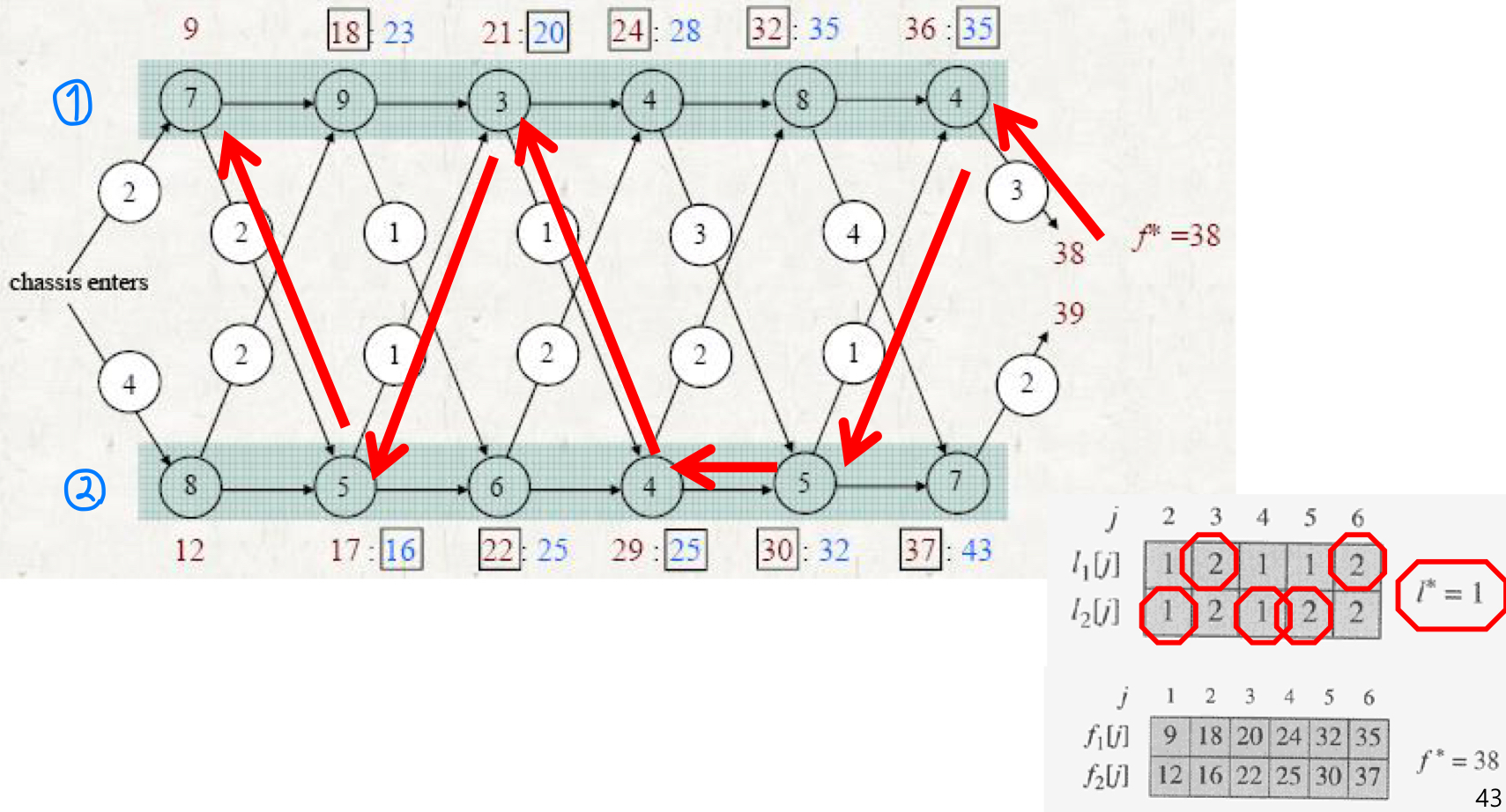
행렬 체인 곱셈(Matrix-chain multiplication)
- 행렬을 곱하는 방법의 수 == 행렬을 완전히 괄호로 묶는 방법의 수
- ex) A1A2A3 -> A1(A2A3), (A1A2)A3
- 곱셈의 순서
- 곱셈의 순서는 다음 값을 변경하지 않음
- 행렬 곱셈은 연관성이 있기 때문에 생성됩니다.
- 예를 들어 왼쪽 곱셈이 먼저 수행되는지 또는 오른쪽 곱셈이 먼저 수행되는 것은 중요하지 않음
- (A1·A2) · A3 = A1· (A2·A3)
- 그러나 곱셈의 순서는 곱셈을 계산하는 데 필요한 스칼라 곱셈의 수에 영향을 미침
- 두 행렬 A 및 B 곱셈
- A의 열 수는 B의 행 수와 같아야 함
- A가 p×q 행렬이고 B가 q×r 행렬이면 결과 행렬은 p×r 행렬임
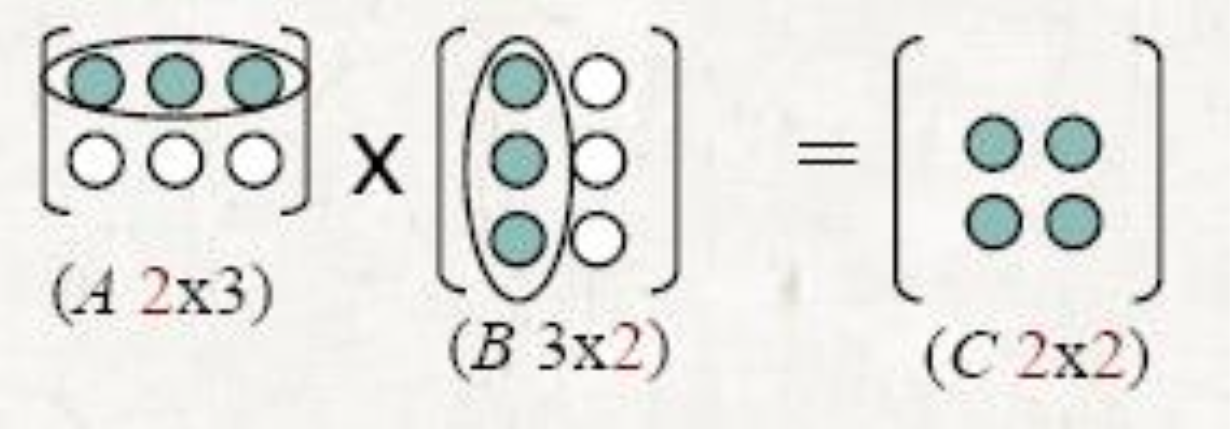
- A와 B를 곱할 스칼라 곱셈의 수
- pr 요소를 계산하고 각 요소를 계산하려면 q 스칼라 곱셈이 필요하기 때문에 pqr임
- 곱셈의 순서는 스칼라 곱셈의 수에 영향을 미침
- Computing A1A2A3 where A1: 100×10 A2: 10×50 A3 : 50×5
- (A1A2)A3
• (A1A2) = 1001050 = 50,000, (100×50) A3 = 100505 = 25,000
=> 50,000 + 25,000 = 75,000 – A1(A2A3)
• (A2A3) = 10505 =2,500, A1(10×5) = 100105 = 5,000
=> 2,500 + 5,000 = 7,500 - Computing A1(A2A3) is 10 times faster.
- 행렬 A가 pi-1 × pi 차원을 갖는 체인 A1, A2, ..., Anof n 행렬이 주어지면, 곱을 계산하기 위한 스칼라 곱셈을 최소화하는 행렬 곱셈 순서를 찾음
- 즉, 스칼라 곱을 최소화하는 행렬의 곱을 완전히 괄호로 묶는 것
• 예를 들어 제품 A1 A2 A3 A4의 경우 전체 괄호는 (A1 A2) A3) A4
Brute-force approach
- 가능한 모든 괄호를 열거합니다.
- 각 괄호의 스칼라 곱셈 수를 계산합니다.
- 최소 수의 스칼라 곱셈이 필요한 괄호를 선택합니다.

Dynamic Programming
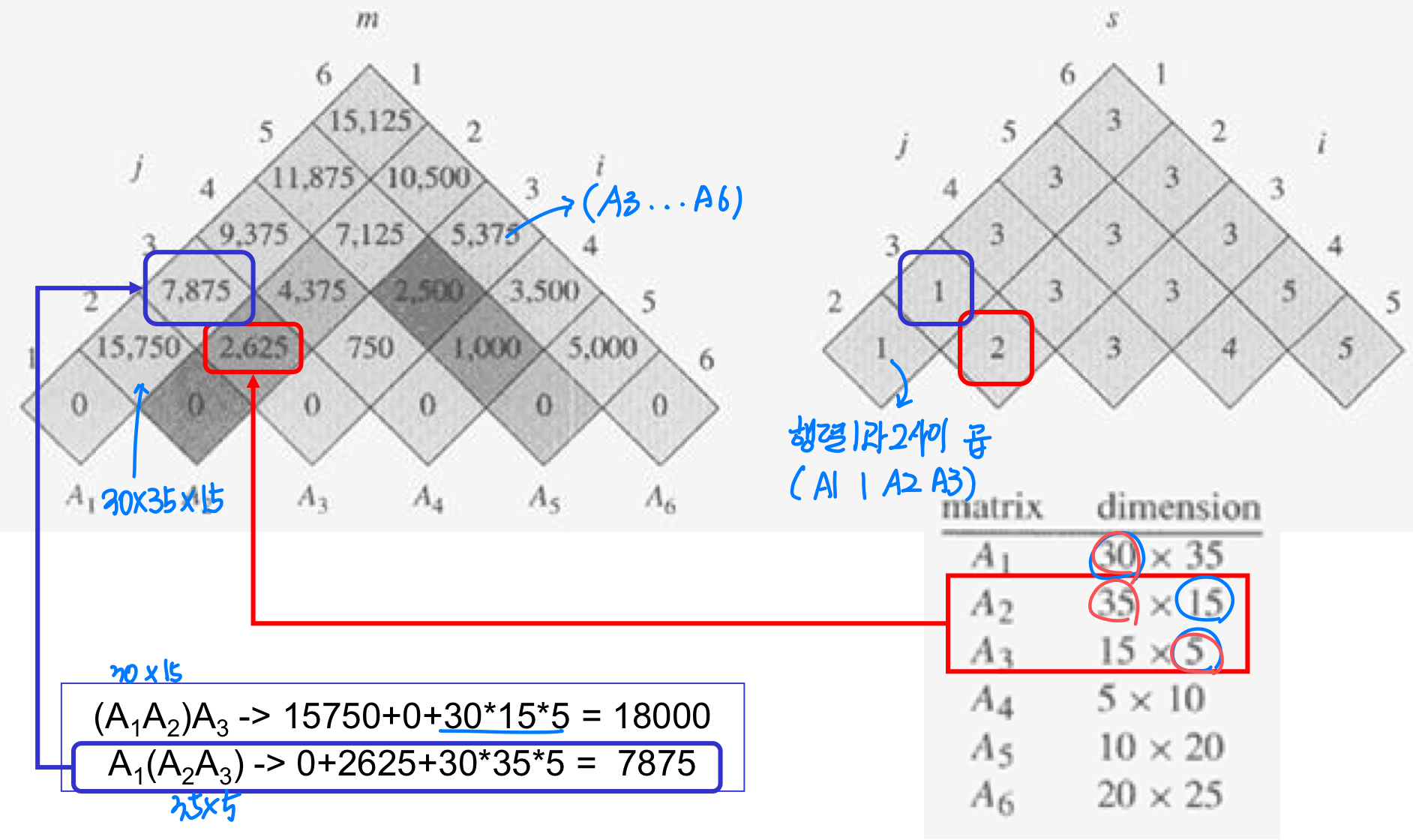
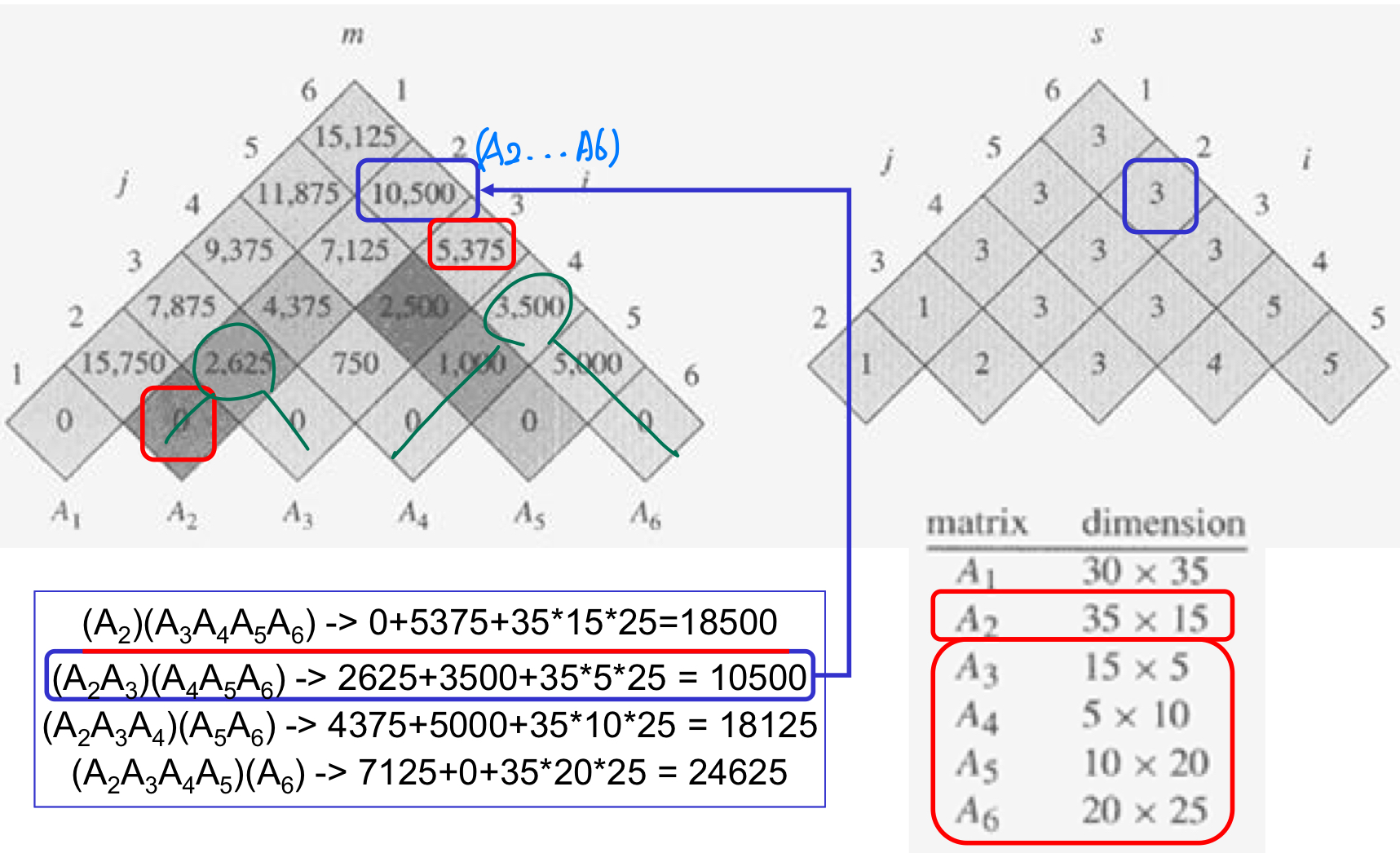
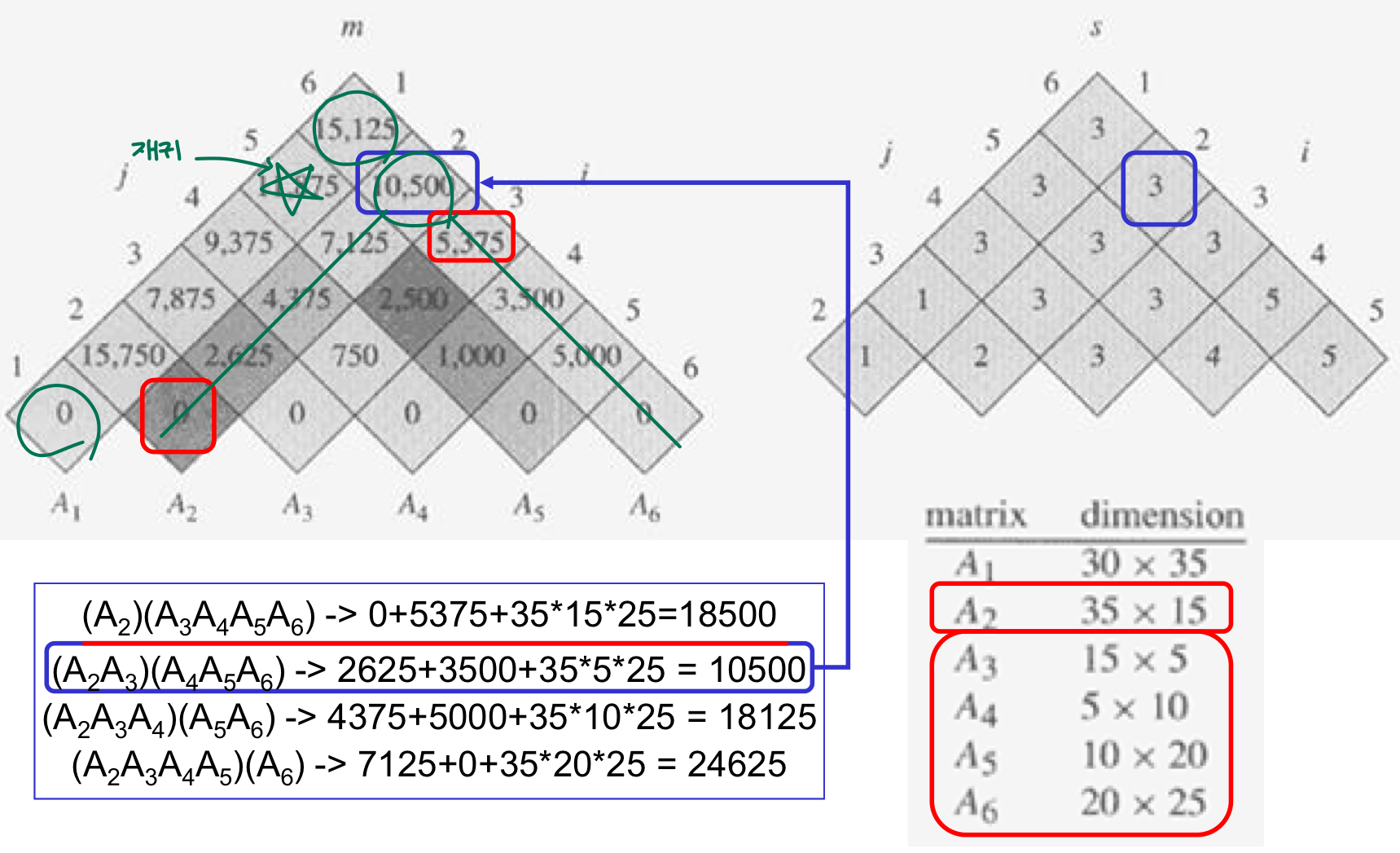
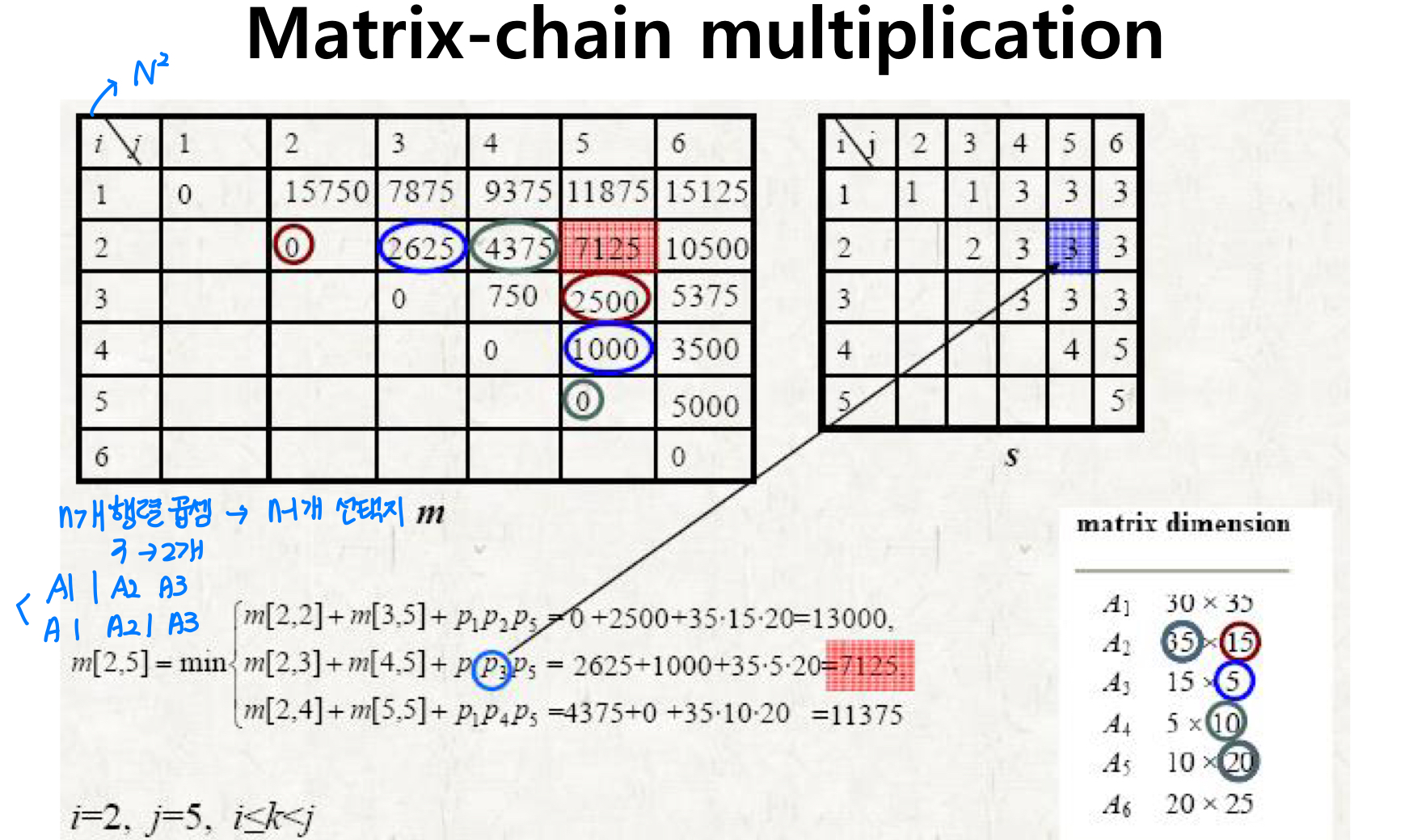
- optimal substructure

- matrix Ai: pi-1 x pi
- Ai..k Ak+1..j는 pi-1 pk pj 스칼라 곱셈을 사용
- s[i,j]는 최적 솔루션을 추적하기 위한 최적 k를 저장

- 실행 시간
- 총 O(n^3)
- subproblems: Θ(n^2)
- each subproblem: O(n)
- 총 O(n^3)
- 공간 소비
- Θ(n^2) space

- Θ(n^2) space
