
재귀적 해법: Top-down
- 엄청난 중복 호출이 존재함
Dynamic Programming
- 다이내믹 프로그래밍은 문제를 하위 문제로 나누어 해결하는 방법이다.
- 만약 하위 문제들이 서로 독립적이라면, 분할 정복 방법을 사용하게 된다.
- 하지만, 만약 하위 문제들이 독립적이지 않다면, 다이내믹 프로그래밍을 사용하게 된다.
- 다이내믹 프로그래밍 알고리즘은 모든 하위 문제들을 한 번씩만 해결하고 그 결과를 테이블에 저장하여 재사용한다.
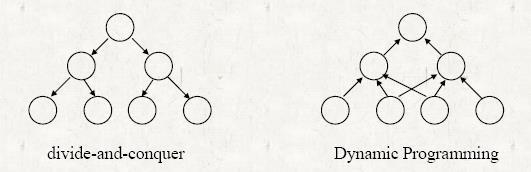
- 다이내믹 프로그래밍은 일반적으로 최적화 문제를 해결하는
데 사용된다.
• 최적화 문제(Optimization problems)
– 최적화 문제란, 많은 가능한 해결책 중에서 각 해결책마다 값이 존재하며, 이 중에서 최적 (최소 또는 최대) 값을 가지는 해결책을 찾는 문제이다.
– 이러한 해결책을 문제의 최적해(optimal solution)라고 한다.- 최단 경로 문제(Shortest path example)는 대표적인 예시 중 하나
- 다이나믹 프로그래밍 알고리즘 개발 단계
- 최적해의 구조를 정의한다.
- 최적해의 값을 재귀적으로 정의한다.
- 최적해의 값을 바텀업 방식으로 계산한다.
- 계산된 정보를 기반으로 최적해를 구성한다.
- DP 적용 요건
• Optimal substructure
– 큰 문제의 최적 솔루션에 작은 문제의 최적 솔루션이 포함됨
• Overlapping recursive calls
– 재귀적 해법으로 풀면 같은 문제에 대한 재귀호출이 심하게 중복됨
DP가 그 해결책!
Basic Example
- Coin-row problem
- 길이가 n인 동전 줄이 있으며, 각 동전의 가치는 양의 정수 c1, c2, ..., cn이다.
- 인접한 두 동전은 선택할 수 없는 제약 조건을 만족하면서, 최대한 많은 금액을 선택한다.

![]
(https://velog.velcdn.com/images/ssonzm/post/30f10d88-d794-4248-9e1e-986b972b702b/image.png)
