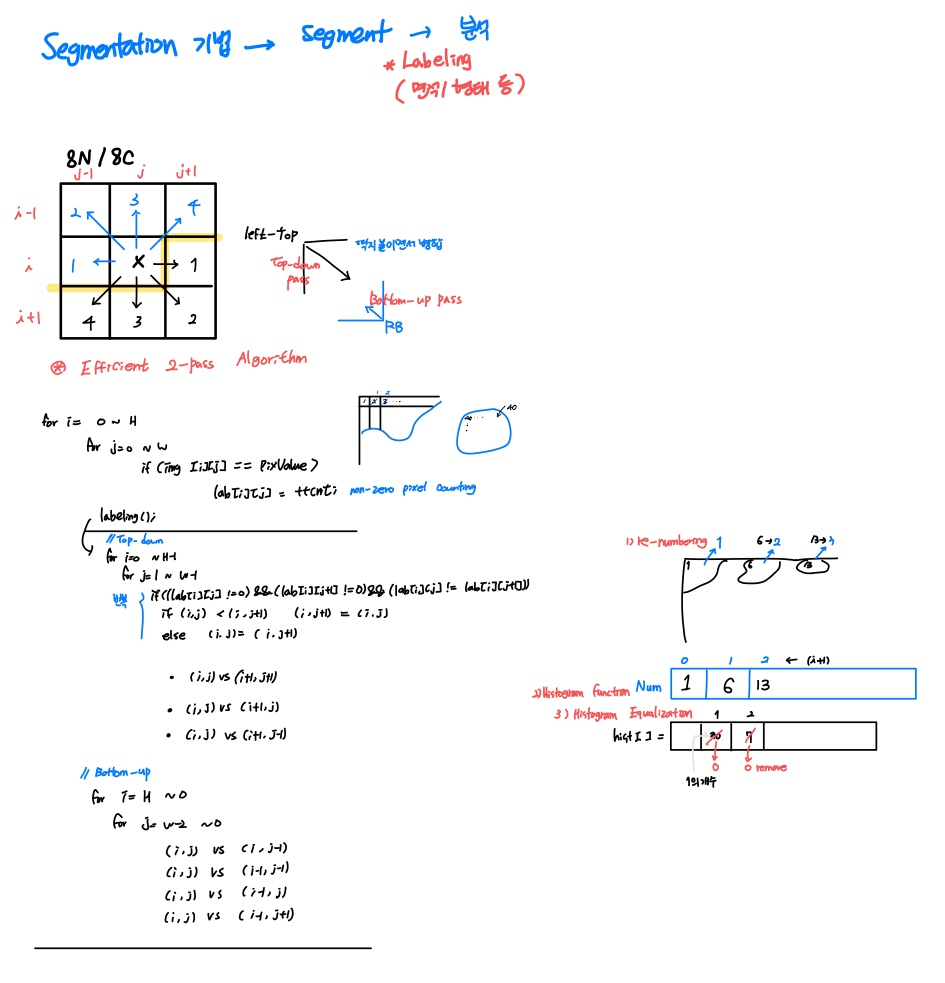
영상분할
- 이미지 분할의 목표는 입력 이미지를 동질성 및 연결 조건을 충족하는 분리된 하위 영역으로 분할하는 것이다.
- Homogeneity(균질성): 모든 픽셀이 균질한 경우 영역
- Connectivity(연결성): 두 픽셀 사이에 연결된 경로가 있는 경우 영역
- 정확히 말하면, 이미지 R의 분할은 다음 조건을 만족하는 R1, R2, …, RN의 분리된 하위 영역으로 분할하는 것이다.
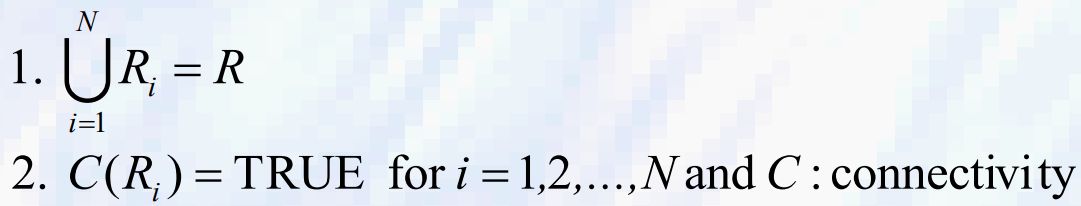
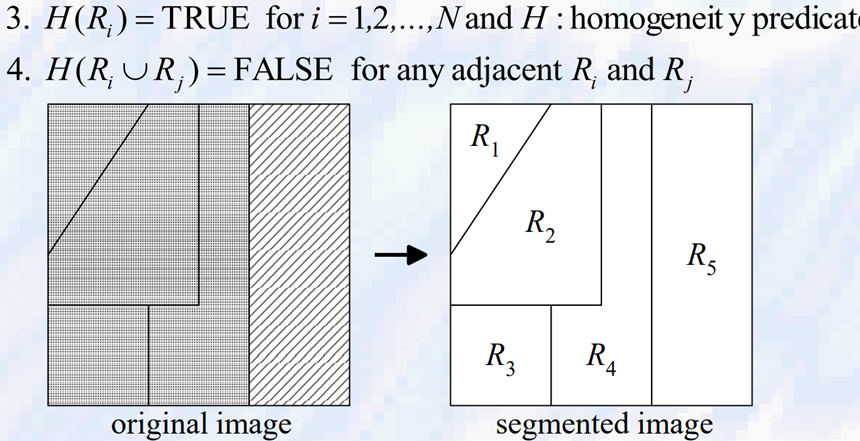
- R1과 R4는 Homogeneity는 만족하지만 두 영역 사이에 어떠한 연결된 경로가 없다 -> Connecivity 만족하지 않음
segmentation 주요 접근 방법
1. Thresholding
2. edge-based method
3. region-based method
Thresholinding
- 회색 수준 임계값은 가장 간단한 분할 프로세스이다. 임곗값은 계산적으로 저렴하고 빠르다.
- 이것은 가장 오래된 분할 방법이며 여전히 단순한 응용 프로그램에서 널리 사용된다.
- 특수 하드웨어를 사용하여 실시간으로 쉽게 임계값을 설정할 수 있다.
- 임계값은 다음과 같이 입력 이미지 u를 출력 이진 이미지 v로 변환하는 것이다.
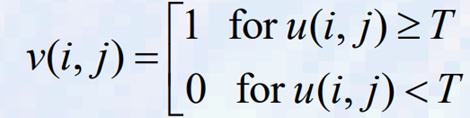
- 여기서 T는 임계값, 객체 픽셀의 경우 v(i,j)=1, 배경 픽셀의 경우 v(i,j)=0 (또는 그 반대)
Threshold Selection: 오류 확률 최소화
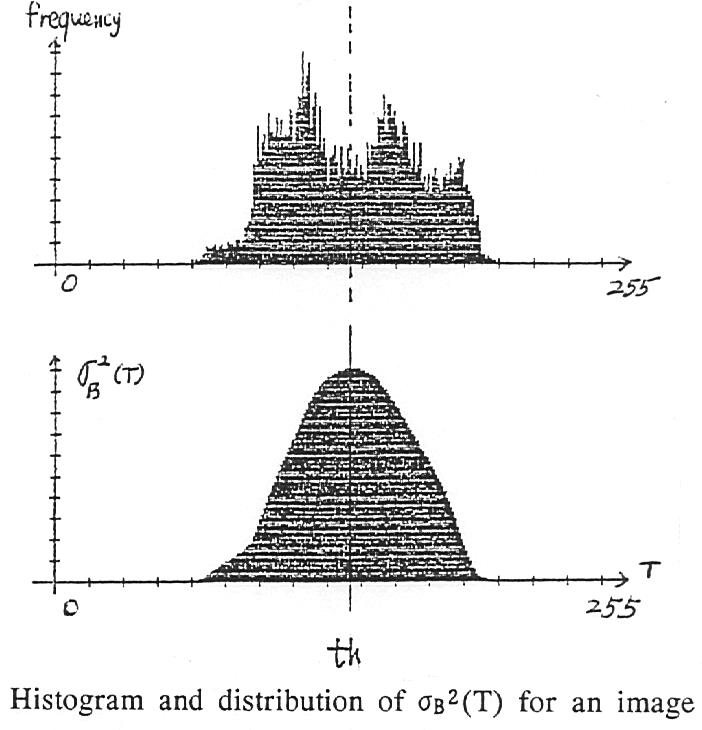
- 임계값 선택의 일반적인 방법은 히스토그램 모양 분석을 기반으로 한다.
- 이미지가 배경의 회색 수준과 거의 동일한 회색 수준의 개체로 구성된 경우 결과 히스토그램은 bimodal이다.
- 다음 그림과 같이 객체의 픽셀은 피크 중 하나를 형성하고 배경의 픽셀은 두 번째 피크를 형성한다.
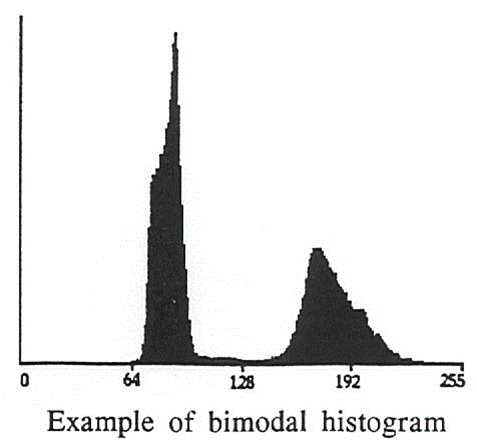
- 선택한 임계값은 최소 분할 오류 요구 사항을 충족해야 한다.
- 언급된 두 최대값 사이에 최소 히스토그램 값(σ)을 갖는 회색 레벨로 임계값을 결정하는 것은 직관적으로 의미가 있다.

- 임계값은 총 오류 확률을 최소화하는 회색 값으로 선택된다.

- 여기서 mi는 배경 또는 객체 픽셀을 나타내고, di는 각 결정을 나타낸다.
- 조건부 확률의 사용에 의해
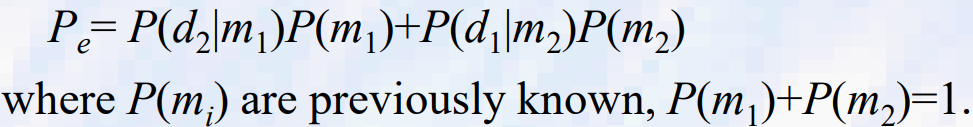
2.배경 영역과 객체 영역에 대한 각 확률 밀도 함수 pi(x)가 평균 δi 및 분산 δi^2와 단모달이라고 가정합니다.
- 즉, 이미지의 확률 밀도 함수가 바이모달이라고 가정합니다.
- δ1과 δ2의 경우, 오분류의 확률은 다음과 같이 주어진다
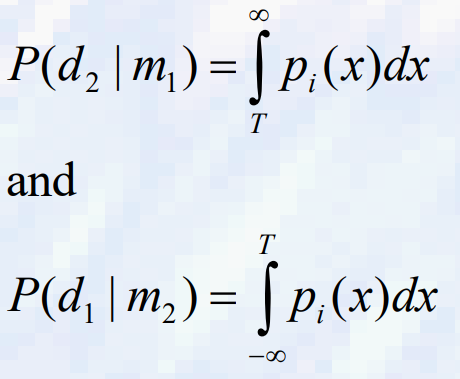
- 총 오류 확률이 최소인 임계값을 찾기 위해서는 T와 관련하여 미분 Pe(T)가 필요하며 결과를 0으로 동일시해야 한다.
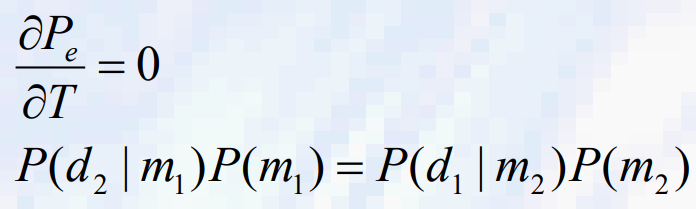
- 각 확률 밀도 함수 pi(x)가 가우스라고 가정합니다. 위에서 언급한 방정식은 다음과 같이 단순화될 수 있다.
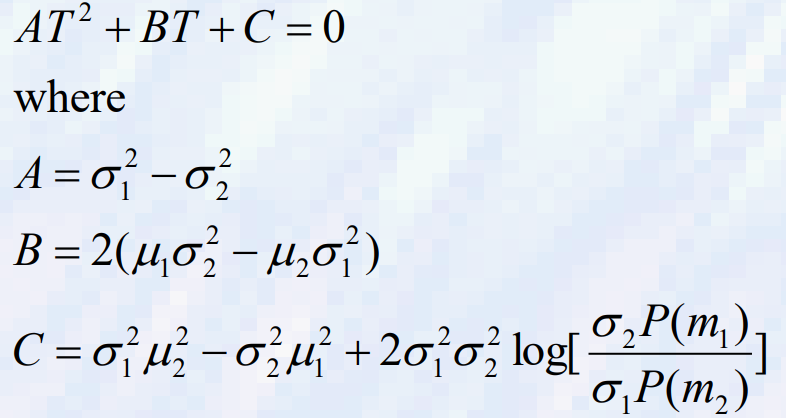
- 분산이 같다면 최적의 단일 임계값은 이와 같다.
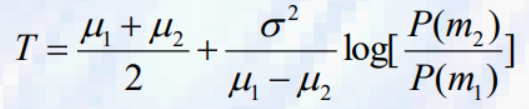
- 이전 확률이 P(m1)=P(m2)인 경우 최적 임계값은 평균의 평균이다.
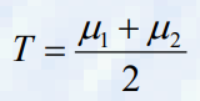
- 최적 임계값의 결정은 알려진 형태의 다른 단모달 밀도에 대해 유사하게 달성될 수 있다.
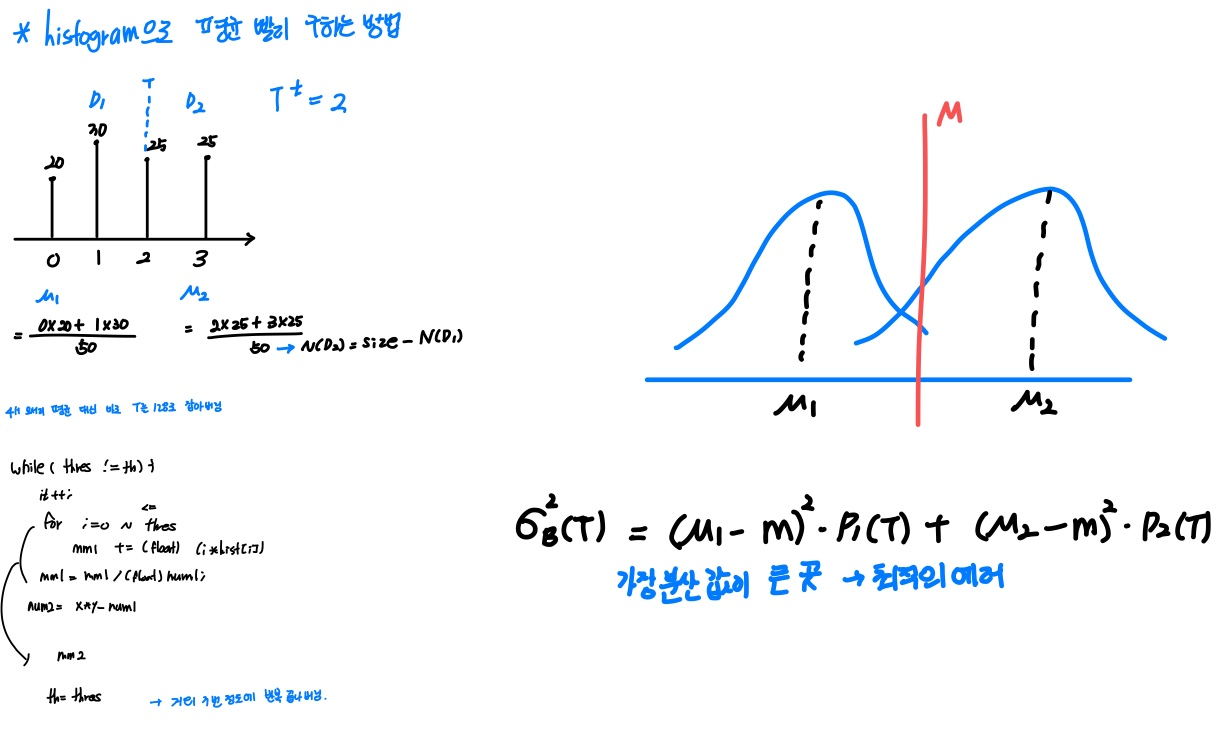
Iterative Threshold selection
- 이 방법은 두 가지 주요 회색 레벨의 영역이 영상에 있다고 가정합니다. 이 알고리즘은 반복적이며 보통 4~10회 반복하면 충분하다.
- 알고리즘:
a. 개체의 정확한 위치에 대한 지식이 없다고 가정하면 첫 번째 근사치로 이미지의 네 모서리에는 배경 픽셀만 포함되고 나머지 모서리에는 개체 픽셀이 포함된다.
b. t단계에서 u1^t와 u2^t를 평균 배경 및 객체 그레이 레벨로 계산한다. 여기서 t단계에서 배경 및 객체로의 분할은 이전 단계에서 결정된 임계값 T^t에 의해 정의된다.
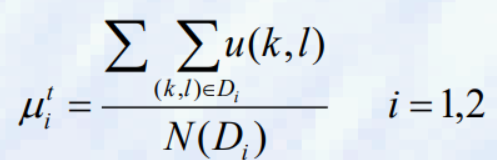
여기서 Di는 mi 픽셀들의 영역을 의미하고, N(Di)는 영역 내의 픽셀들의 수를 의미한다.
c.
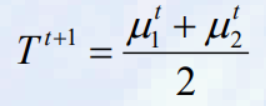
d. T^t+1= T^t이면 중지하고, 그렇지 않으면 b 단계로 돌아간다. - u1^t와 u2^t를 히스토그램 기반으로 계산하면 더 효율적이다.
Threshold selection: 클래스 간 분산 최대화[Otsu]
- 임계값은 다음과 같이 정의된 클래스 간 분산을 최대화하는 회색 값으로 선택된다.
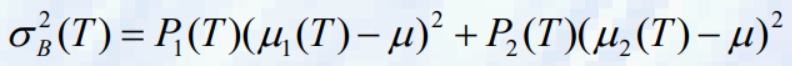
- 여기서 u는 총 픽셀의 평균이고, ui^t(T)는 T로 정의된 각 클래스의 평균이며, Pi(T)는 각 클래스의 상대 주파수입니다. 방정식은 다음과 같이 다시 쓸 수 있다.
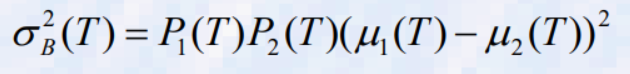
- σB^2(T)에 대한 최대 T를 결정하기 위해서는 모든 T에 대해 ui(T)와 Pi(T)의 양이 결정되어야 한다. 그러나 각 T에 대해 독립적으로 수행할 필요는 없습니다. 확률은 다음과 같이 재귀적으로 계산할 수 있다
P1(T) = P1(T-1) + P(T) and
P2(T) = 1 - P1(T)
- 여기서 초기 값은 P1(0)=P(0)이고 P는 총 픽셀에 대한 확률 분포를 나타낸다. 두 클래스 평균은 다음과 같이 재귀적으로 계산될 수 있다.
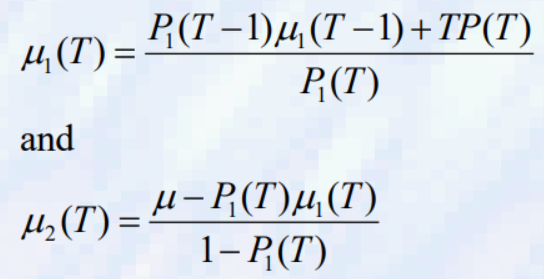
- The distribution of σB^2(T),
Threshold selection: 히스토그램 엔트로피 최대화 [Kapur]
- 임계값은 다음과 같이 정의된 각 클래스 엔트로피의 합을 최대화하는 회색 값으로 선택된다.
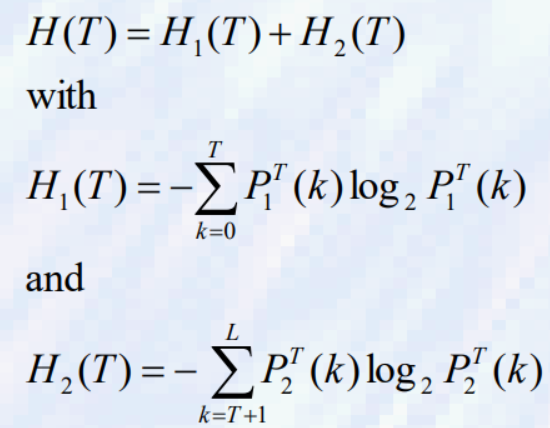
- 여기서 L은 최대 회색 레벨과 Pi를 나타낸다.
- T(k)는 T로 정의된 클래스 i의 픽셀들의 확률 분포이다.
Edge-based segmentation
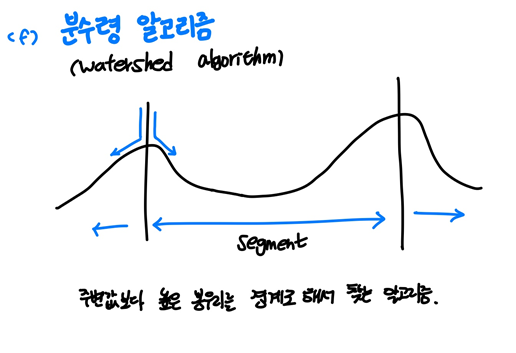
Region-based segmentation