
Elements of DP
- 가중치가 없는 최단 단순 경로 문제
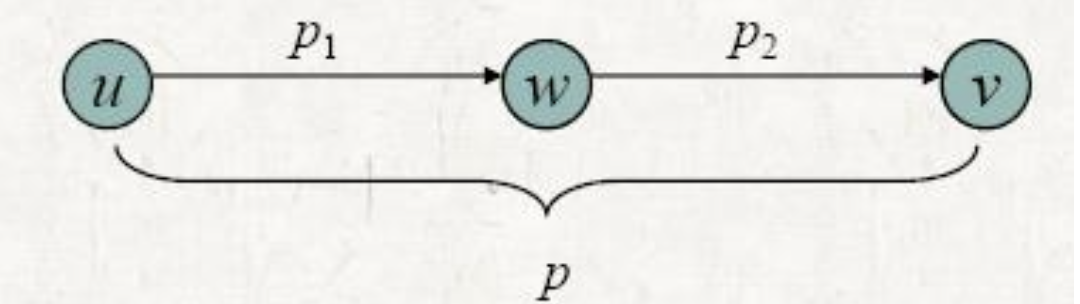
- 가중치가 없는 최장 단순 경로 문제
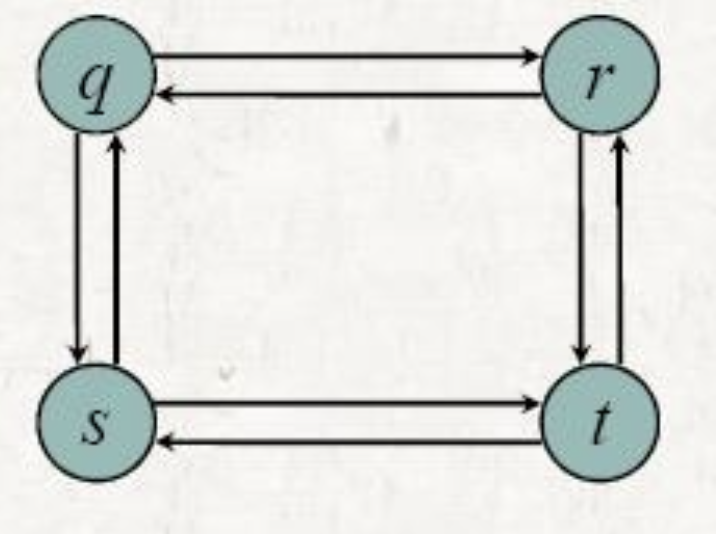
• 최적의 하부구조를 가지고 있습니까?
• 하위 문제는 독립적입니까? – q -> t ?= q -> r + r -> t
• NP-complete
중복 하위 문제
- 재귀 알고리즘이 동일한 문제를 반복적으로 재검토할 때
다시 말하면, 최적화 문제는 중복된 하위 문제를 가지고 있습니다.
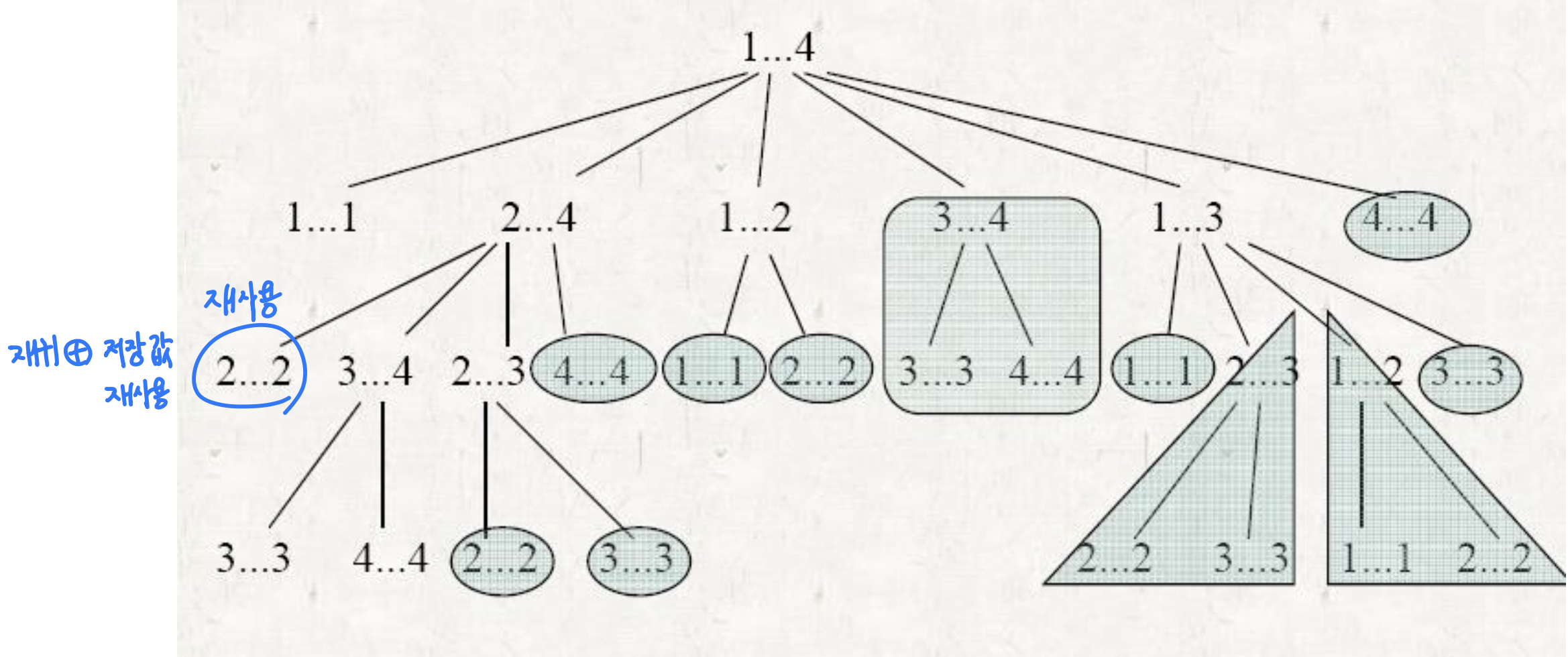
Memorization
- 재귀적인 해결책이지만 각 하위 문제를 한 번만 해결합니다.
- 테이블을 재귀적인 방식으로 채웁니다.
- 대부분의 경우 동적 프로그래밍보다 느립니다.
- 하위 문제의 일부만 해결할 때 유용합니다.
Longest common subsequence

- LCS
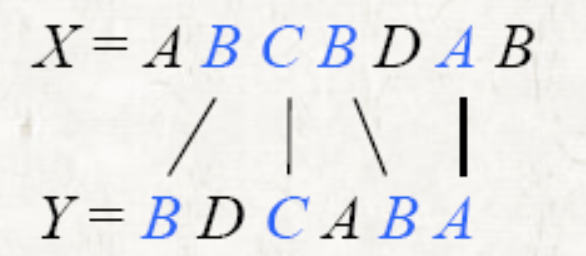
- BCBA: X, Y의 longest common subsequence
Brute force approach
- X의 모든 연속성을 열거하고 다음과 같은 경우 각 연속성을 확인합니다
이것은 또한 Y의 연속이고 가장 긴 것을 찾습니다.
-> 불가능- 2^m
Dynamic programming
- The ith prefix Xi of X is Xi=<x1,x2,...,xi>.
- If X = <A, B, C, B, D, A, B>
• X4=< A, B, C, B> • X0=<>
- 최적 하위 구조

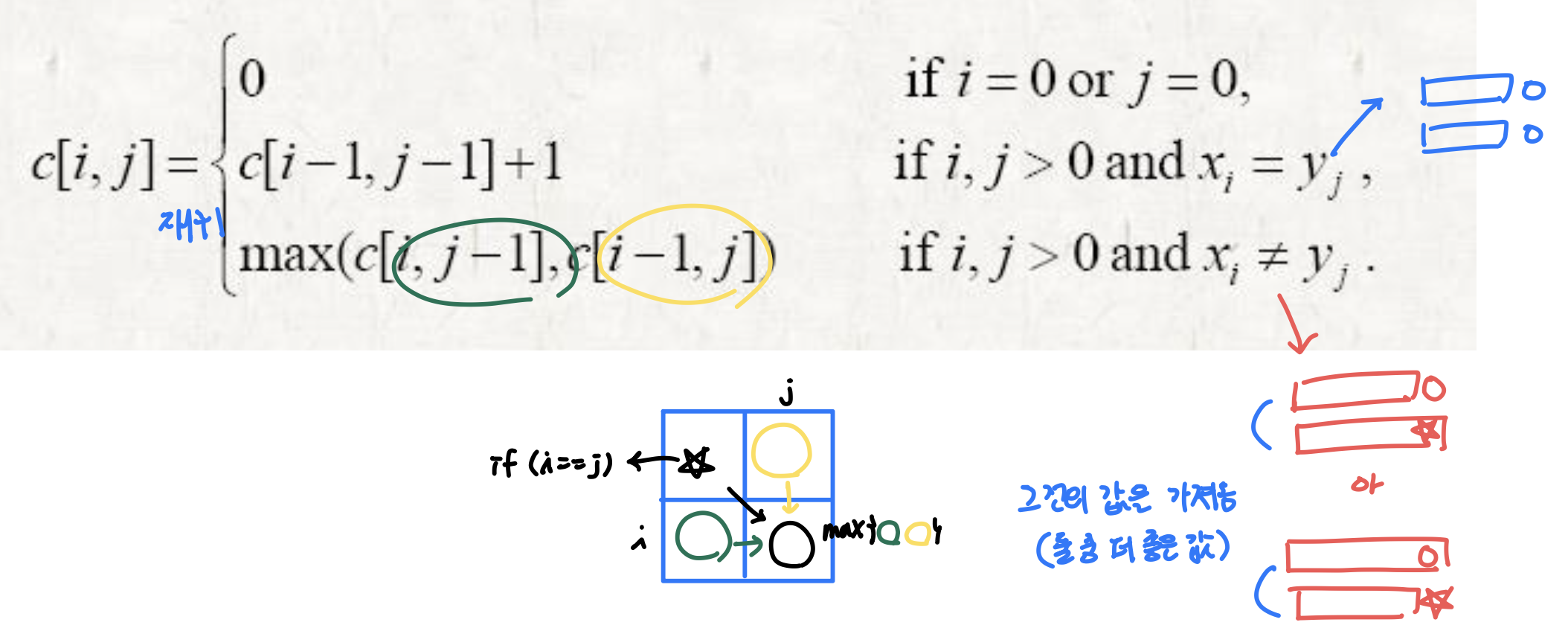
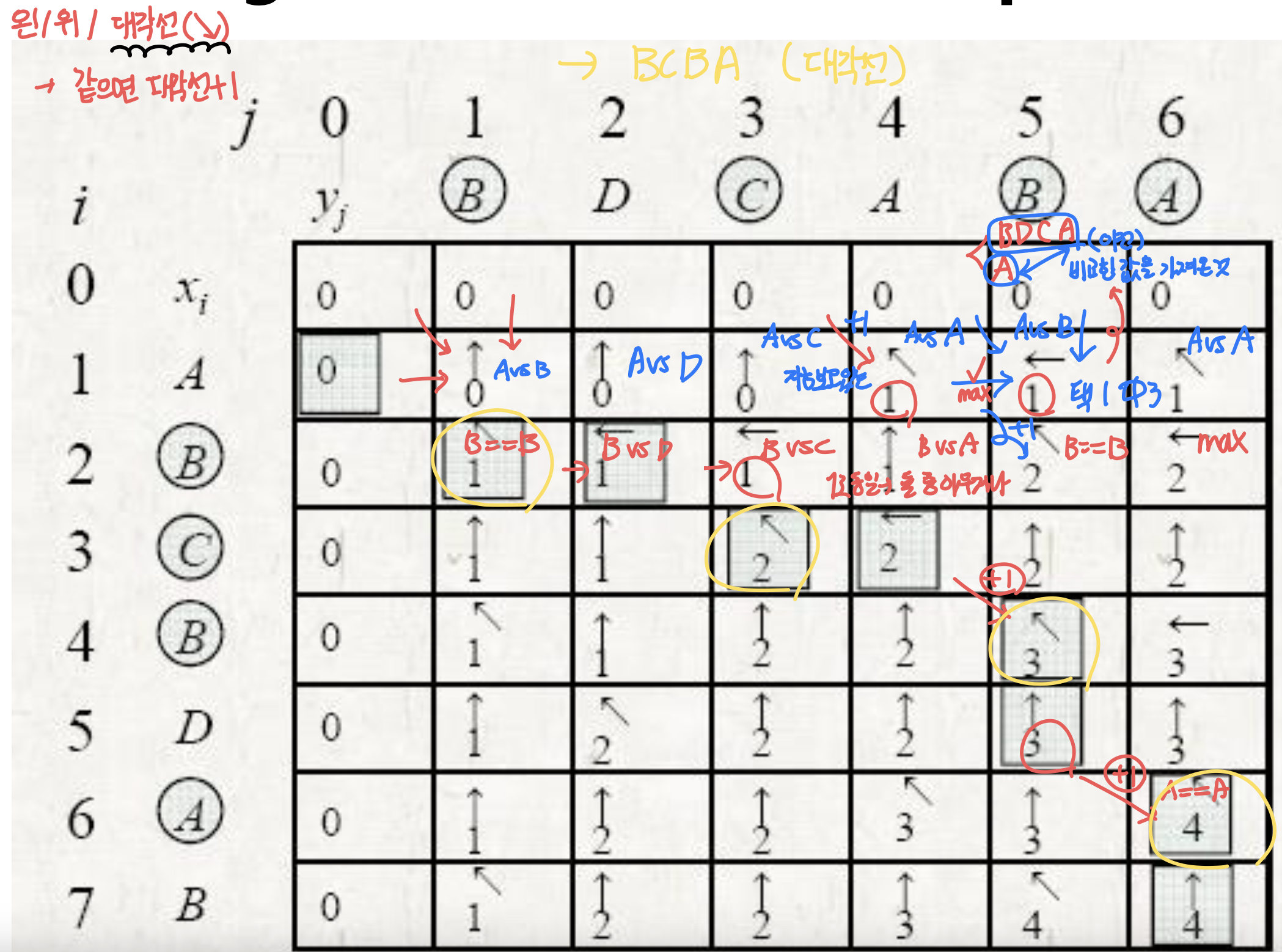
- 계산 시간: Θ(mn)
- 공간: Θ(mn)
- 공간 감소: min(m, n) + 1
- 행 이나 열 방향으로만 진행
- 바로 이전 배열만 재사용하기에 한 배열만을 통해 덮어쓰기 할 수도 있음
Minimum Edit Distance
- Levenshtein distance
- 두 시퀀스 간의 차이를 측정하기 위한 메트릭
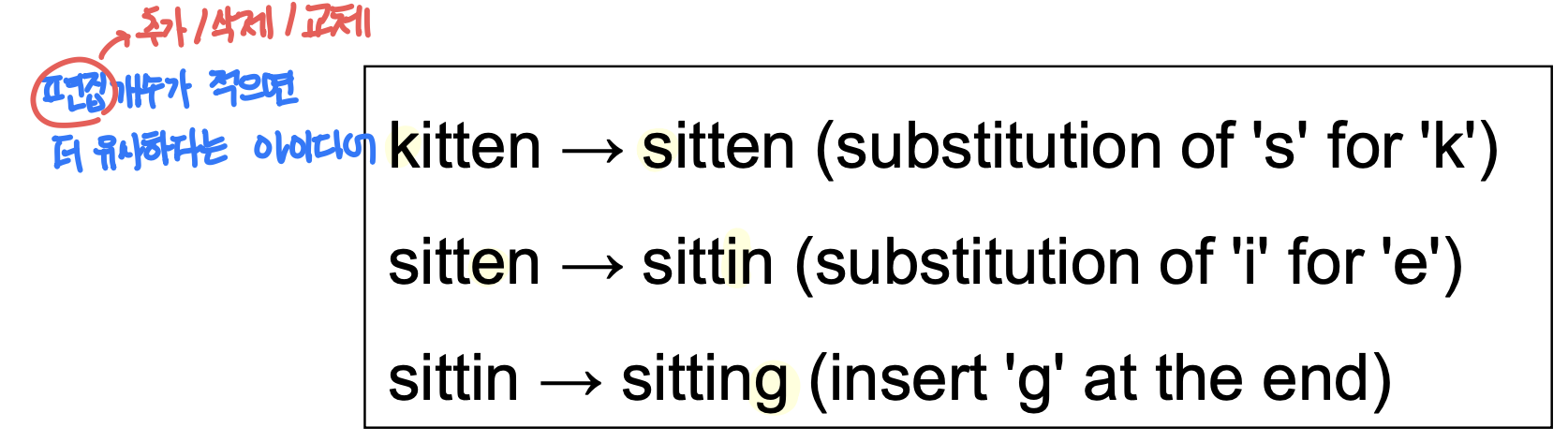
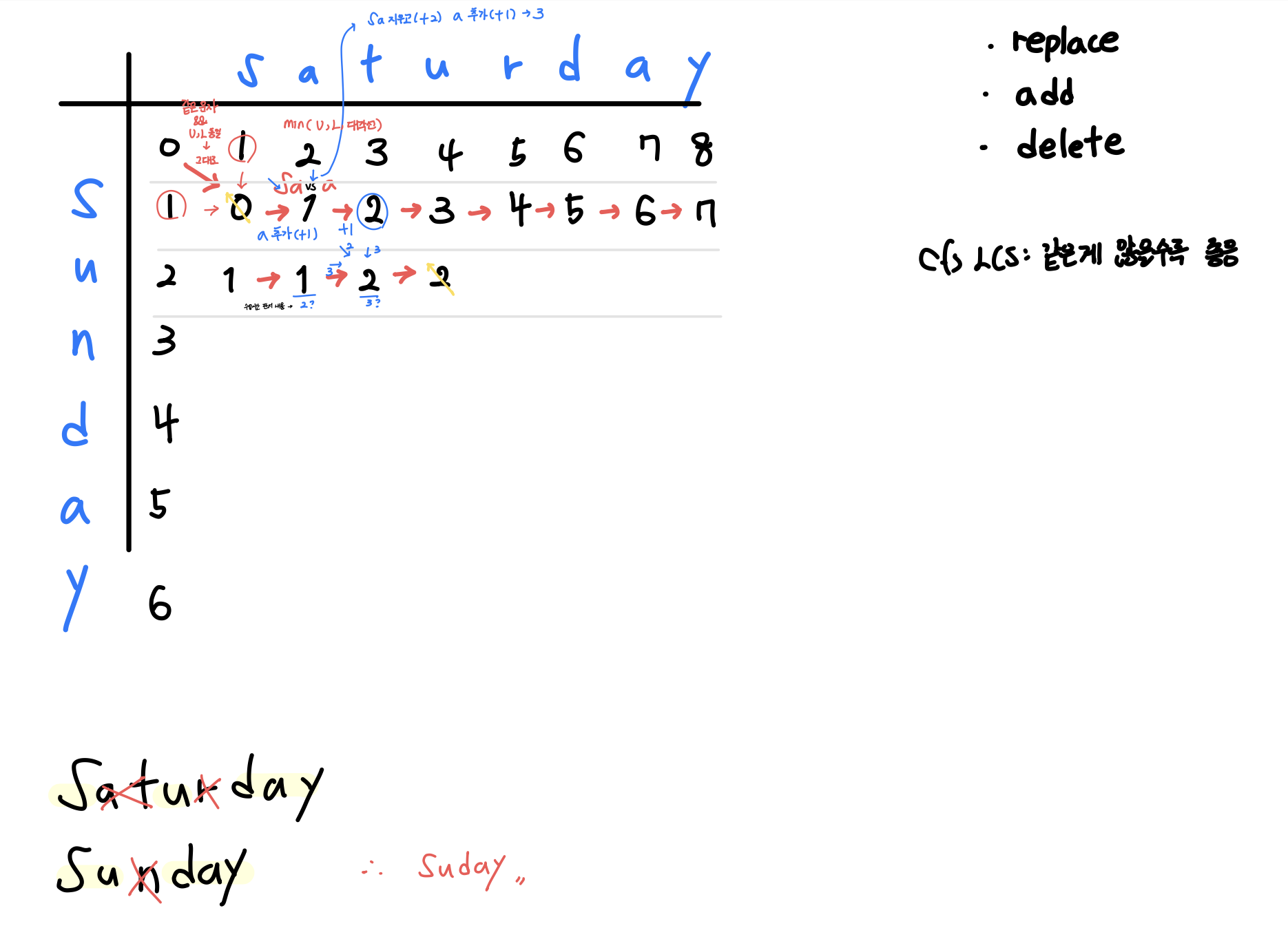
- 두 시퀀스 간의 차이를 측정하기 위한 메트릭
Optimal binary search trees
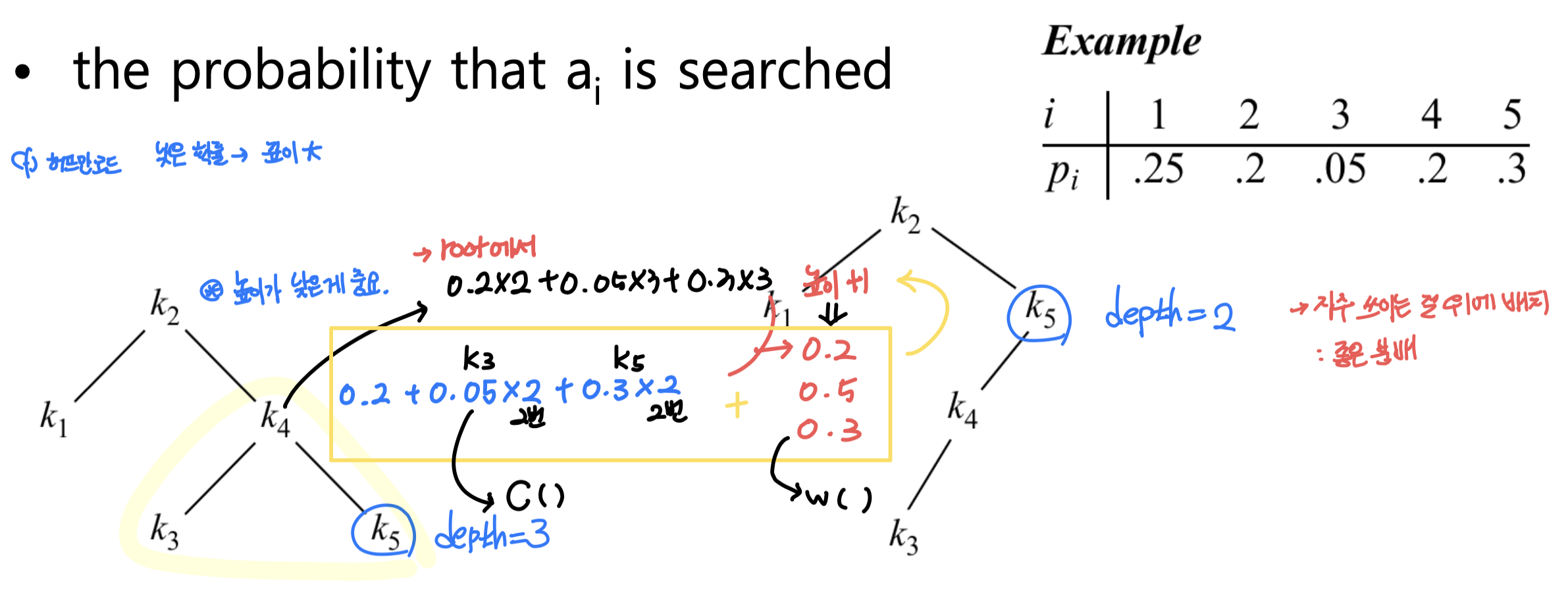

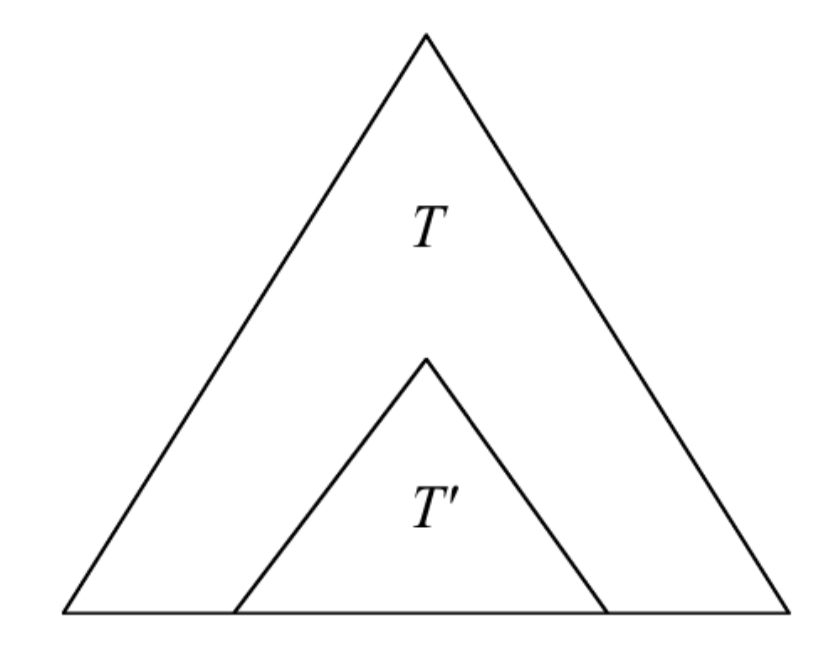
- T가 최적의 BST이고 T가 키 ki, ..., kj의 하위 트리 T'를 포함하는 경우 T'는 키 ki, ..., kj에 대한 최적의 BST여야함
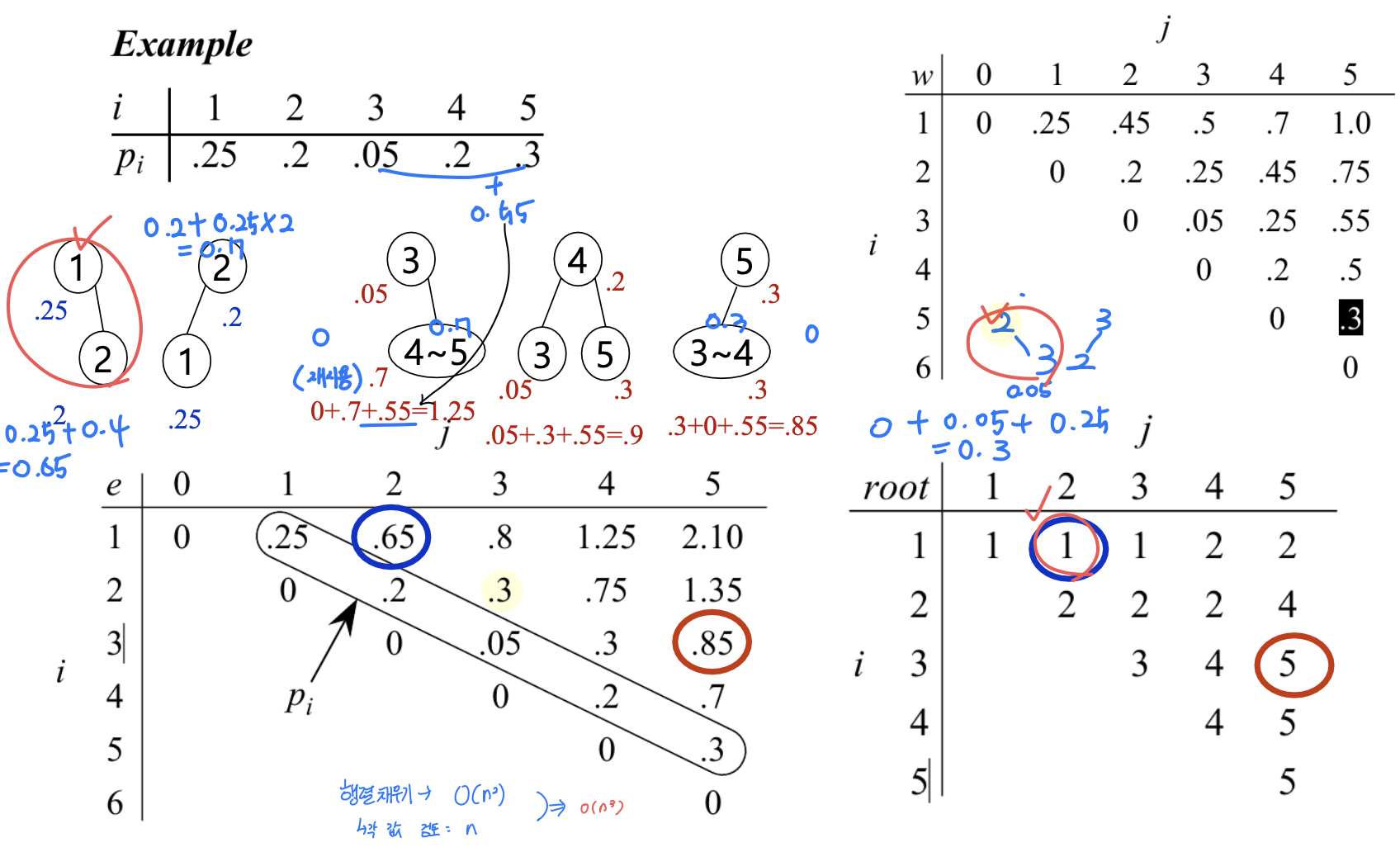
Recursive solution

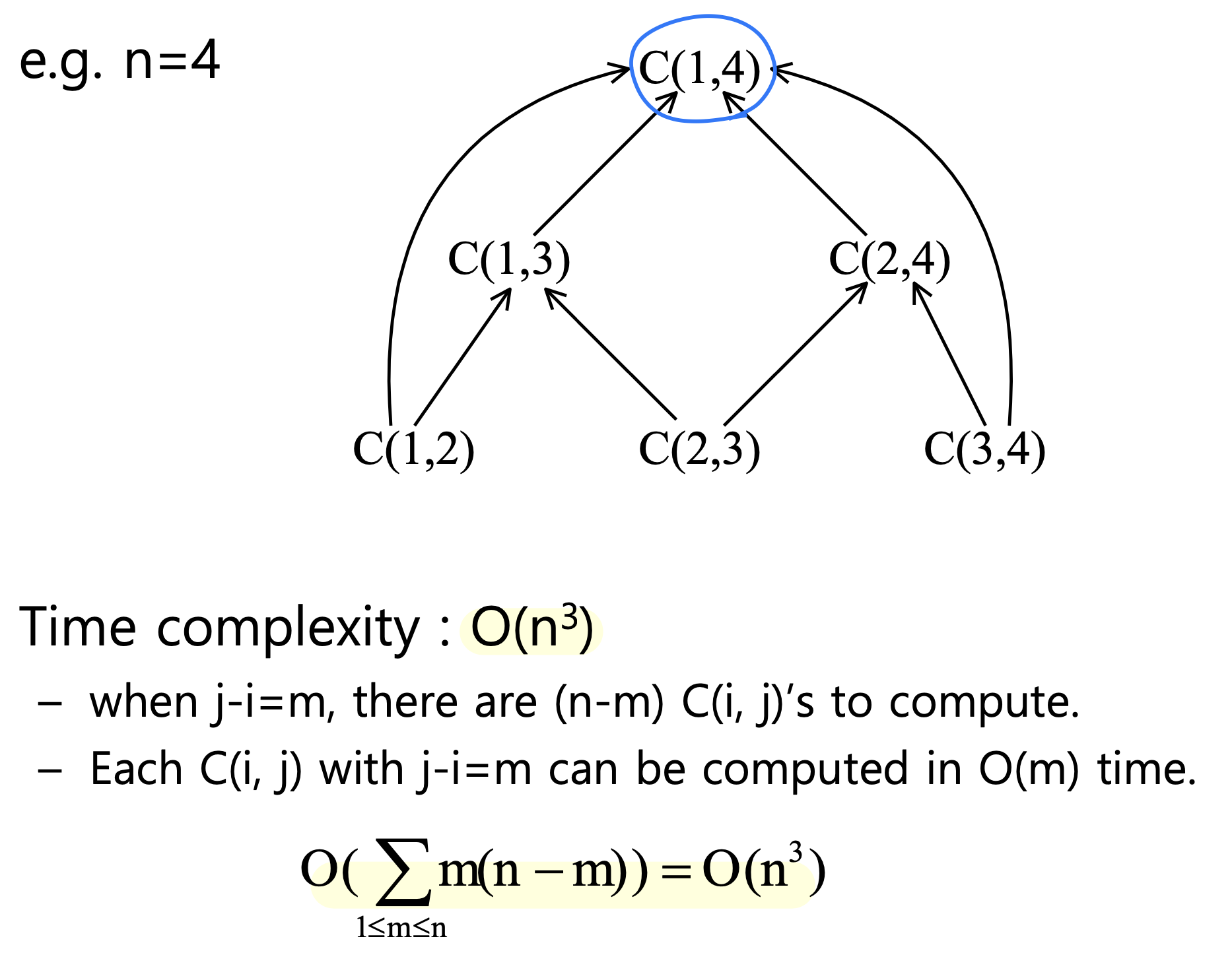
Computation relationships of subtrees
최단 경로 찾기 (Shortest Path)
- Dijkstar 알고리즘: Greddy Method 알고리즘
- 단일 출발점으로부터 각 정점까지의 최단 거리 및 경로 계산
- 모든 간선의 길이가 자연수임을 가정
- 음수 가중치 그래프에서 최단 경로를 찾는 방법
- 단 입력 그래프에 싸이클 상의 간선들의 가중치 합이 0보다 작은 음수 싸이클이 없어야함
- Bellman Ford 알고리즘:Dynamic Programming
- 음수 가중치 그래프에서 단일 출발점으로부터 각 정점까지의 최단 거리 및 경로를 계산
- 인접 행렬에서 O(n^3), 인접 리스트에선 O(mn) (n: 정점 개수, m: 간선 수)
- Floyd-Warshall 알고리즘: Dynamic Pogramming
- 음수 가중치 그래프에서 모든 정점 쌍 사이의 최단 경로 계산
- O(n^3)
Knapsack Problem
- 일부 항목의 경우 최대 총 값을 얻으려면 배낭을 채웁니다.
- 각각의 아이템은 어느 정도 무게와 어느 정도 가치를 가지고 있습니다.
- 우리가 운반할 수 있는 총 중량은 일정한 숫자 W에 지나지 않습니다. 따라서 우리는 품목의 무게와 가치를 고려해야 합니다.
(1) “0-1 knapsack problem”
(2) “Fractional knapsack problem”
(1)
항목은 분리할 수 없습니다.
항목을 가져가거나 말거나.
동적 프로그래밍으로 해결
쪼낄 수 없을 때
(2) 항목은 나눌 수 있습니다.
항목의 어떤 부분도 가져갈 수 있습니다.
탐욕스러운 알고리즘으로 해결했습니다.
- 최대 용량 W의 배낭과 n개의 항목으로 구성된 세트 S가 주어집니다
- 각 항목 i에는 가중치 wi 및 유익성 값 bi(모든 wi, bi 및 W는 정수 값)가 있습니다
- 문제: 포장 품목의 총 가치를 극대화하기 위해 배낭을 포장하는 방법은 무엇입니까?
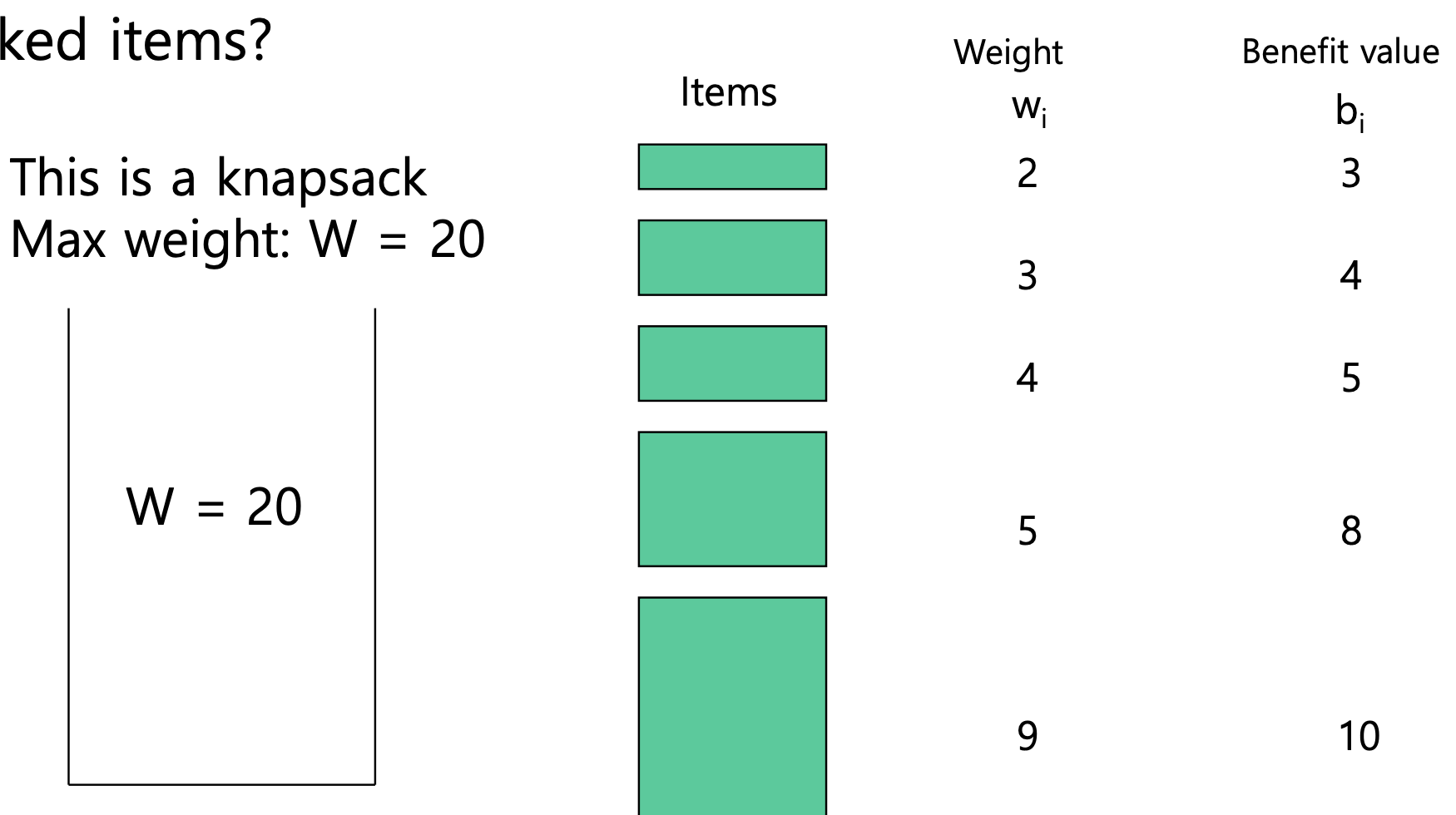
- 이 문제를 "0-1" 문제라고 합니다. 각 항목은 완전히 승인되거나 거부되어야 하기 때문입니다.
- 이 문제의 또 다른 버전은 "부분 배낭 문제"인데, 여기서 우리는 항목의 일부를 취할 수 있습니다.
Brute Force approach
- 가장 간단한 알고리즘
- n개의 항목이 있기 때문에 2n개의 항목 조합이 가능함
- 우리는 모든 조합을 조사하고 가장 많은 합계를 가진 것을 찾음
- 값 및 총 중량이 W 이하인 경우: 실행 시간은 O(2n)
- subproblems을 찾아야 함
항목에 1...n 레이블이 지정된 경우 하위 문제는 다음과 같습니다
Sk = {1, 2, ...k}에 대한 최적 솔루션 찾기
- 항목에 1...n 레이블이 지정된 경우 하위 문제는 Sk = {1, 2, ...k}에 대한 최적의 솔루션을 찾는 것임
- 유효한 하위 문제 정의지만 문제는 최종 솔루션(Sn)을 하위 문제(Sk)의 관점에서 설명할 수 있느냐는 것임 -> 불가능!
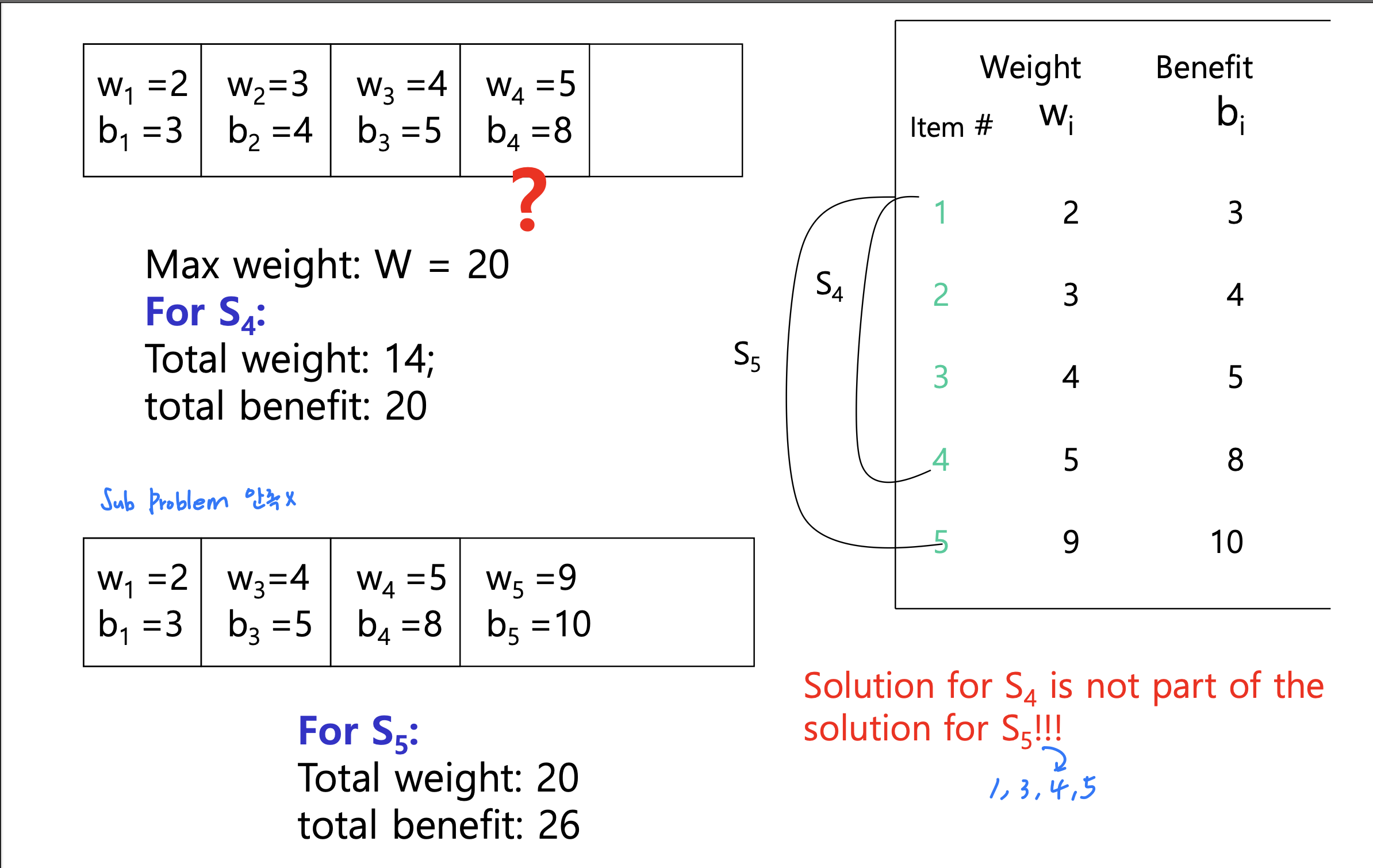
- S4용 솔루션은 S5용 솔루션의 일부가 아님
- 따라서 하위 문제에 대한 우리의 정의는 결함이 있으며 다른 문제가 필요함!
- 다른 매개 변수 w를 추가함
- w는 각 항목의 하위 집합에 대한 정확한 가중치를 나타냄 - 그러면 하위 문제는 B[k,w]를 계산하는 것임
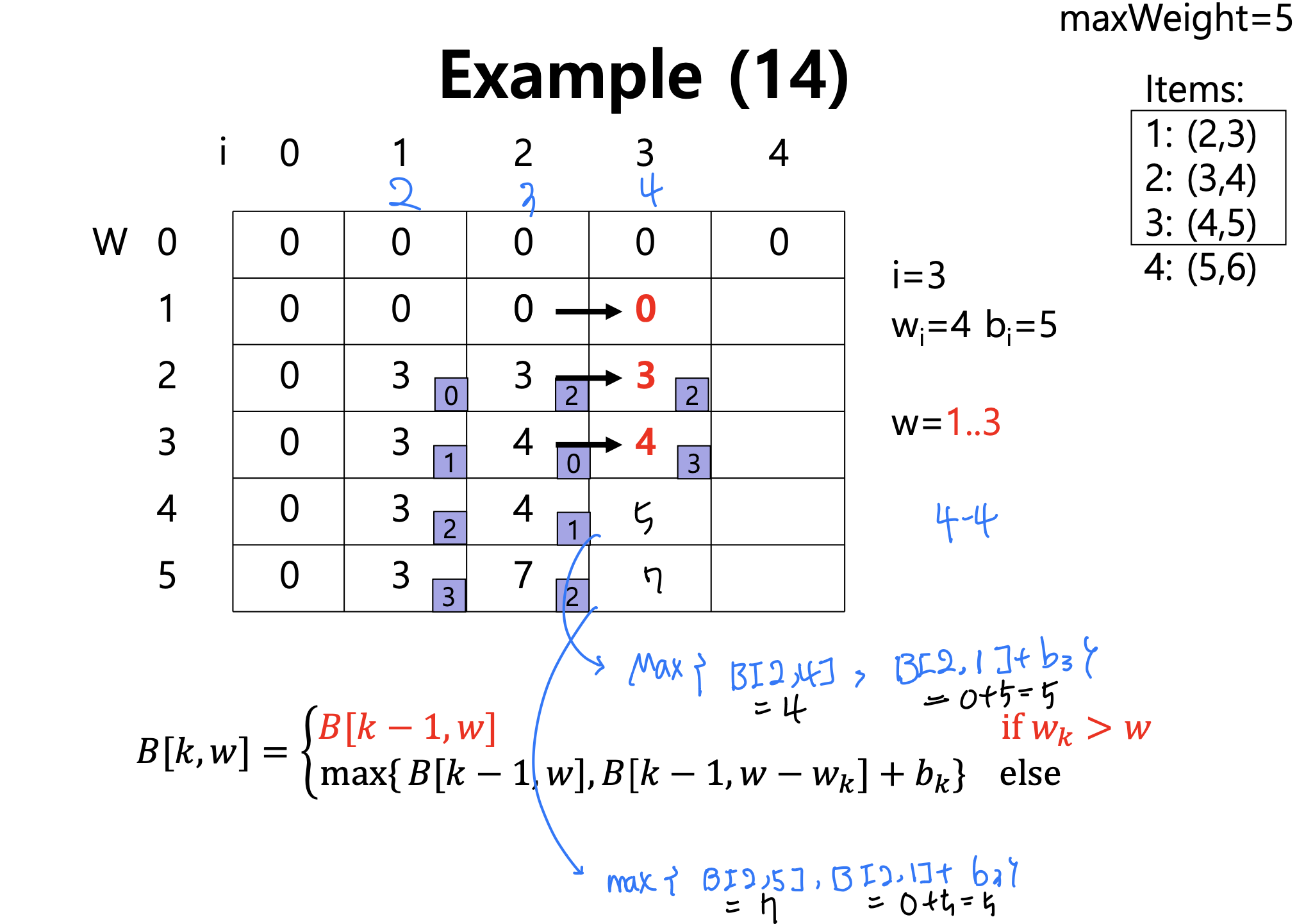
하위 문제에 대한 재귀 공식
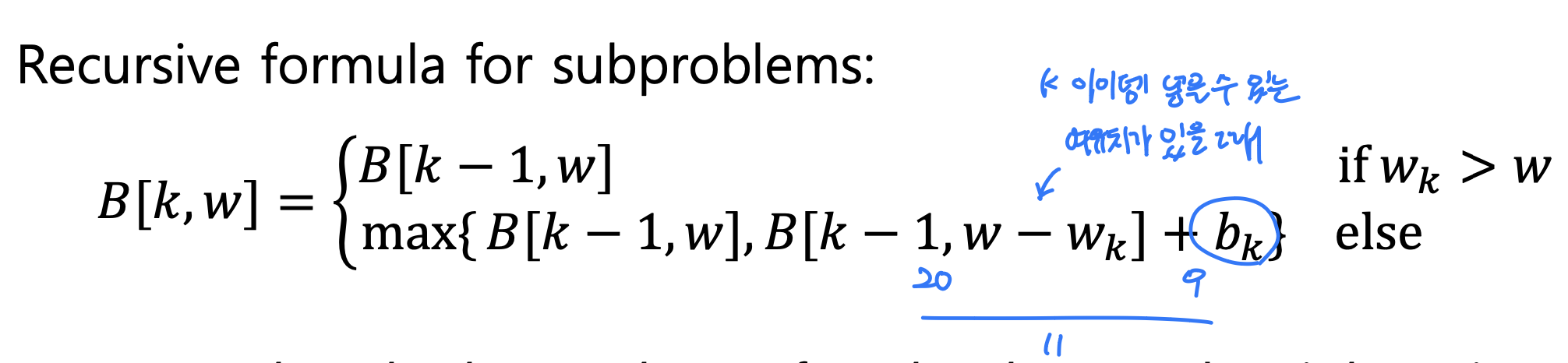
- t는 총 무게 w를 갖는 Sk의 최고 부분 집합이 다음 중 하나라는 것을 의미합니다
1) 총 중량 w를 갖는 Sk-1의 최고 부분 집합, 또는
2) 총 중량 w-wk + 항목 k를 갖는 Sk-1의 최고 하위 집합 - 총 가중치가 w인 Sk의 가장 좋은 부분 집합(항목 k 포함 여부)
- 첫 번째 경우: wk > w. 항목 k는 솔루션의 일부가 될 수 없음
만약 그렇다면 총 중량은 > w가 될 것이기 때문에 허용되지 않음 - 두 번째 경우: wk <= w. 그러면 항목 k가 솔루션에 포함될 수 있으며, 우리는 더 큰 가치를 가진 케이스를 선택함
- 첫 번째 경우: wk > w. 항목 k는 솔루션의 일부가 될 수 없음
예제
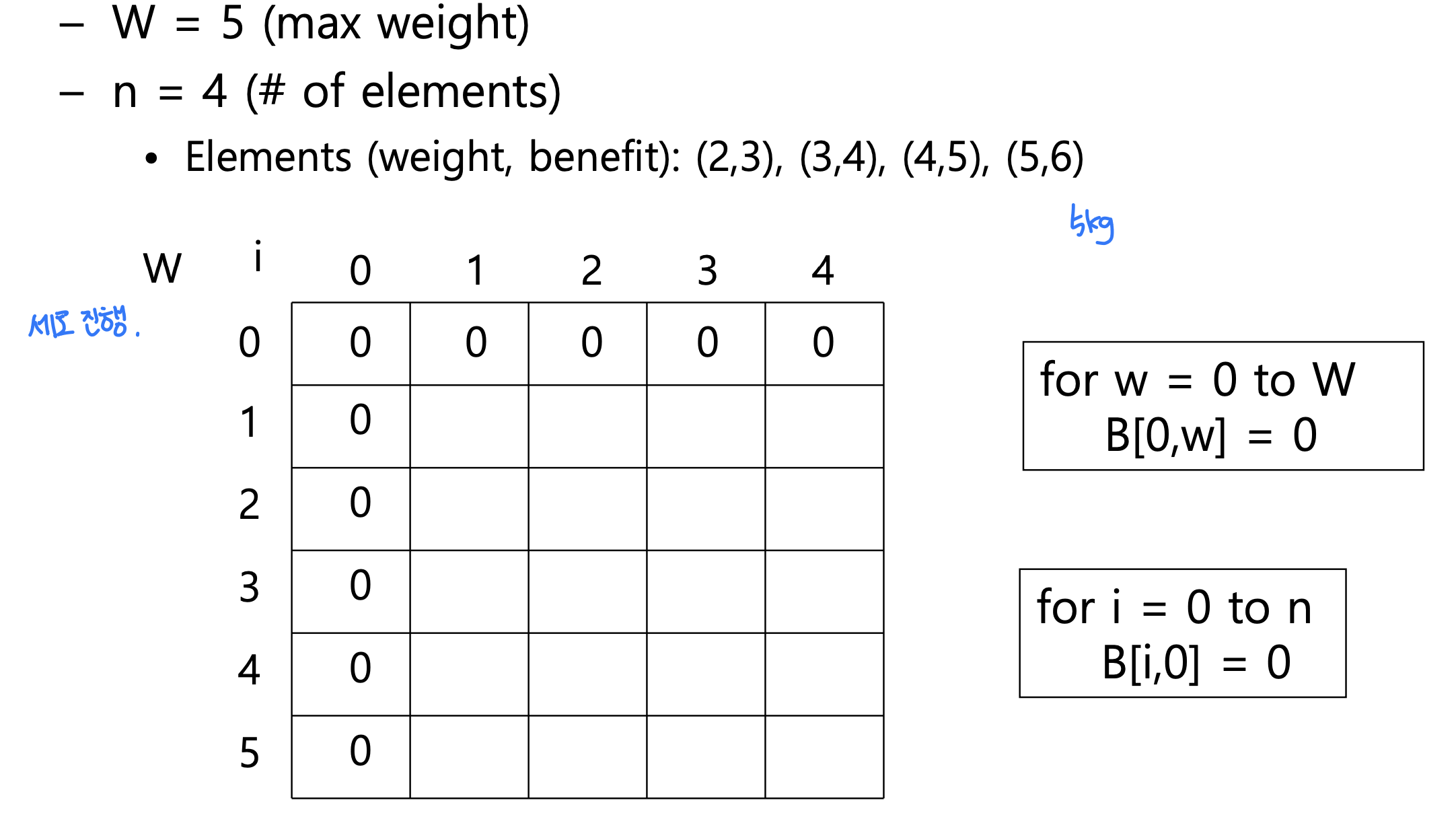
정리
- Top-down (recursive) 방법이 아니라 문제를 가장 작은 크기부터 시작해서 키워 나가는 방법
- Overlap 해결
- 알고리즘 수행 시간: O(n * W)


