개요
- 동적 프로그래밍과 유사
- 최적화 문제에 적용됨
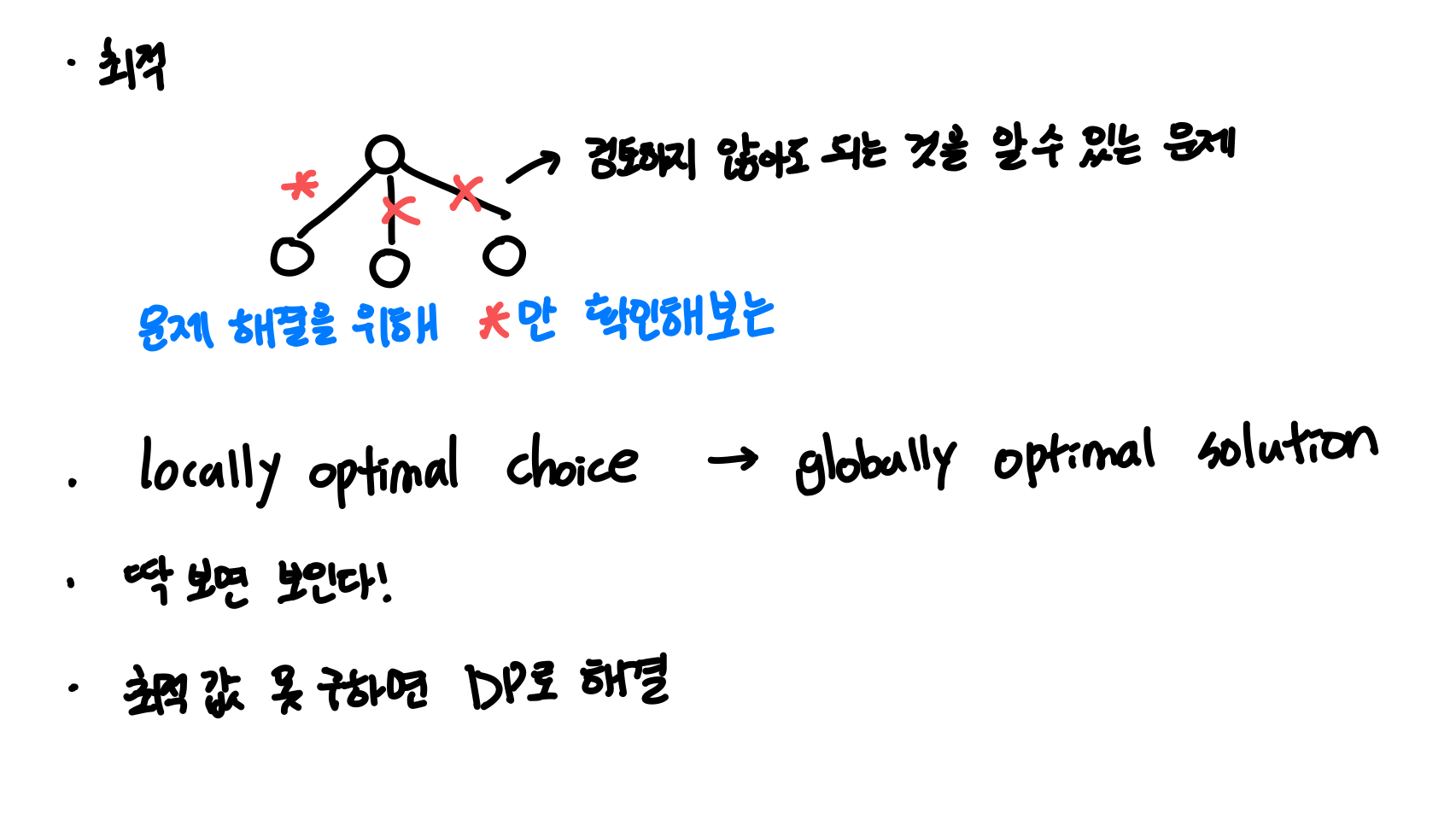
- 우리가 선택해야 할 것이 있을 때, 지금 당장 가장 잘 보이는 것을 만들어라
- 전체적으로 최적화된 솔루션을 얻기 위해 지역적으로 최적의 선택을 하라
- 하위 문제가 해결되기 전에 선택함
- 탐욕스러운 알고리즘이 항상 최적의 솔루션을 제공하는 것은 아니지만, 때로는 그렇게 하기도 함
- 많은 문제에서 동적 프로그래밍 접근 방식보다 훨씬 더 신속하게 최적의 솔루션을 제공함
그래프에서 그리디 적용하기
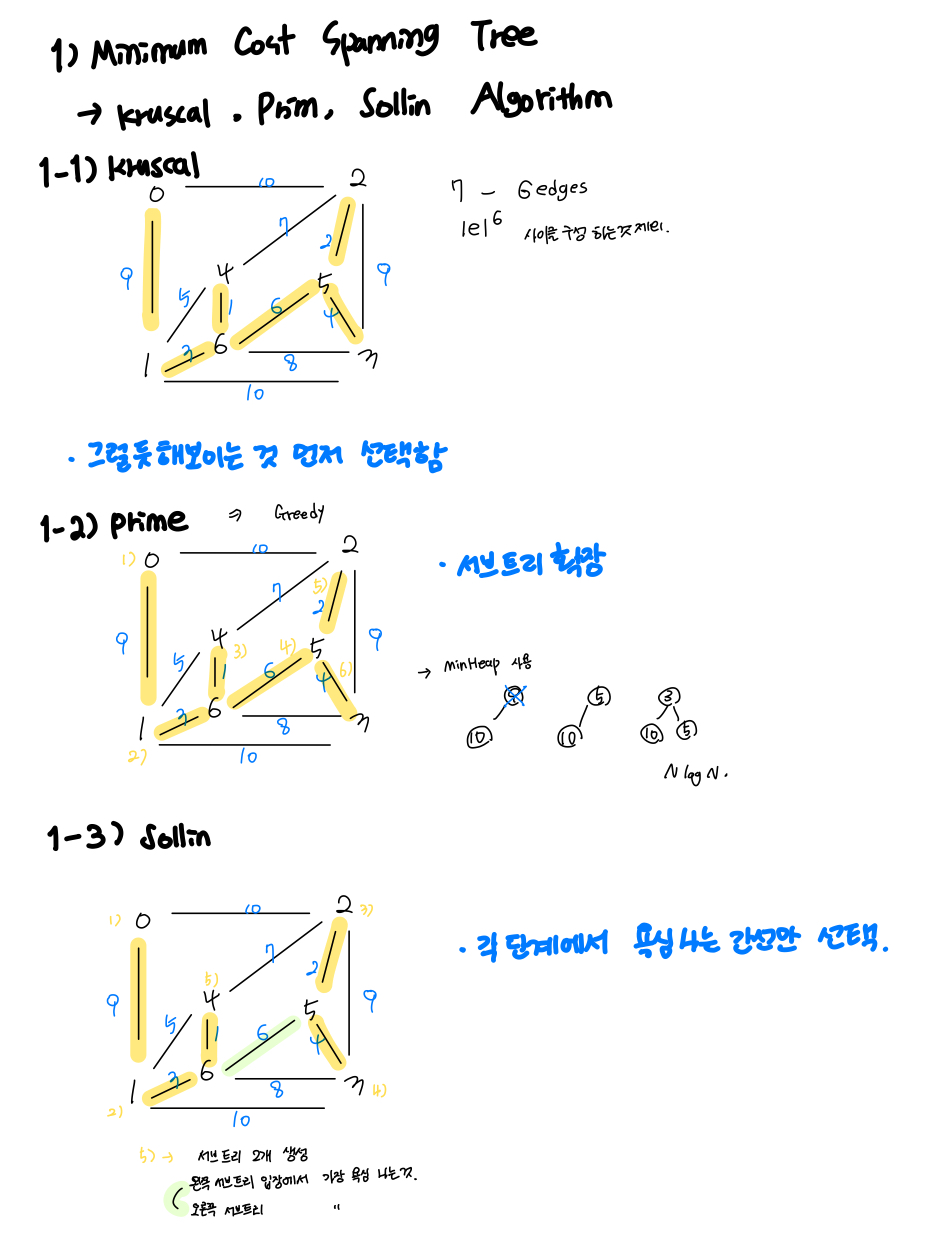
- Minimum Cost Spanning Tree
- Kruskal’s Algorithm
- Prim’s Algorithm
- Sollin’s Algorithm
- Shortest Path
- Dijkstra Algorithm
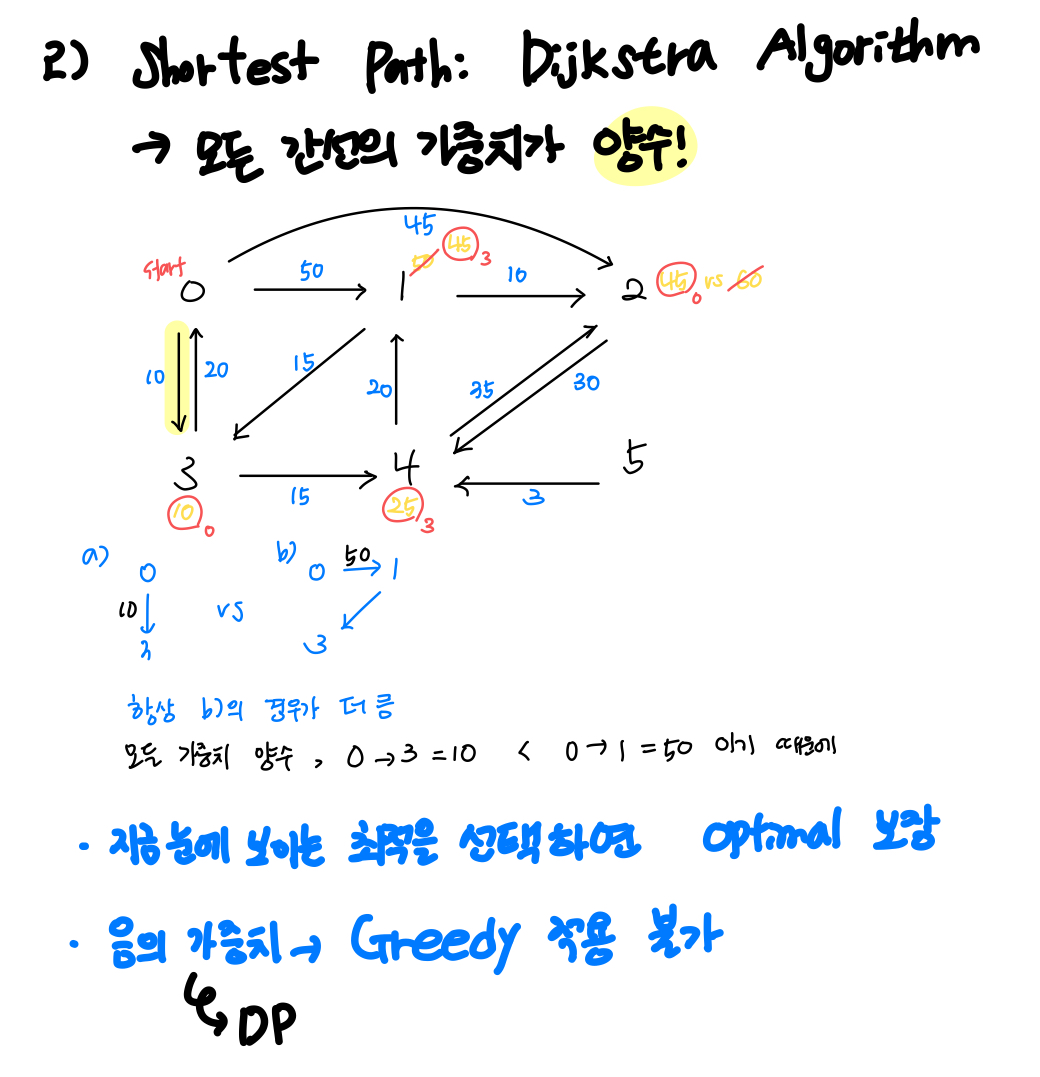
- Dijkstra Algorithm
활동 선택 문제
- 공통 자원을 독점적으로 사용해야 하는 여러 경쟁 활동을 예약하는 문제임
- n개의 활동에는 공통 리소스의 독점적인 사용이 필요함. 예를 들어 강의실 사용을 예약함
- 일련의 활동 S={a1, ..., an}.
- ai는 반쯤 열린 간격인 [si, fi] 기간 동안 자원이 필요함
- si = 시작 시간 및 fi = 완료 시간
- 참고: 다른 여러 가지 목표가 있을 수 있음
- 강의실을 가장 오래 예약합니다.
- 소득 임대료를 최대화합니다.
- n개의 수업과 1개의 강의실이 주어지면 최대 수업 수를 선택합니다.
목표: 중복되지 않는(상호 호환 가능한) 활동의 가장 큰 집합을 선택합니다.
예제

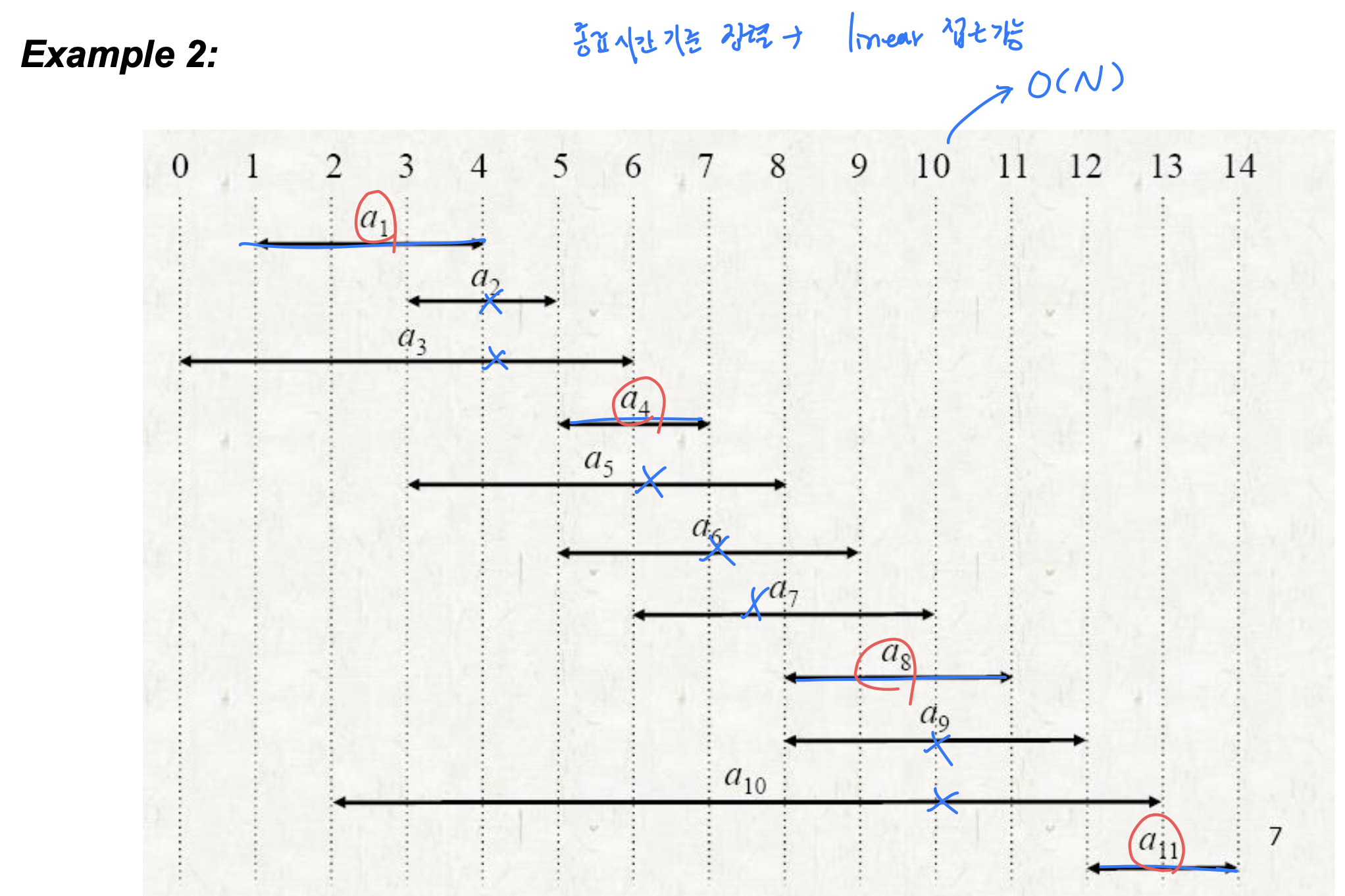
- 정답: 4
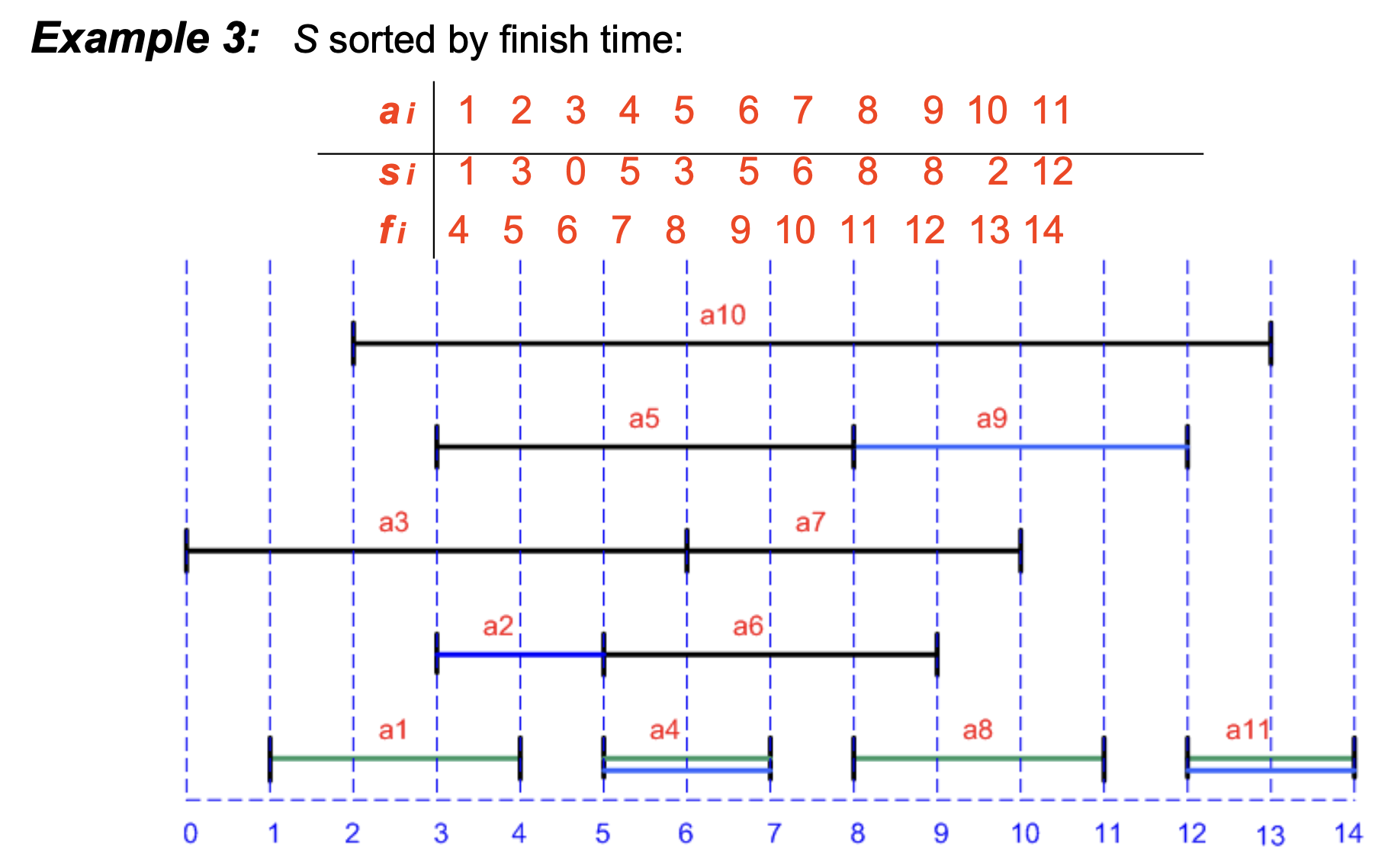
- 상호 호환되는 최대 크기 집합: {a1, a4, a8, a11}.
- not unique -> {a2, a4, a9, a11}.
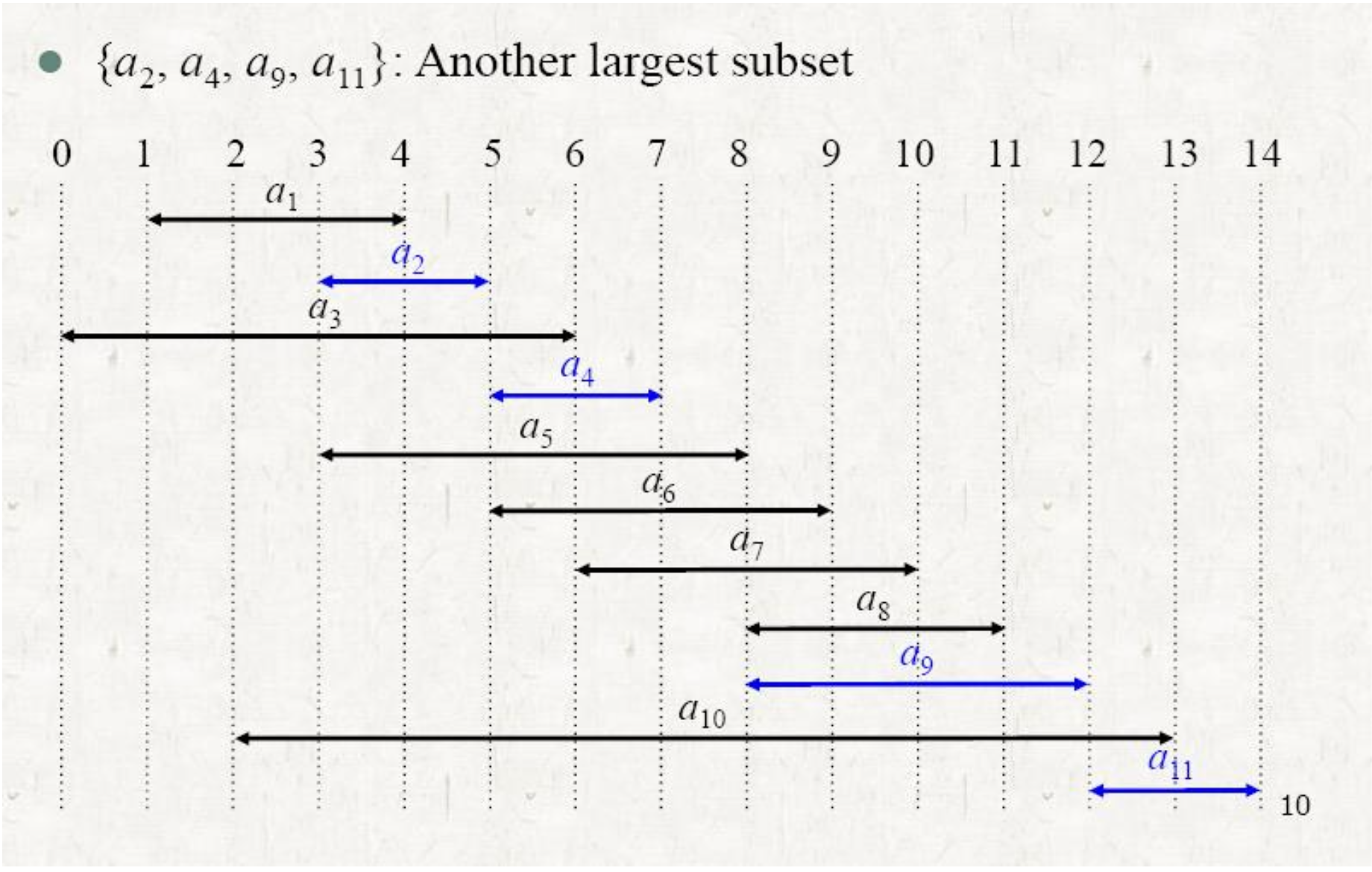
최적의 서브 구조

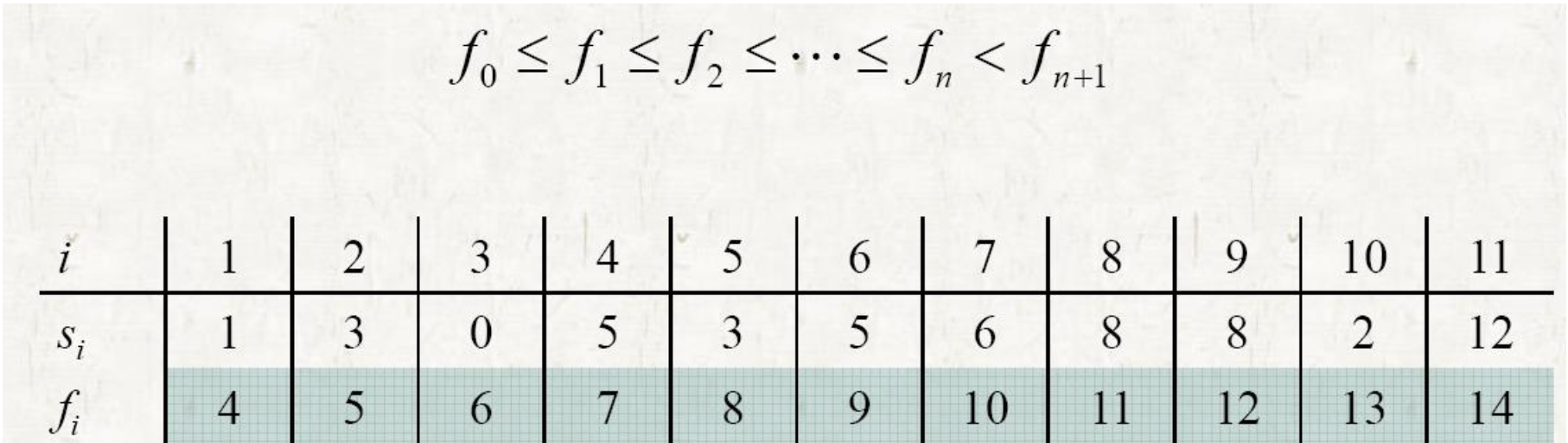

- 비어 있지 않은 모든 Sij를 고려하고, 가장 빠른 완료 시간(fm = min {fk : ak ∈Sij})을 Sij에서 활동으로 지정
- 활동 팀은 일부 Aij에 있습니다.
- 하위 문제 Sim이 비어 있으므로 am을 선택하면 다음과 같음
- Smj는 비어 있지 않을 수 있는 유일한 하위 문제입니다.
- 활동 am은 어떤 Aij에 있음
– – – - ak: Aij에서의 첫 번째 마무리 활동
- ak = am이면 완료.
- ak ≠ am인 경우, am을 추가하고 ak를 Aij로부터 제거함
- fm ≤ fk 및 Aij의 다른 모든 활동은 ak 종료 후에 시작되기 때문에 결과로 나타난 Aij는 또 다른 최적의 솔루션입니다.

- fm ≤ fk 및 Aij의 다른 모든 활동은 ak 종료 후에 시작되기 때문에 결과로 나타난 Aij는 또 다른 최적의 솔루션입니다.
가장 이른 마무리 작업을 하나씩 선택합니다.

Greedy VS DP
- 탐욕 선택 속성
- 하위 문제가 하나만 생성됩니다.
- 하위 문제가 해결되기 전에 선택합니다.
-> Top-down: 증명된 최적의 값을 선택해 나머지를 cutting 해나가는 방식
- 동적 프로그래밍
- 하위 문제가 해결된 후 선택합니다.
- 몇 가지 하위 문제가 발생할 수 있습니다.
-> Bottom-up: 계산한 값 재사용
현재 가장 좋을 것 같은 선택은 가져감.
• 활동 선택 과정
1. 최적의 하위 구조를 결정합니다.
2. 재귀적 해결책을 개발합니다.
3. 재귀의 어느 단계에서든 최적의 선택 중 하나가 탐욕스러운 선택이라는 것을 증명합니다. 그러므로, 탐욕스러운 선택을 하는 것은 항상 안전합니다.
4. 탐욕스러운 선택으로 인해 발생하는 하위 문제 중 하나를 제외한 모든 것이 비어 있음을 보여줍니다.
5. 재귀적 탐욕 알고리즘을 개발합니다.
6. 반복 알고리즘으로 변환합니다.
- 처음에는 동적 프로그래밍처럼 보였습니다.
- 일반적으로 이러한 단계를 간소화합니다.
- 다음을 염두에 두고 하부 구조를 개발합니다
- 탐욕스러운 선택을 하는 것,
- 단 하나의 하위 문제를 남깁니다.
활동 선택을 위해, 우리는 탐욕스러운 선택이 Sij에서 오직 i만 변화하고 j는 n + 1로 고정되었음을 암시한다는 것을 보여주었습니다.
- 이를 통해 탐욕스러운 알고리즘을 염두에 두고 시작할 수 있었습니다:
– Si = {ak ∈ S : fi ≤ sk }을(를) 정의합니다.
– 그런 다음 Si에서 끝내기 위한 탐욕스러운 선택이 Si에 대한 최적의 솔루션 Sm에 대한 최적의 솔루션과 결합되었음을 보여줍니다.
Sm에 대한 최적 솔루션 -> Si에 대한 최적 솔루션.
• 일반적인 간소화 단계:
1. 최적화 문제를 우리가 선택하는 문제로 제시함
해결해야 할 하위 문제가 하나 남아 있음
2. 탐욕스러운 선택을 하는 최적의 해결책이 항상 있다는 것을 증명하고,
그래서 탐욕스러운 선택은 항상 안전함
3. 하위 문제에 대한 탐욕스러운 선택과 최적의 해결책을 보여줌
- 그 문제에 대한 최적의 해결책.
• 그리디 알고리즘이 최적인지 알 수 있는 일반적인 방법은 없습니다,
하지만 두 가지 핵심 요소는- 탐욕스러운 선택 속성과
- 최적의 하부 구조
지역적으로 최적의(욕심이 많은) 선택을 함으로써 전체적인 최적의 솔루션을 얻을 수 있음
- 동적 프로그래밍:
- 각 단계에서 선택합니다.
- 선택은 하위 문제에 대한 최적의 솔루션을 아는 것에 달려 있습니다.
- 하위 문제를 먼저 해결합니다.
- 상향식 문제를 해결합니다.
- Greedy:
- 각 단계에서 선택합니다.
- 하위 문제를 해결하기 전에 선택하십시오.
- 하향식으로 해결합니다.
- 일반적으로 활동 선택을 위해 수행한 작업을 통해 탐욕스러운 선택 속성을 보여줍니다:
– 전체적으로 최적화된 솔루션을 살펴봐라
– 욕심 많은 선택이 포함되면 끝

– 그렇지 않으면, greedy 선택을 포함하도록 수정하고, 다음과 같은 다른 해결책을 제시함 - greedy 선택 속성을 통해 효율성을 높일 수 있습니다.
- 입력을 사전 처리하여 탐욕스러운 순서로 정렬합니다.
