중간-일치 공격
- 공격자는 M값에 대해 정렬된 2개의 테이블을 만들어냄
- 그러나, 아래의 그림과 같이 양쪽 테이블에서 M의 값이 같은 k1과 k2의 쌍을 찾을 때까지 M에 대한 값을 비교해봄
- 두 개의 키의 조합에 대해 전수 조사를 하는 것이기 때문에 최소 한 쌍이 있어야 함
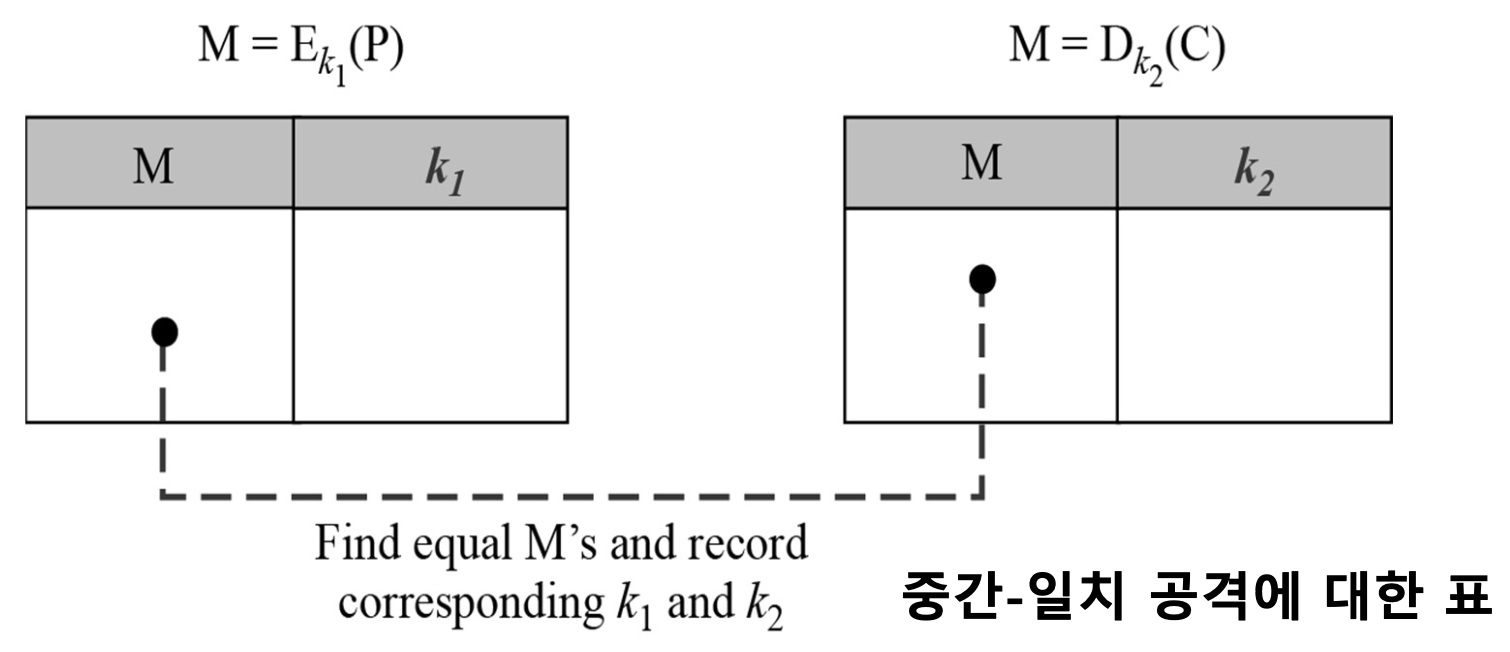
Ek1(P) = Dk2(C)
- 오직 한 쌍의 k1과 k2만 있다면 공격자는 2개의 키(k1, k2)를 찾게 되는 것임 이때, 하나 이상의 후보가 있다면 공격자는 다음 단계로 이동함
- 가로챈 또 다른 평문-암호문 쌍을 갖고 후보 키 쌍을 검사해봄 만일 하나 이상의 후보 키 쌍이 있다면, 최종적으로 유일한 쌍을 찾을 때까지 단계2를 반복함
- 실제로 약간의 평문-암호문 쌍을 위의 두 번째 단계에 적용하면 키를 찾을 수 있음이 증명됨
- 이것은 공격자가 2^112개의 키-검색 조사를 하는 것 대신 2^56개의 키-검색 검사를 2번 실시하면 됨을 의미함
- 이때 첫 번째 단계에서 하나 이상의 후보 키들이 발견되면 약간의 검사 횟수가 더 필요하게 됨
- 이는 하나의 DES에서 이중 DES로 이동하면서 키의 가능한 경우의 수가 실제로 2^56에서 2^112가지가 아닌, 2^57가지로 안전도가 약간 향상됨을 의미함
2개의 키를 갖는 삼중 DES
- 두 개의 키 k1과 k2만을 사용함
- 첫 번째와 세 번째 단계에서는 k1을 사용
- 두 번째 단계에서는 k2를 사용
- 하나의 DES를 갖고 삼중 DES를 만들기 위해
- 암호화 과정의 중간 단계에서는 DES의 복호 알고리즘 사용
- 복호화 과정의 중간 단계에서는 DES의 암호 알고리즘 사용
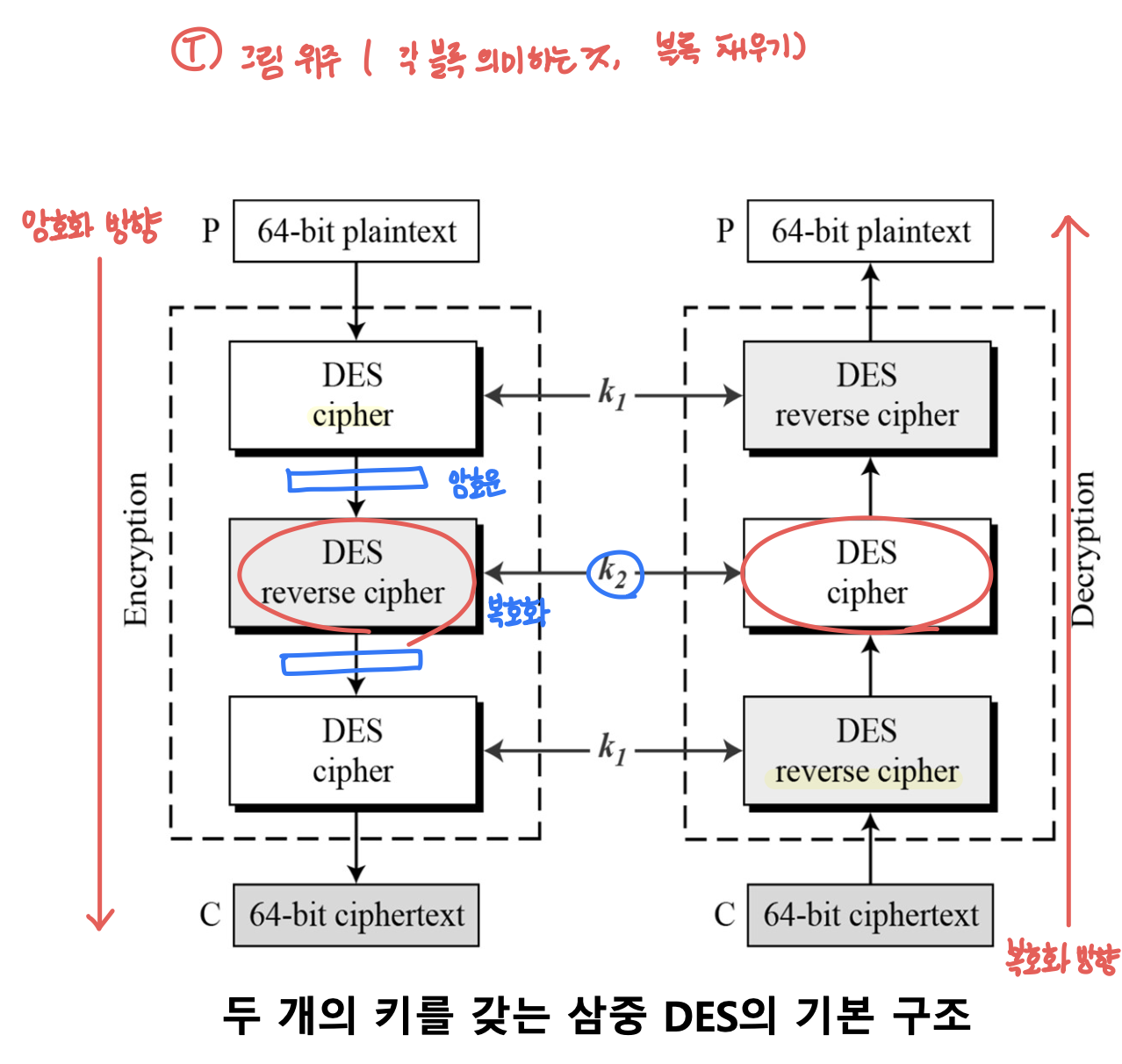
- 이때 k1 = k2 = k라면, 키 k를 갖는 하나의 DES를 가지고 암호화 된 메시지는 삼중 DES를 가지고 복호화할 수 있음
- 두 개의 키를 가진 삼중 DES는 기지 평문 공격에 취약하더라도 이중 DES보다는 훨씬 강력한 것으로 알려져 있음
평문-암호문-키 등식 관계 성립되면 안됨!
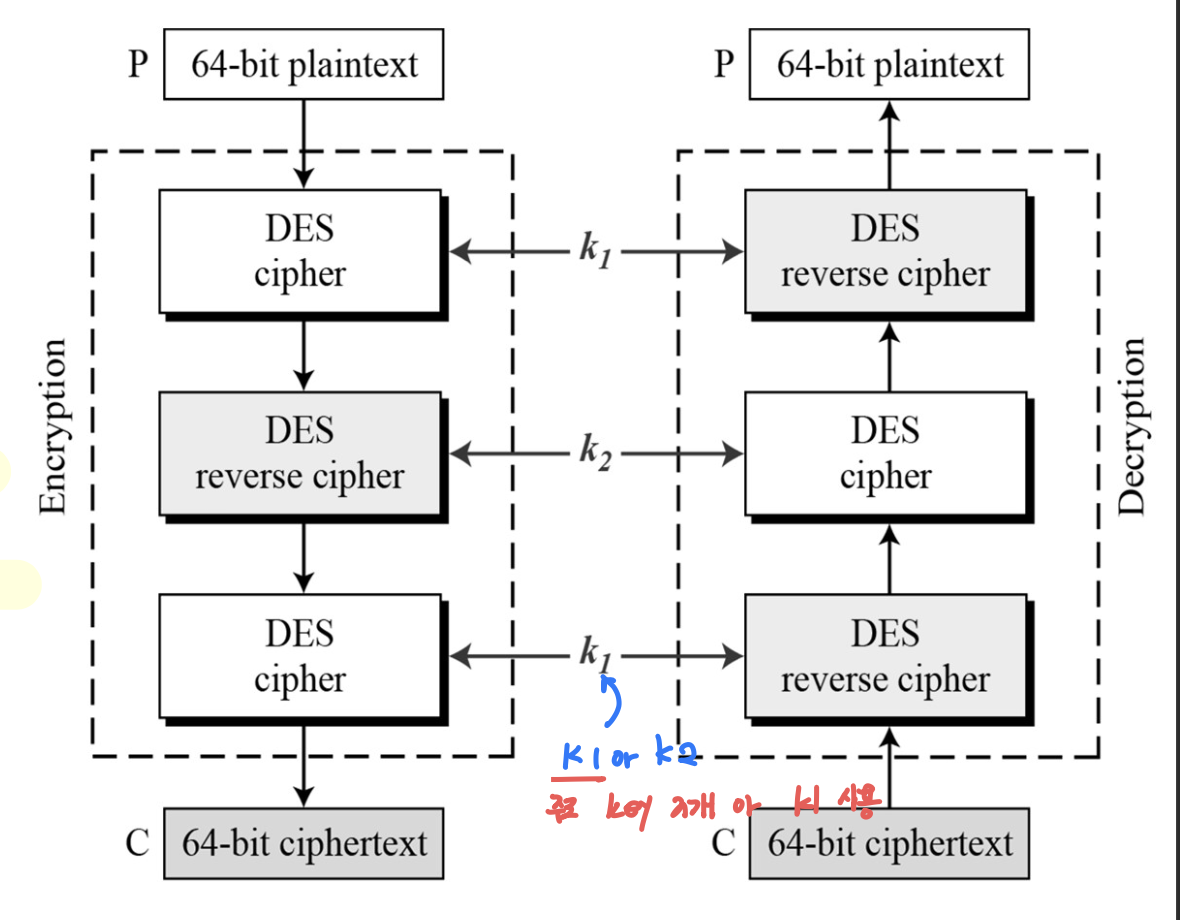
3개의 키를 갖는 삼중 DES
- 암호화 과정에서 3번의 DES 암호 알고리즘을 사용하고, 복호화 과정에서 3번의 복호 알고리즘 사용하는 원리로 설계 가능
- 그러나 DES를 한 번만 사용하는 방법과의 호환성을 고려해 위의 원칙과는 다른 설계 방식으로 구현함
- 암호화 과정: 암호화 -> 복호화 -> 암호화
- 복고화 과정: 복호화 -> 암호화 -> 복호화
- 각 단계에서 사용되는 키 값은
- k1 = k
- k2 = k3 = c (c: 수신자가 임의로 선택한 값)
비대칭 키 암호 시스템
소수와 나머지 정리
소수
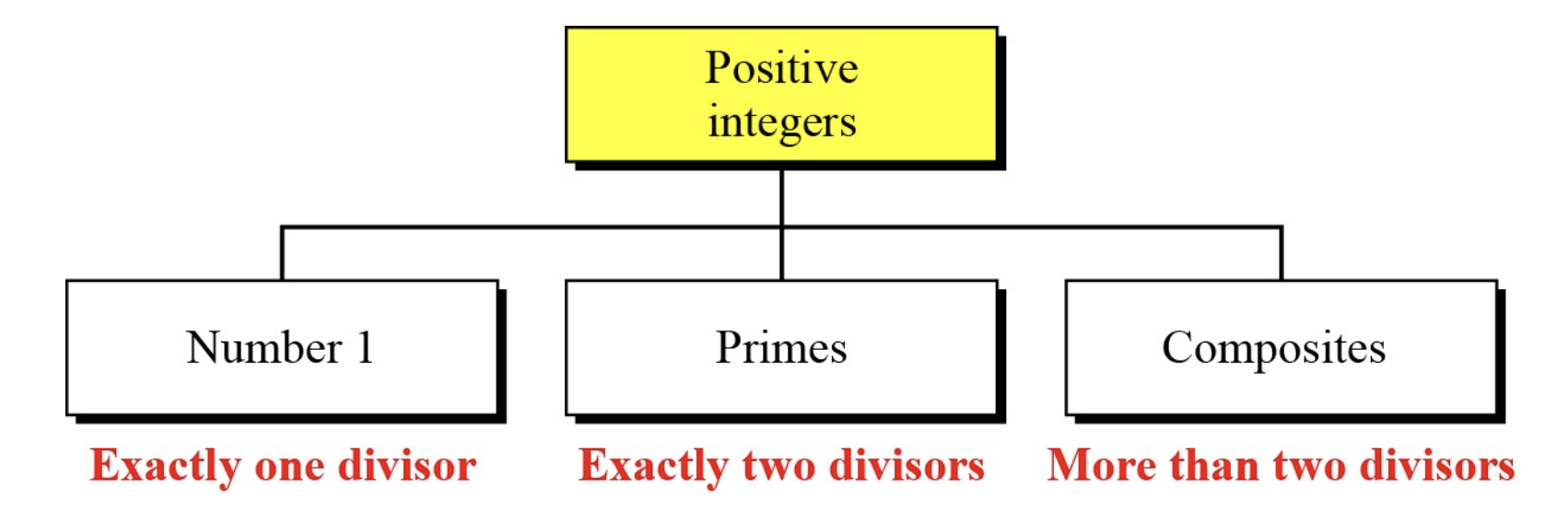
양의 정수의 3가지 종류: 1. 소수, 합성수
- 자기 자신만을 약수로 갖는 수 -> 1
- 1과 자기 자신만을 약수로 갖는 수 -> 소수 (Primes)
- 3개 이상의 약수를 갖는 수 -> 합성수(Composites)
서로소
- 두 정수 a와 b에 대해 1이외의 공약수가 존재하지 않는 경우
- 즉, a의 양의 약수의 집합을 A, b이 양의 약수의 집합을 B라 할 때, A ∩ B = {1}
- 서로소와 동치인 명제
- a와 b의 최대공약수가 1임
- a와 b의 최소공배수가 ab임
- a와 b는 서로소임
- 표기법: a ⊥ b
소인수분해
- 1보다 큰 사연수를 소인수(=소수인 인수)들만의 곱으로 나타내는 것
- 산술의 기본 정리
- 모든 양의 정수는 소수들의 곱으로 표현될 수 있으며, 그 방법은 유일하게 존재함
- 그러나 양의 정수를 소인수분해 하는 방법 자체는 언급 x -> 존재 자체만 증명
- 실제로 소인수 분해를 다항시간 내에 수행하는 알고리즘은 아직까지 발견되지 않음
- 특히 큰 수에 대한 소인수분해는 매우 어려운 문제임
- 따라서, 소인수분해는 현대 암호학에서 핵심 기술로서 중요하게 사용되고 있음
🇨🇳 중국인의 나머지 정리
- 중국의 고전서 "손자산경"에 나오는 문제
3으로 나눴을 때 2가 남고, 5로 나눴을 때 3이 남고, 7로 나눴을 때 2가 남는 수는?
- 답 == 합동 방적식의 해
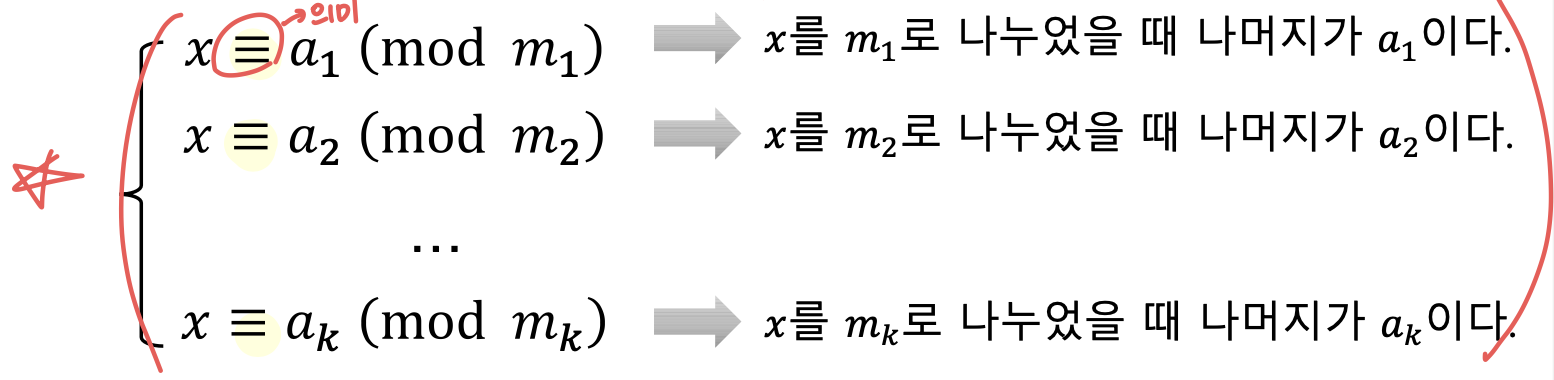
- 합동 방정식의 유일한 해의 존재성에 기반해 해를 구하는 방법
모듈러 합동 ≡
- x = a mod b
- a를 b로 나누었을 때, 나머지가 x이다.
- x ≡ a (mod b)
- 모듈러 합동
- x를 b로 나누었을 때, 나머지가 a임
비대칭 키 암호 시스템
- 비대칭 키 암호 시스템에서는 두 개의 서로 다른 키를 사용
- 공개키: 누구에게나 공개가 가능한 키
- 비밀키: 자신만이 갖고 있는 키 (= 개인키 or 비공개키)
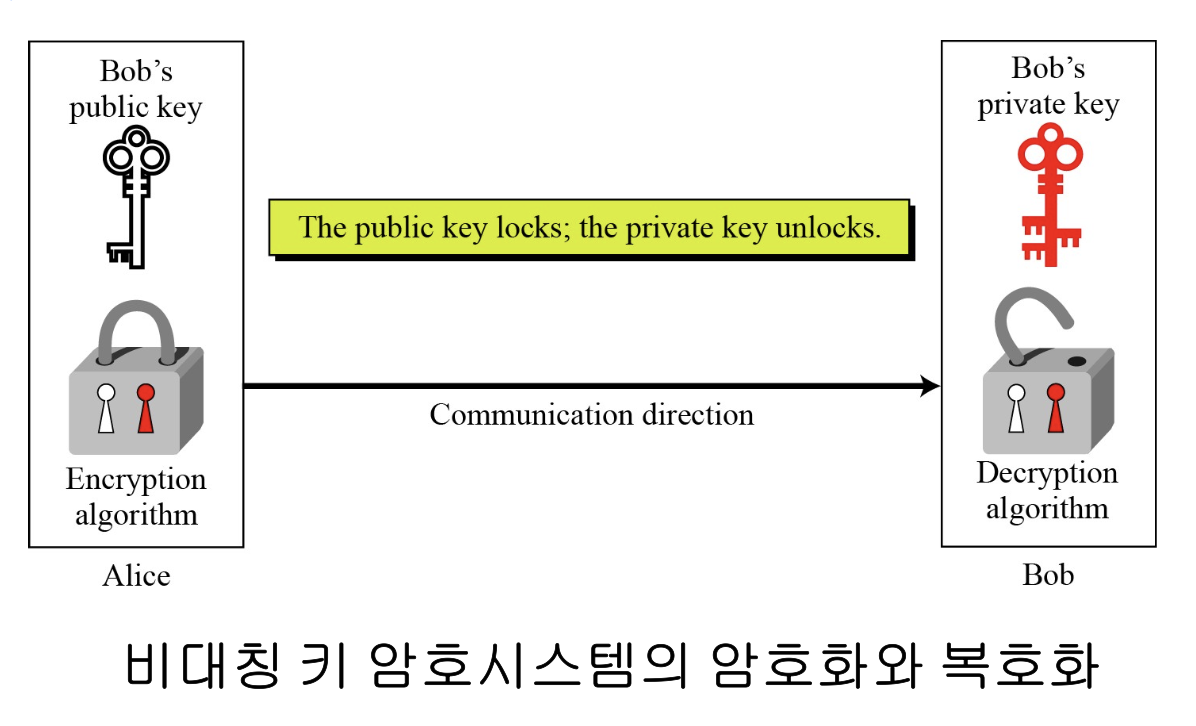
어떤 키로 암호화를 수행하는가?
case1. 공개키로 암호화하는 경우
- 송신자가 공개키로 평문을 암호화한 후 수신자에게 전송
- 수신자는 자신이 갖고 있는 개인키를 이용해 수신된 암호문을 복호화
- 예) 공개키 암호 알고리즘: RSA, Rabin ...
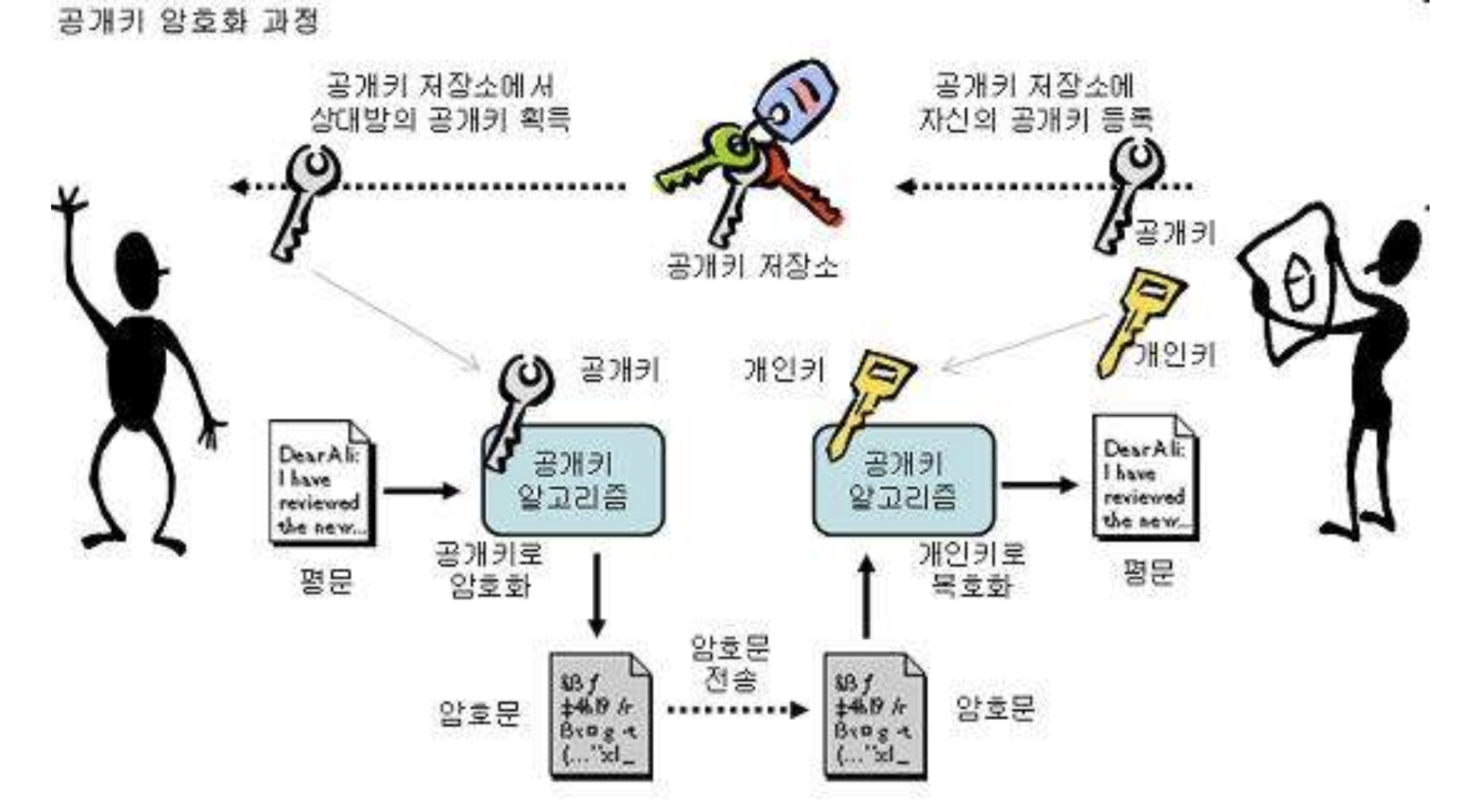
case2. 개인키로 암호화는 경우
- 송신자는 자신이 갖고 있는 개인키를 활용해 평문을 암호화하고 이를 수신자에게 공개키와 함께 전달
- 이때, 수신자는 공개키를 이용해 암호문을 평문으로 복호화
- 이 방법은 데이터의 보안보다는 데이터를 전송하는 송신자의 신원을 보장하는 데 더 큰 의미가 있음
암호문을 공개키로 복호화 -> 공개키와 쌍을 이루는 비밀키로 암호화되었음을 의미 -> 이 비밀키는 오직 송신자만 갖고 있는 것 -> 송신자의 신원이 확실하게 보장됨을 의미함
- 예) 전자 서명 (공인 인증서)
비대칭키 암호의 일반적인 아이디어
- 2진수 비트가 아닌 정수로 다룸 (소인수분해 응용을 위해)
- 대칭키 암호 시스템과 다르게, 비대칭키 암호 시스템에서는 평문이나 암호문이 정수로 다루어짐
- C = f(K_public, P)
- P = g(K_private, C)
일방향 함수
- 비대칭키 암호 시스템을 구성하는 핵심 아이디어 중 하나
- One-Way Function (OWF)
- 함수 f는 계산이 쉬운 반면에, 역함수 f^(-1)은 계산이 어려움
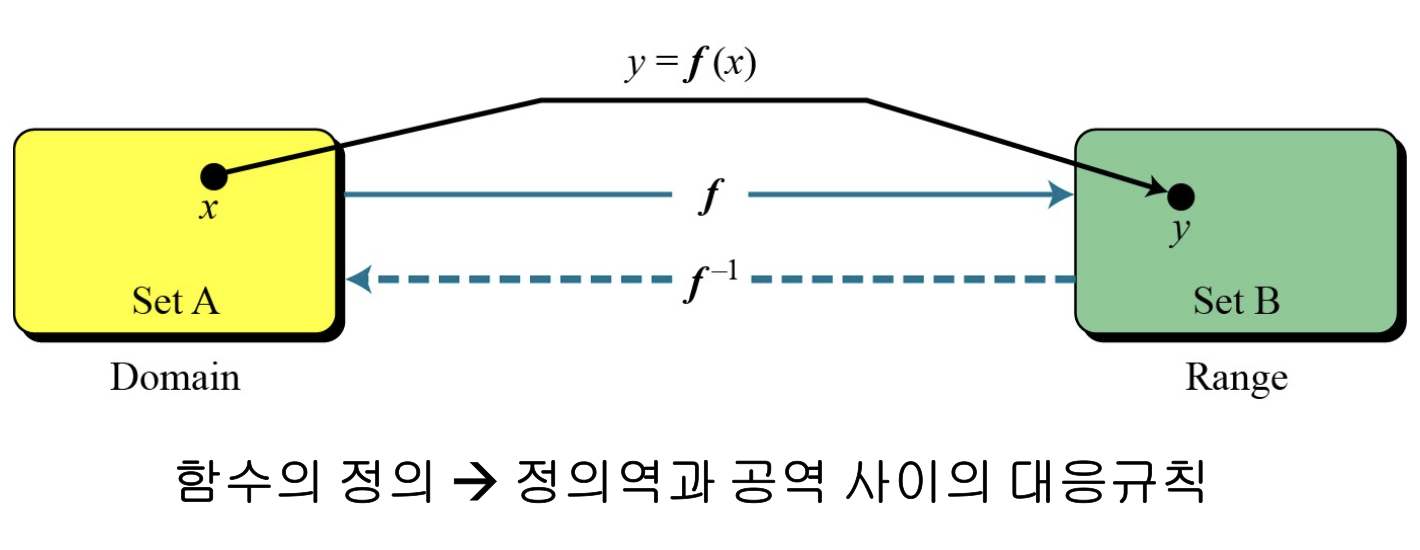
- 함수 f는 계산이 쉬운 반면에, 역함수 f^(-1)은 계산이 어려움
트랩도어 일방향 함수
- Trapdoor One-Way Function (TOWF)
- 보통 일방향 함수처럼 함수의 역을 구하는 것은 어렵지만, 트랩도어라고 부르는 특수한 비밀정보가 있으면 쉽게 역을 구할 수 있는 함수
- 어떤 비밀 값 t에 대해서, x에 대한 t가 없을 때는 f로부터 x를 구하기 어렵지만, t가 주어졌을 때 x값을 쉽게 찾을 수 있다면, 함수 f는 트랩도어 함수임
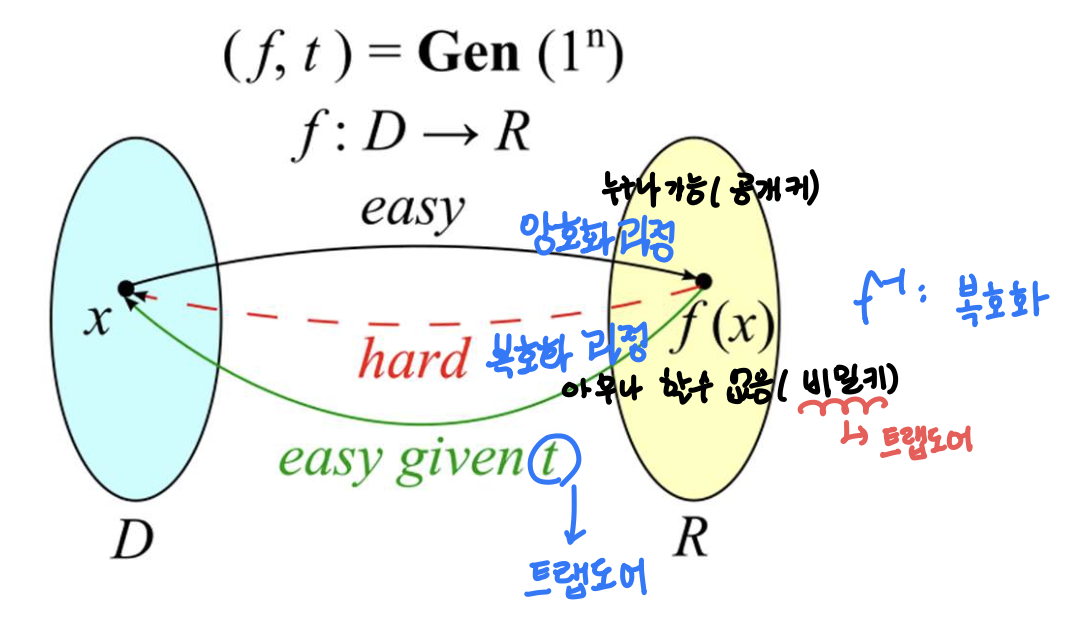
예제1
n이 매우 큰 수라고 가정하자. 이 경우, n = p x q는 일방향 함수이다. 이때, 주어진 p와 q로부터 n을 계산하는 것은 매우 쉽다. 하지만 주어진 n으로부터 p와 q를 계산하는 것은 매우 어렵다. -> 소인수분해 문제
예제2
n이 매우 큰 수라고 가정하자. 함수 y = xk mod n은 트랩도어 일방향 함수이다. 이 때 x, k, n으로부터 y를 계산하는 것은 쉽다.
- 하지만 상기 관계식에서 y, k, n이 주어졌을 때 x를 계산해내는 것은 매우 어려움 -> 이산 대수 문제 및 ElGamal 암호
- 한편 k x k' = 1 mod f(n)이 되는 트랩도어 k'를 알고 있다면, x = yk' mod n을 이용해 x를 구할 수 있음 -> RSA, Rabin 암호 (RSA 확장)
RSA 암호 시스템
개요
- RSA: 개발자 3명 이름 참조해서 작명
- 가장 많이 사용되는 공개키 알고리즘
- RSA는 모듈로 지수 계산을 이용해 암호화/복호화를 함
- 이것을 공격하려면 공격자는
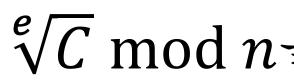를 계산해야 함 -> 지수 복잠도 (공격이 매우 어려움)
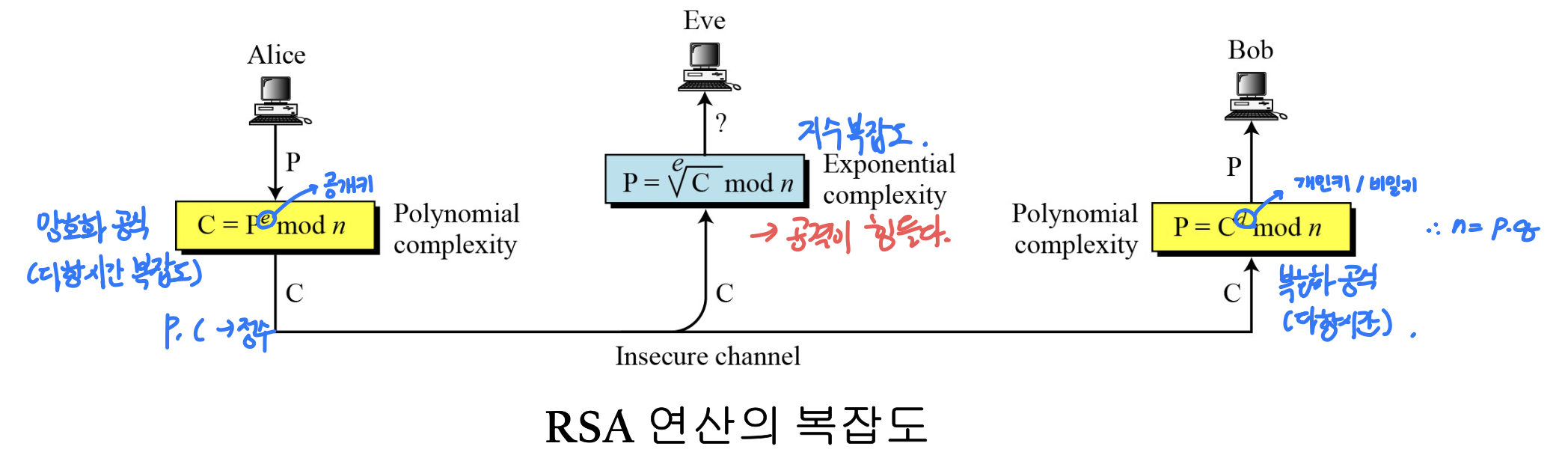
RSA의 수행 절차
- 키 생성: 군 G에서 공개키와 비밀키 생성
- 암호화: 환R에서 공개키 (e,n)을 사용해 평문을 암호화
- 복호화: 환R에서 비밀키 d를 이용해 암호문을 복호화
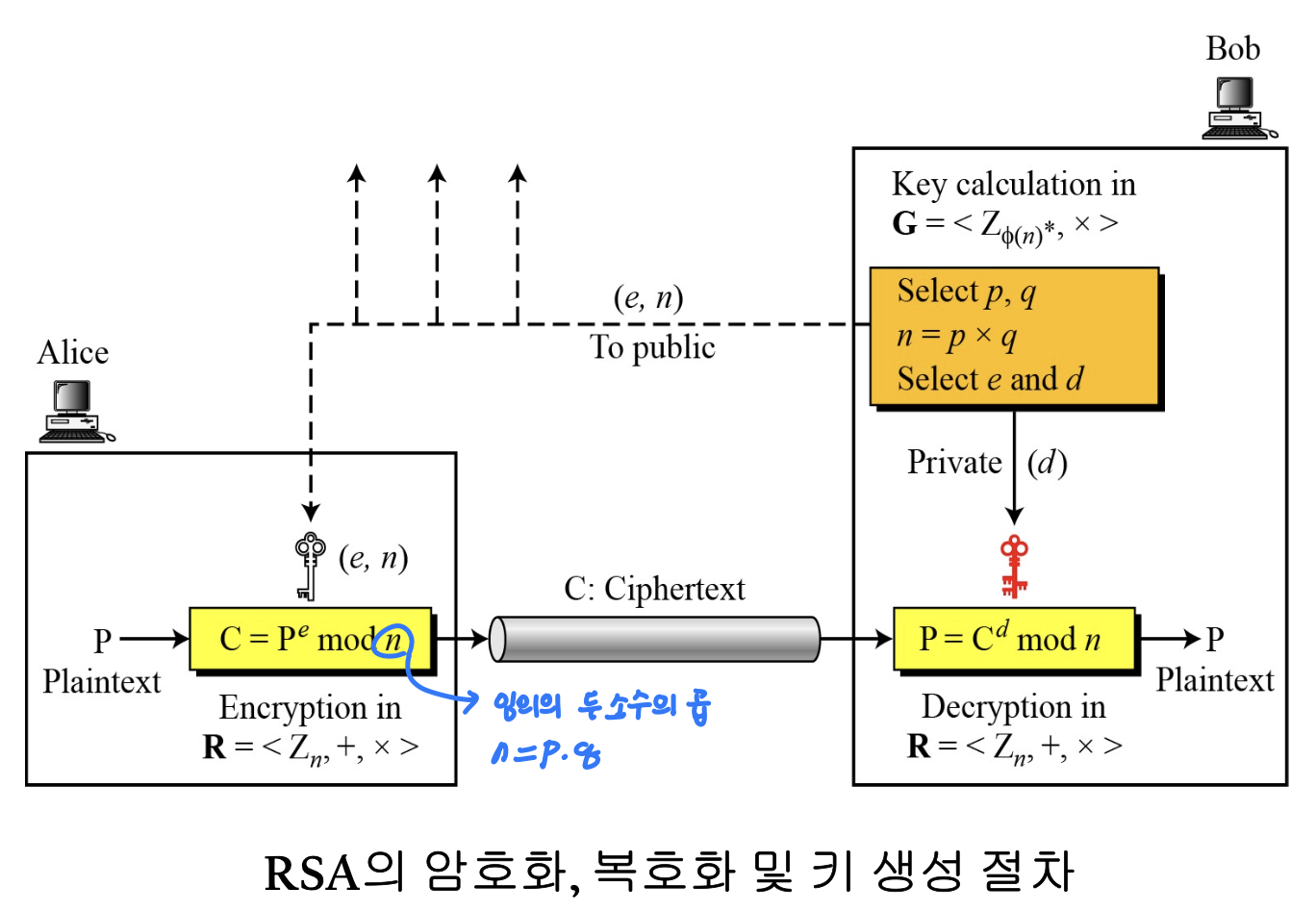
- 암호화
- C ≡ P^e mod n
- 공개키 (e, n)
- 복호화
- P ≡ C^d mod n
- 비밀키 d
RSA에서 사용되는 대수 구조
- 암호화 및 복호화에서 사용되는 환: R = <Zn, +, x>
- 키 생성에서 사용되는 군: G = <Z'∅(n), x>
- 추가 사항: ∅(n) = (p-1) x (q-1)
암호화
- 공개키 (e, n)을 사용하여 수진자에게 메시지를 보낼 수 있음
- 다항식 연산 정도의 복잡도를 가진 알고리즘을 이용해 수행함
- 평문의 크기는 n의 길이보다 작아야 하며, 만약 평문의 길이가 n보다 크다면 평문을 n보다 작은 블록으로 나누어 암호화함
복호화
- 암호화와 마찬가지로 다항식 연산 정도의 복잡도로 계산
- 이때 암호문의 크기는 n보다 작음
RSA 암호화/복호화 예제
- 수신자는 p와 q를 7과 11로 선택해서 n = 7 x 11 = 77 계산함
- 그렇다면 ∅(n) = (7-1) x (11-1) = 60
- 수신자는 Z'60 내에서 두 개의 지수 e와 d를 선택함
- 이때, 만약 e = 13이면 d = 37이 됨 (e x d mod 60 = 1)
Rabin 암호 시스템
개요
- Rabin 암호 시스템은 e와 d가 고정된 값을 갖는 RSA 암호 시스템
- e = 2, d = 1/2
- 암호화: C ≡ P^2 mod n
- 복호화: P ≡ C^(1/2) mod n
Rabin 암호 시스템 개요
- 공개키: n
- 비밀키: 순서쌍(p, q)
- 즉 누구나 n을 이용하여 평문을 암호화할 수 있고, 수신자는 자신이 갖고 있는 비밀키 (p, q)를 활용해 복호화할 수 있음
- 복호화 시 RSA와 Rabin의 차이점
- RSA: 수신자는 d와 n을 간직하고 키를 생성한 다음 p, ∅(n)은 버림
- Rabin: 수신자는 p와 q 값을 반드시 갖고 있어야 함
키 생성
- 두 소수 p와 q는 4k + 1 또는 4k + 3의 형식 보둑 ㅏ능하지만, 4k + 1의 형식일 경우 복호화 과정이 어려워짐
- 따라서 수신자가 쉽게 복호화할 수 있도록 4k + 3의 형식으로 두 소수 p와 q를 선택함
암호화
- 평문 P가 Zn에 속해 있지만 복호화를 쉽게 하기 위해 Z'n으로 한정함
- 암호화 연산은 매우 간단해 성능이 낮은 플랫폼에서도 효과적으로 활용될 수 있음
복호화
- 암호문 C와 개인키 p,q를 활용해 a1, a2, b1, b2를 계산
- (a1, b1), (a1, b2), (a2, b1), (a2, b2) 각각에 대해 중국인의 나머지 정리 알고리즘을 호출해 복호화 수행함
Rabin 암호 시스템의 특징
- Rabin 암호 시스템은 결정적 알고리즘이 아님
- 복호화를 하면 동등함 확률로 4개의 평문 후보가 나타남
- 수진자는 이 4개의 평문 후보 중에서 하나의 진짜 평문을 선택함
- 일반적으로 수신자는 후보 평문 리스트에서 진짜 평문을 쉽게 구별할 수 있음
- Rabin 암호 시스템은 소인수분해 문제와 동치임
Rabin 암호화/복호화 예제
