

DES의 취약성
DES 암호 설계에서의 취약점
- S-박스의 취약점
- P-박스의 취약점
-> 규칙성 - 키의 취약점
- 키의 크기(길이)
- 취약키와 준 취약키
- 취약 가능 키
- 키의 보수
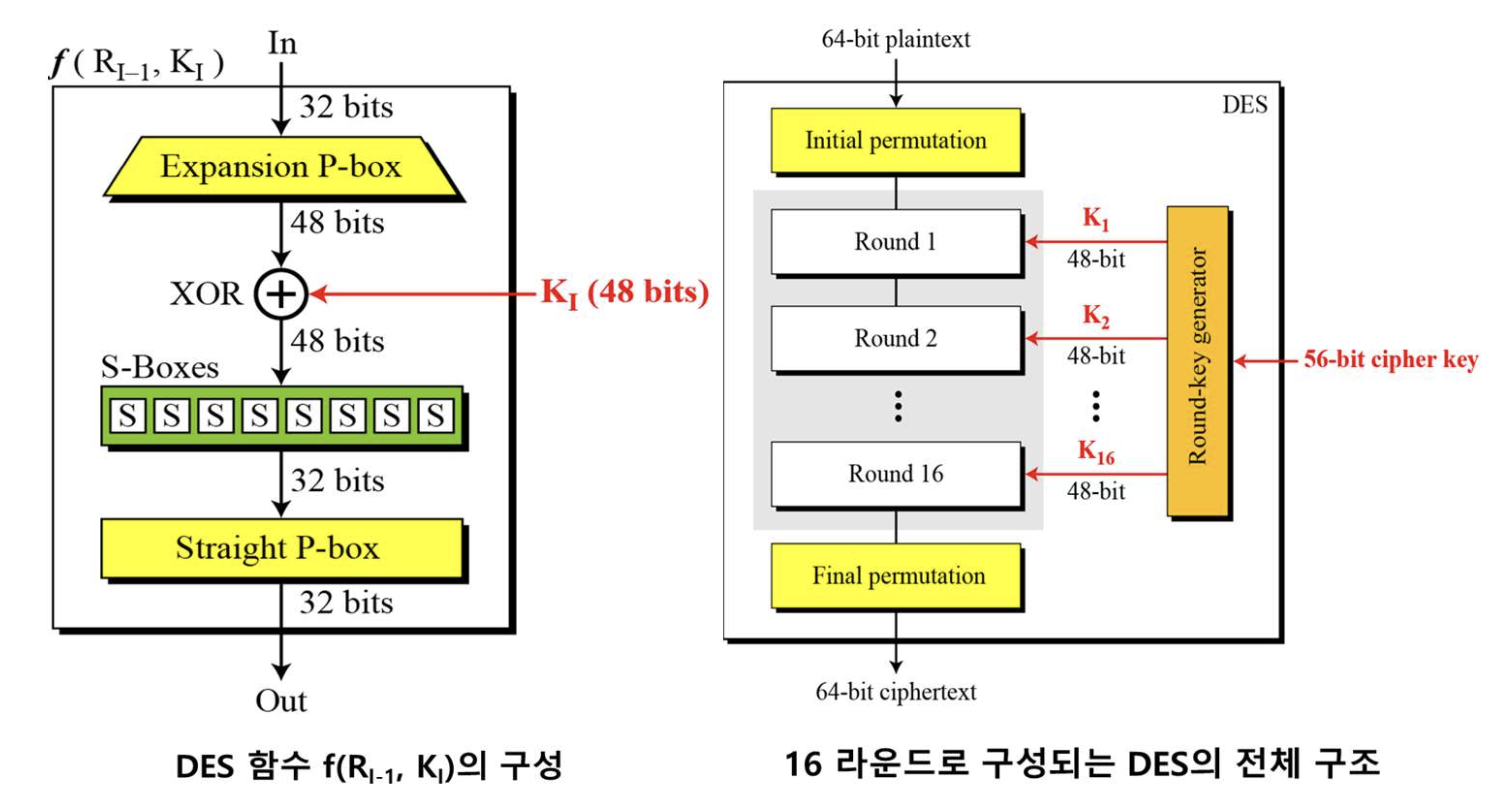
S-박스의 취약점
-> 일련의 규칙성이 존재함
- 4번째 S-박스에서 4비트 출력 비트 중 하위 3개의 출력 비트는 입력 비트 중 일부를 보수로 취함으로써, 첫 번째 출력 비트와 같은 방법으로 얻을 수 있음
- 하나의 S-박스에 특별하게 선택된 두 입력 값은 같은 출력 값을 생성함
- 세 개의 이웃하는 S-박스에 들어가는 입력 비트를 바꾸는 것만으로 하나의 라운드에 대해 동일한 출력 값을 얻을 수 있음
P-박스의 취약점
- DES의 설계자들이 초기 치환과 최종 치환을 사용한 이유가 명확하지 않음
- 초기 치환과 최종 치환은 단순 P-박스이자 키 값이 전혀 사용되지 않는 고정된 규칙이므로 암호의 안전성 향상에 도움이 되지 않음
- DES 함수 내부의 확장 치환(확장 P-박스)에서 4비트 단위로 분할하면 첫 번째와 네 번째 비트가 반복됨 -> 규칙성이 보임
키 크기의 취약점
- DES에서 사용되는 키 = 56비트 (64bit - 패리티 비트 8bit)
- 2^56개의 키에 대한 전수 조사 공격이 가능함
- 하나의 프로세서를 보유한 컴퓨터로 약 2천년 이상의 시간이 필요함
- 병렬 처리가 가능함 100만개의 칩을 가진 컴퓨터를 개발한다고 가정하면,
- 20시간 내에 전수 조사 가능함
- 실제로 1998년에 112시간 안에 DES 키를 찾을 수 있는 특수 컴퓨터가 개발됨
- 네트워크를 이용한 병렬 처리 수행 시
- 1977년 RSA 연구소에서 인터넷에 연결된 3500대의 컴퓨터를 이용하여 120일만에 키를 찾아내는데 성공함.
- 이 경우, 42000명의 회원으로 구성된 비밀집단 -> 10일 안에 키를 찾을 수 있음.
🔑 취약키(Weak Keys)
- 총 2^56개의 키 중에서 4개의 취약키로 정의함
- 취약키란 64비트의 키에서 패리티 제거 연산 이후에
- 모두 0이거나
- 모두 1이거나
- 절반은 0이고 나머지 절반은 1
로 구성되는 56비트의 키를 의미함
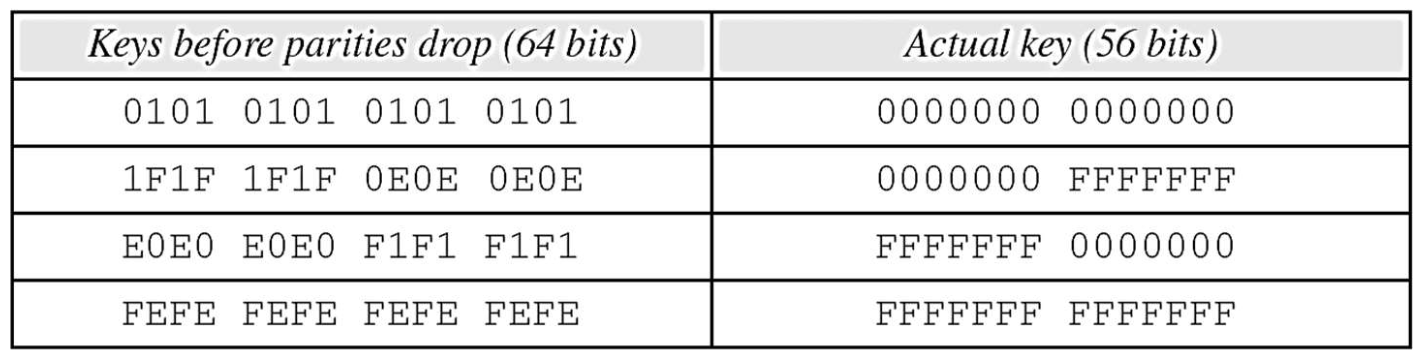
취약키를 가진 이중 암호화와 복호화
- 취약키를 갖고 블록을 암호화하고 그 다음에 같은 취약키를 갖고 그 결과를 암호화하면 원래의 블록이 나옴
- 블록은 두 번 복호화하면 , 이 과정은 같은 본래의 블록을 만들어냄
- 따라서 각 취약키는 Ek(Ek(P)) = P의 역관계임
키를 사용하는 의미가 없음
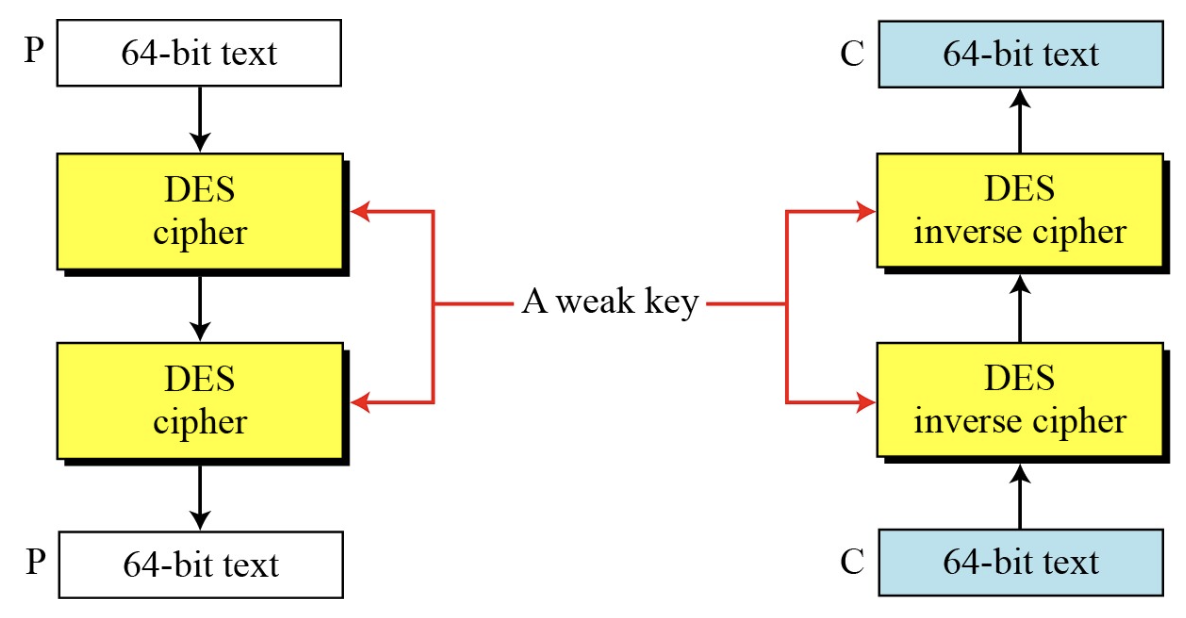
예제1) 취약키의 문제점

🔑 준취약키(Semi-weak Keys)
- DES에는 준취약키라 불리는 6개의 키 쌍이 존재함
- 준취약키는 오직 두 가지의 다른 형태의 라운드키만 생성함
- 각 라운드 키는 8번씩 반복됨
- 하나의 쌍으로 묶인 두 개의 준취약키는 순서만 다를 뿐 동일한 라운드키를 생성함
- 이때 하나 이상의 취약키들의 그룹을 키 클러스터라고 함
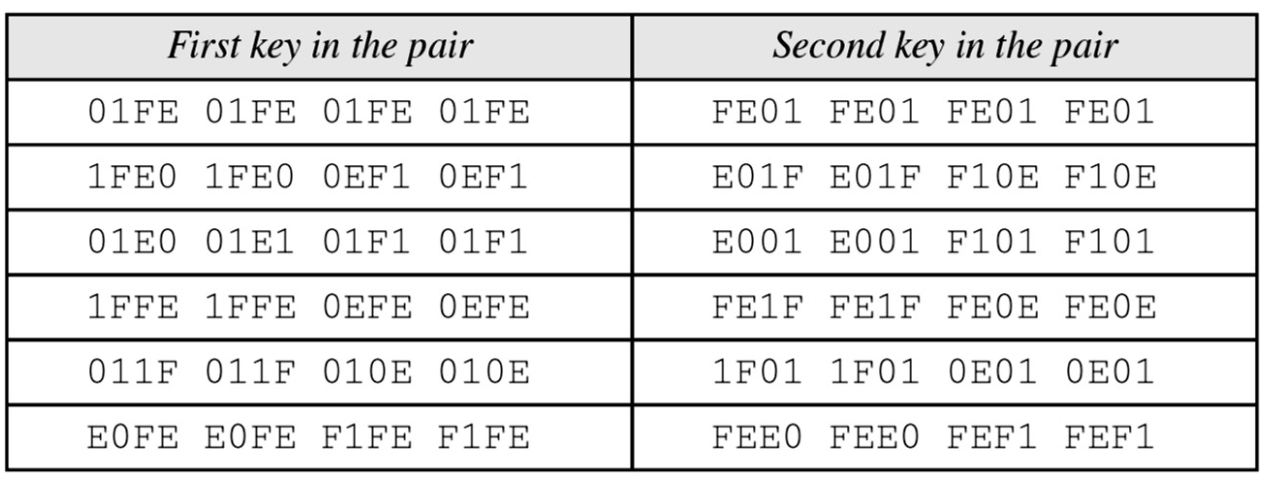
- 이때 하나 이상의 취약키들의 그룹을 키 클러스터라고 함
예제2) 첫번째 준 취약키 쌍으로 생성되는 라운드 키 분석
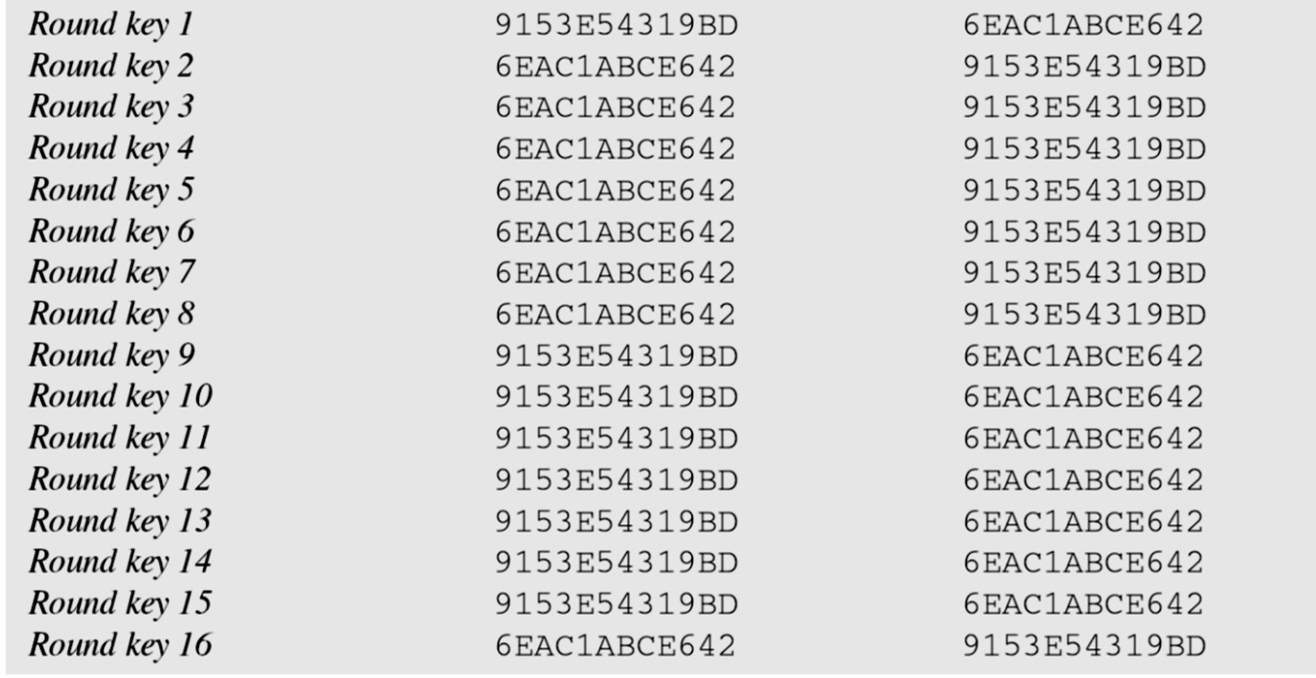
- 각 준취약키에 8개의 같은 라운드키가 존재함
- 첫 번째 준취약키로부터 생성된 라운드 키는 두 번째 준취약키로부터 생성된 라운드 키 16과 같음
- 첫 번째에 있는 라운드 키 2는 두 번째에 있는 라운드 키 15와 같음
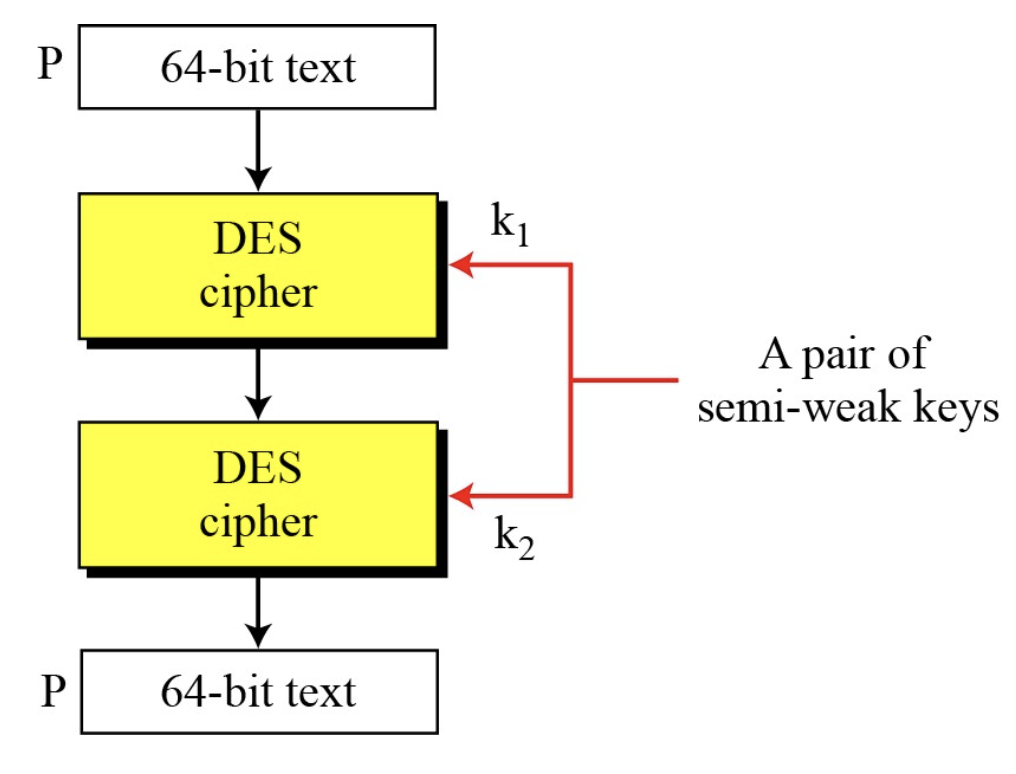
암호화 및 복호화 과정에서의 준 취약키 쌍
- 준취약키 쌍의 키들을 서로 역관계 -> Ek2(Ek1(P)) = P
취약 가능 키 (Possible Weak Keys)
- 총 48개가 존재함
- 4개의 서로 다른 라운드 키를 생성하는 키
- 즉, 16라운드 키는 4개의 그룹으로 나누어지고, 각 그룹은 4개의 동일한 라운드 키로 구성됨
예제3) 취약키, 준취약키 또는 가능한 취약키를 임의로 선택할 확률은?
- DES는 2^56개의 원소로 이루어진 키 집합을 가짐
- 취약키, 준취약키 또는 가능한 취약키의 총 개수는 64 (= 4 + 12 + 48)
- 12 = 6 x 2 -> key pair 6개 = 키 12개
- 이런 키들이 선택될 확률은 8.8 x 10^(-16)이기 때문에, 결과적으로 위의 키들이 선택되는 것은 불가능
키 보수 (Key Complement)
- 크기가 2^56인 키 집합에서 원소 중의 절반은 나머지 절반의 보수로 표현됨
- 키의 보수는 키에서 각 비트를 거꾸로 함으로써(0 -> 1, 1 -> 0) 생성됨
- 키 보수는 어떻게 암호 해독의 작업을 간단하게 하는가?
- 공격자는 키의 전수조사 공격을 수행하기 위해, 가능한 후보키들 중의 절반(= 2^55 가지)만을 사용하면 됨
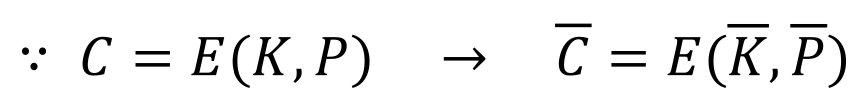
- 즉, 키와 평문에 모두 보수를 취하여 암호화하면, 원래의 암호문의 보수인 암호문을 얻게 됨
- 따라서 공격자는 모든 2^56개의 가능한 키들을 모두 검사하지 않고, 절반만 검사하고, 나머지 키에 대해서는 보수의 성질을 이용하여 값을 얻을 수 있음
예제4) 보수 키의 성질
- 대응되는 암호문을 얻기 위해 임의의 키와 평문을 사용함
- 그 다음에, 원본 키와 평문에 보수 연산을 취하면, 아래와 같이 이전에 얻은 암호문에 대한 보수를 얻게 됨
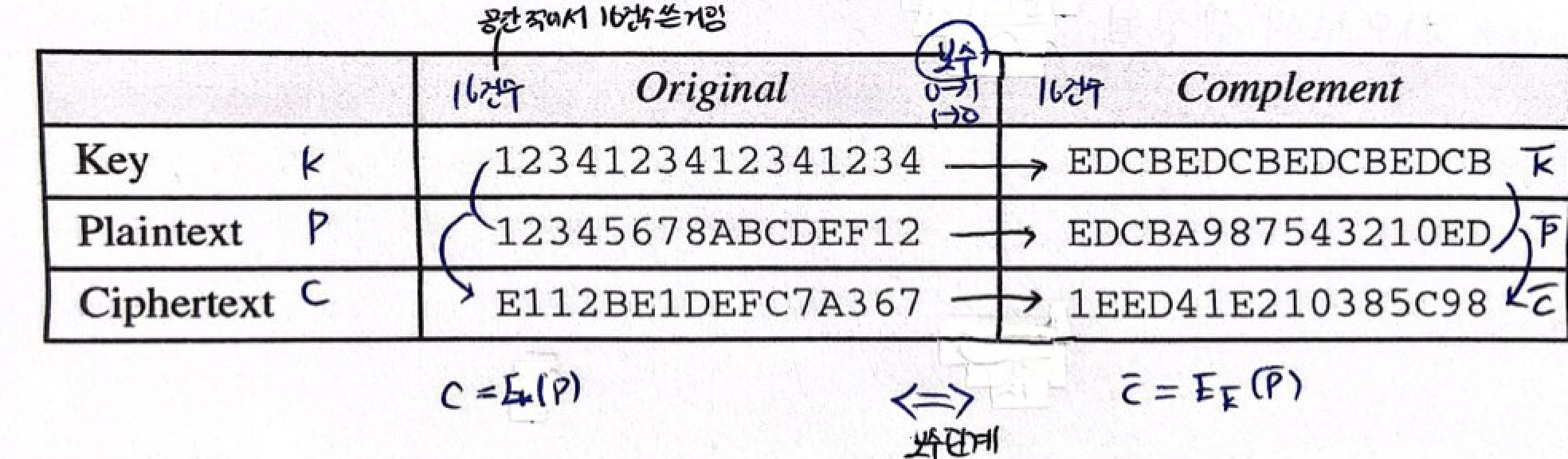
- 2^56 / 2 = 2^55 : 나머지는 분석된 결과를 보수화하면 얻어낼 수 있음
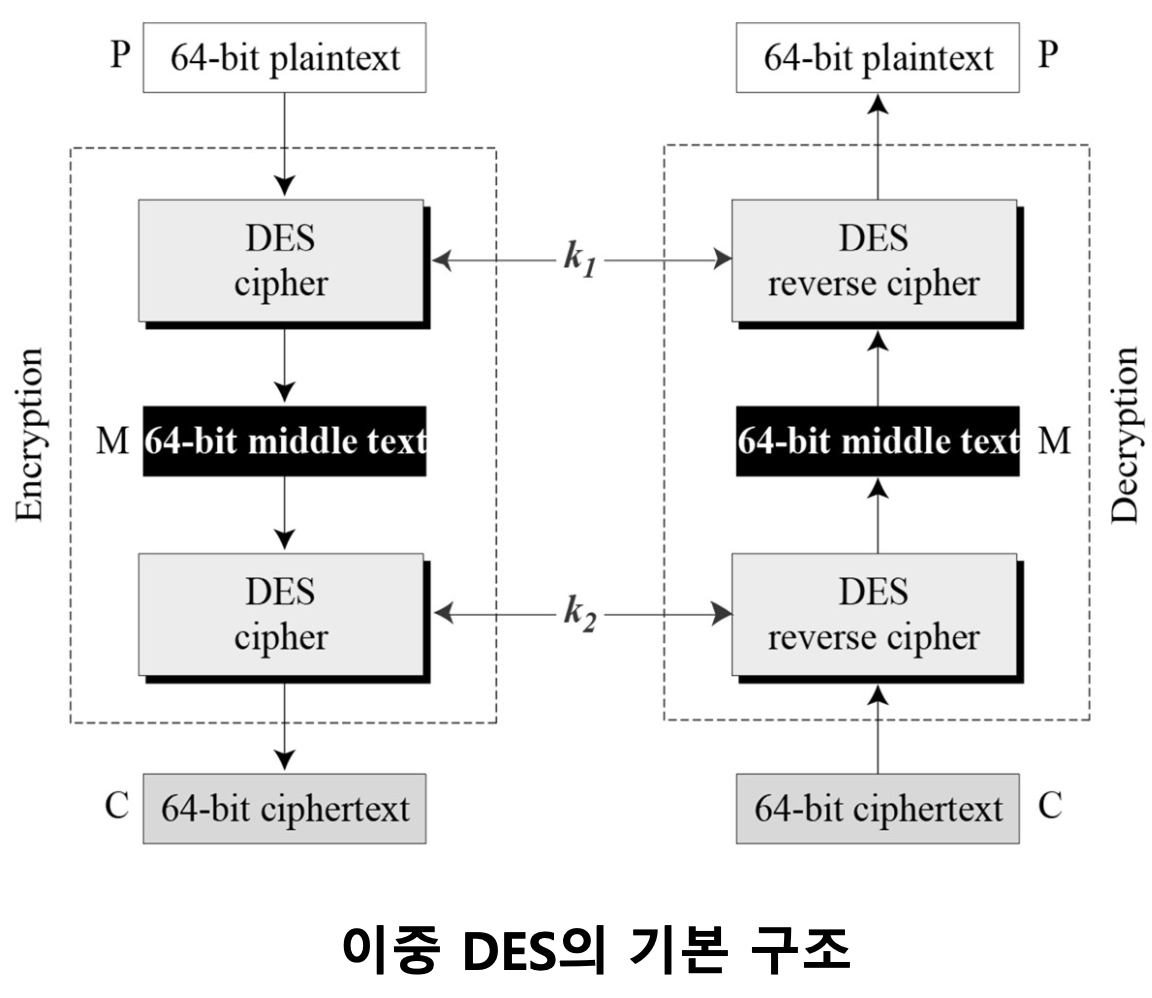
이중 DES와 삼중 DES
이중 DES(Double-DES)의 주요 특징
- 주어진 평문에 대해 두 번 암호화 수행
- 주어진 암호문에 대해 두 번 복호화 수행
- 각각의 암호화 과정에서 서로 다른 두 개의 키를 사용
- 그러나 기지 평문 공격 방법 중 하나인 중간 일치 공격에 취약함
키 분석할 때 경우의 수가 많길 기대함
- DES의 키의 길이 = 56비트
- 이 경우, 단순하게 생각하면 이중 DES는 키를 탐색하지 위한 탐색 횟수가 2^56변 (=하나의 DES에 대응)에서 2^112번(=두 개의 DES에 대응)으로 증가하는 것으로 이해할 수 있음 -> 키를 두 개 사용하므로
- 그러나 중간-일치 공격과 가은 기지 평문 공격을 사용하면 2^112번이 아닌 2^57번으로 단지 약간의 향상만(=기존의 2배) 수행됨을 증명할 수 있음
알고리즘을 늘린 만큼 키 분석 경우의 수가 늘어나지 않음
중간-일치 공격(Meet-in-the-Middle Attack)
- 처음 암호화 할 때 중간 테스트와 복호화 할 때 중간 텍스트의 값이 같아야 함
- M = Ek1(P) and M = Dk2(C) 만족해야 함
- 공격자가 기지 평문 공격을 수행하여 이전의 쌍 P와 C를 가로챘다고 가정함
- 첫 번째 관계에 기반해 공격자는 k1의 모든 가능한 값(2^56)을 사용해 C를 복호화하고 M에 대해 얻은 모든 값을 기록함

