[백준]2749번 피보나치 수3

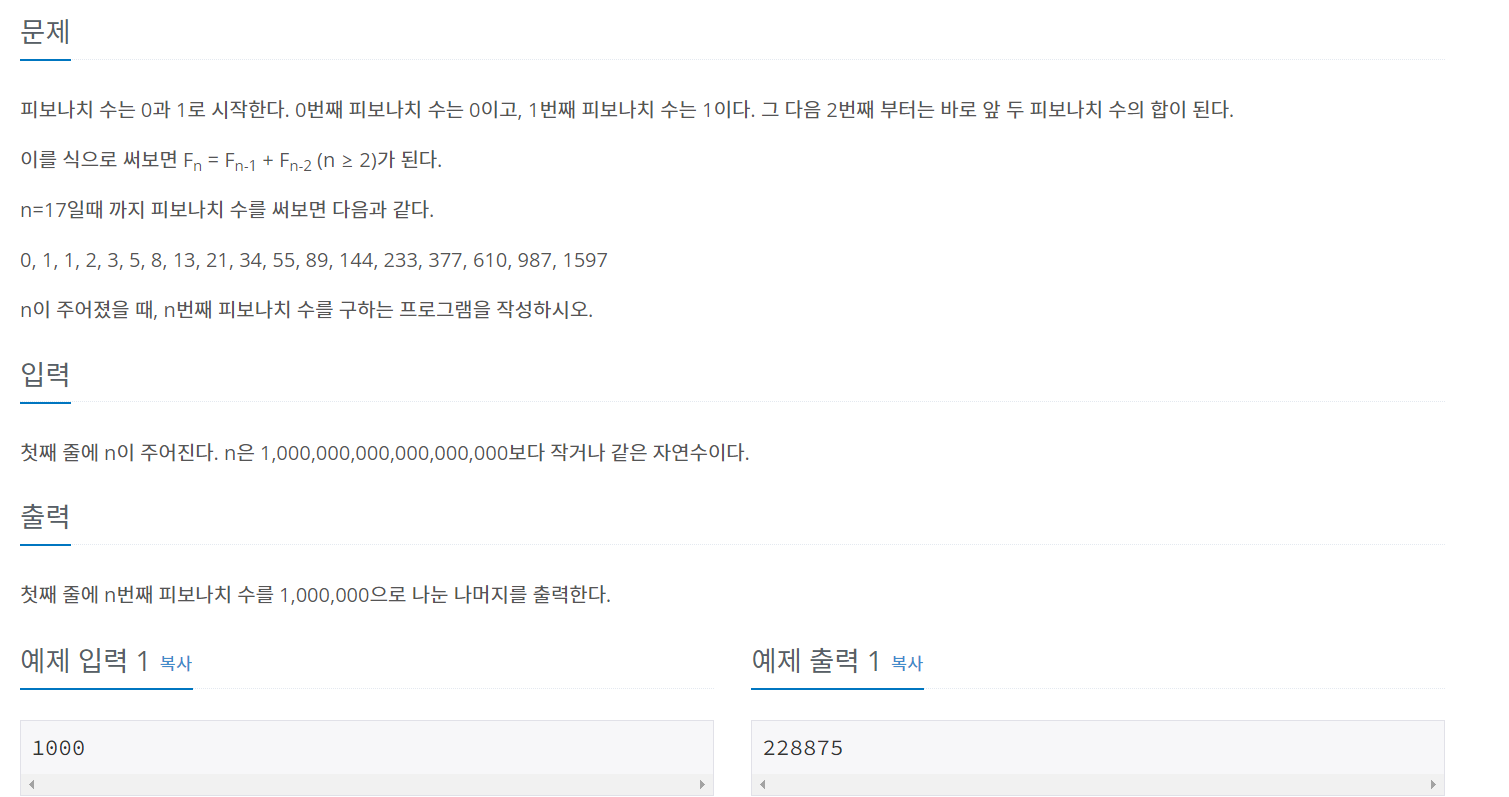
1, 2 버전과 동일한 문제이지만 1,000,000으로 나눈 나머지를 출력하면 됨. 여기서 분할 정복 (모듈러 정리)를 사용해서 해결하면 됨.

그러나 여기서 추가적인 개념이 필요했음.

피사노 주기

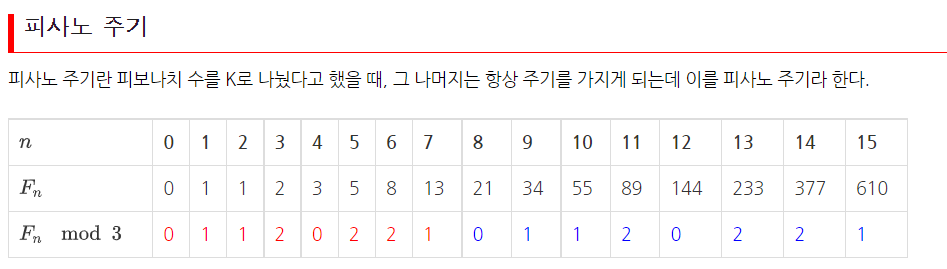
문제에서 n이 1,000,000으로 나눈 나머지이기 때문에 이 피사노 주기를 p라고 하면 n%p번째 피보나치 수를 1,000,000으로 나눈 나머지와 같다.

M = 10^k일 때 k>2라면, 주기는 항상 15x10^(k-1)임.

이에 따라 주기는 15 * 10^(6-1) 이므로 n번째 피보나치 수를 1,500,000으로 나눈 나머지를 1,000,000으로 나눈 것과 같음.

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        long n = Long.parseLong(br.readLine());
        int P = 1500000;
        n %= P;

        long arr[] = new long[P];
        arr[0]= 0;
        arr[1] = 1;

        for(int i = 2; i <= n; i++) {
            arr[i] = (arr[i-1] + arr[i-2]) % 1000000;
        }

        System.out.println(arr[(int)n]);

    }
}

메모제이션 기법을 사용하지 않으니 시간초과, 메모리초과가 발생했다.
런타임 에러는 static 변수를 없애고 지역 변수로 만들어주니 해결되었다.