백준

물건을 배낭에 담을 때1\. 현재 배낭의 허용 무게보다 넣을 물건의 무게가 더 크면 넣지 않음2\. 다음 중 더 나은 가치를 선택해 넣음 2-1) 현재 넣을 물건의 무게만큼 배낭에서 빼고 현재 물건을 넣음 2-2) 현재 물건을 넣지 않고 이전 배낭 그대로 가지고 감 현

최대/최소 우선순위 큐의 크기가 같으면 최대 큐에 삽입하고 같지 않다면 최소 큐에 삽입함.최대/최소 우선순위 큐가 비어있지 않고, 최대 큐의 루트값이 최소 큐의 루트값보다 크다면 두 값의 자리를 바꿔줌.최대 우선순위 큐의 루트값을 출력함1\. 리스트 사용시간초과2\.

11401번 이항 계수3 문제를 해결하기 위해 이 문제를 먼저 풀어보았다.이 문제를 해결하기 위해서는 지수 법칙과 모듈러 성질이 필요하다.지수 법칙a^(m+n) = a^m \* a^n모듈러 성질(a b) mod C = (a mod C \* b mod c) mod C

이 문제를 해결하기 위해서는 모듈러 연산과 페르마의 소정리 개념이 필요함먼저 이항 계수를 구하는 방법은 이와 같다.문제에서 주어지는 입력은 너무 크기 때문에 결국 모듈러의 연산 공식을 활용해야한다.여기서 중요한 점은 모듈러 연산에서 나눗셈 연산이 없다는 것이다!즉, 나

행렬의 곱을 구해서 분할 정복 (지수 법칙, 모듈러 정리)를 통해 해결할 수 있음. 그러나 행렬의 곱을 구하는 방법에서 문제가 발생했음.행렬의 곱을 구하는 것까지는 성공했으나 오류가 발생함.원인은 모듈러 정리를 적용해주지 않았기 때문임.long 타입의 숫자가 아닌 행렬

1\. 재귀함수시간초과2\. 반복문

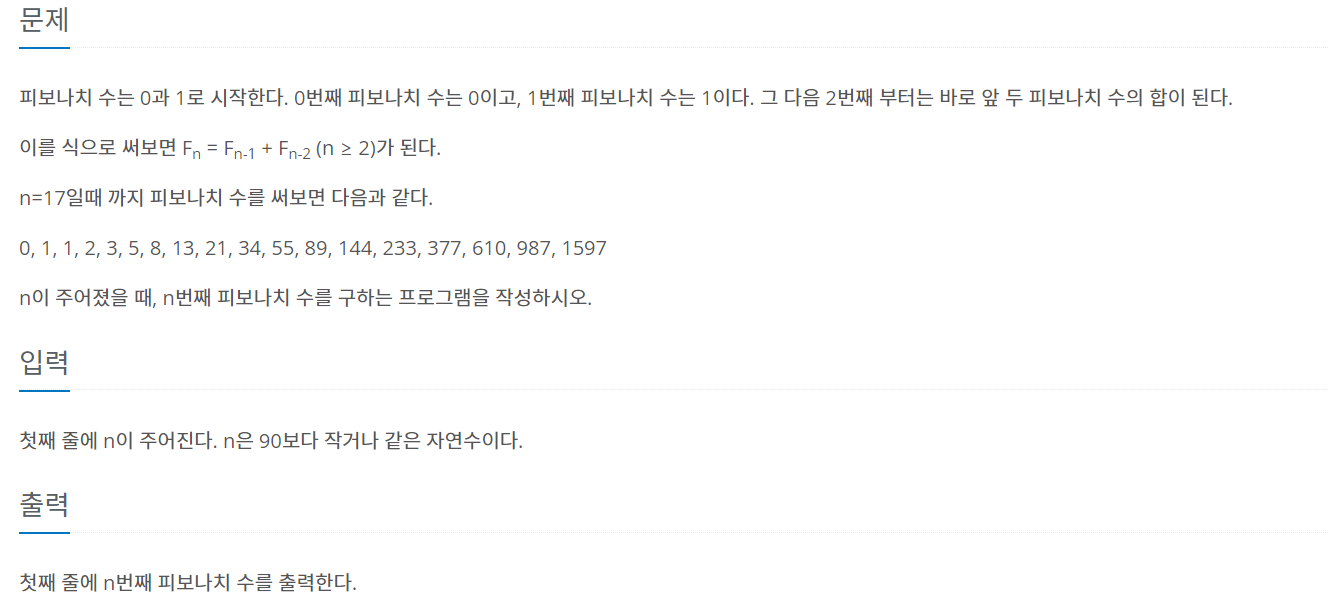
피보나치 수1 문제와 동일한 조건이라 똑같은 코드를 제출했지만 틀렸다.문제 유형을 찾아보니 동적 프로그래밍 유형이었다.메모제이션 기법을 사용하여 해결했다.문제를 제출했을 때 바로 맞히지는 못 했는데 그 원인은 int형 배열을 사용해서 그런 것이라고 예상됨.

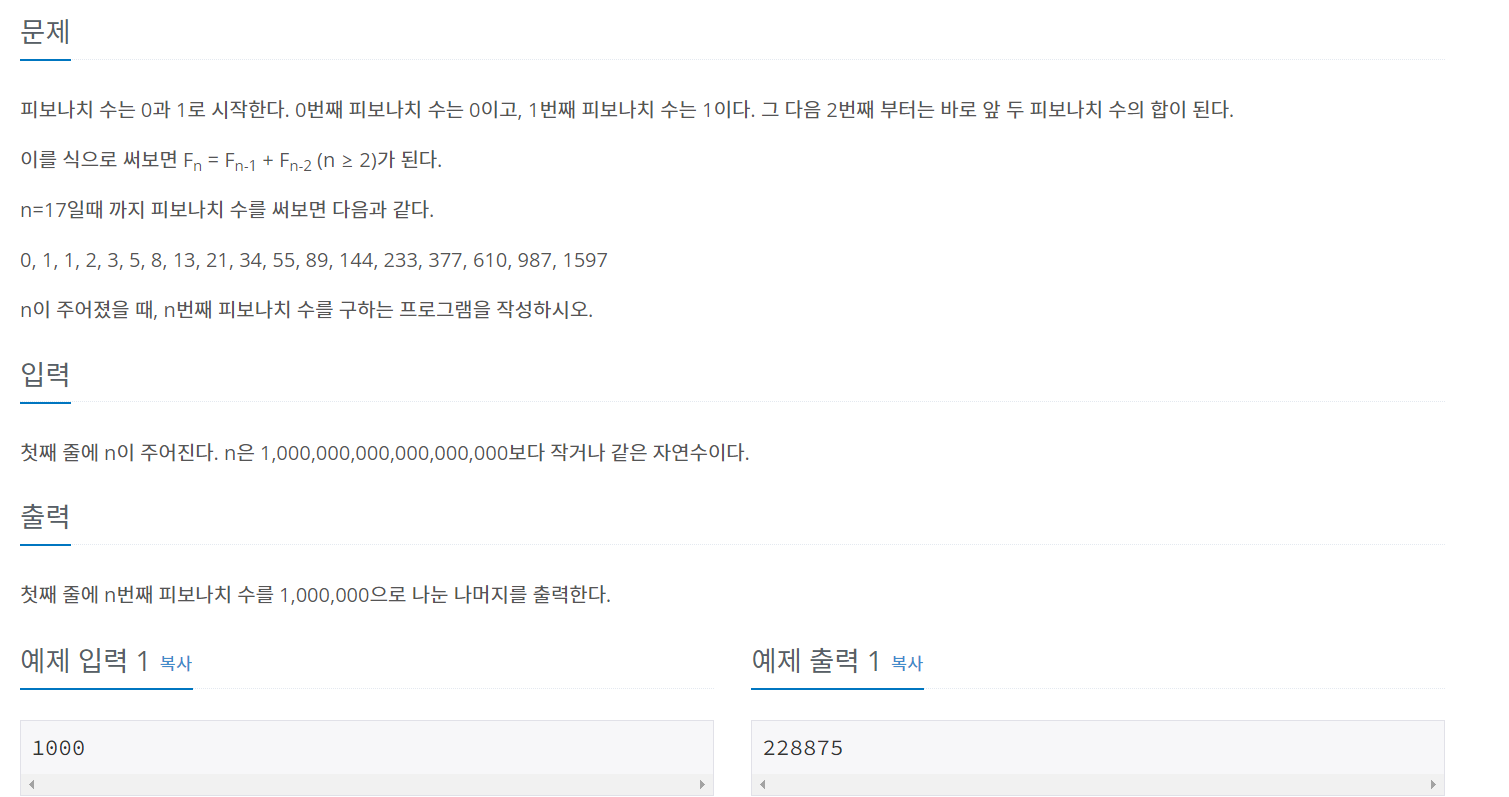
1, 2 버전과 동일한 문제이지만 1,000,000으로 나눈 나머지를 출력하면 됨. 여기서 분할 정복 (모듈러 정리)를 사용해서 해결하면 됨.그러나 여기서 추가적인 개념이 필요했음.문제에서 n이 1,000,000으로 나눈 나머지이기 때문에 이 피사노 주기를 p라고 하면

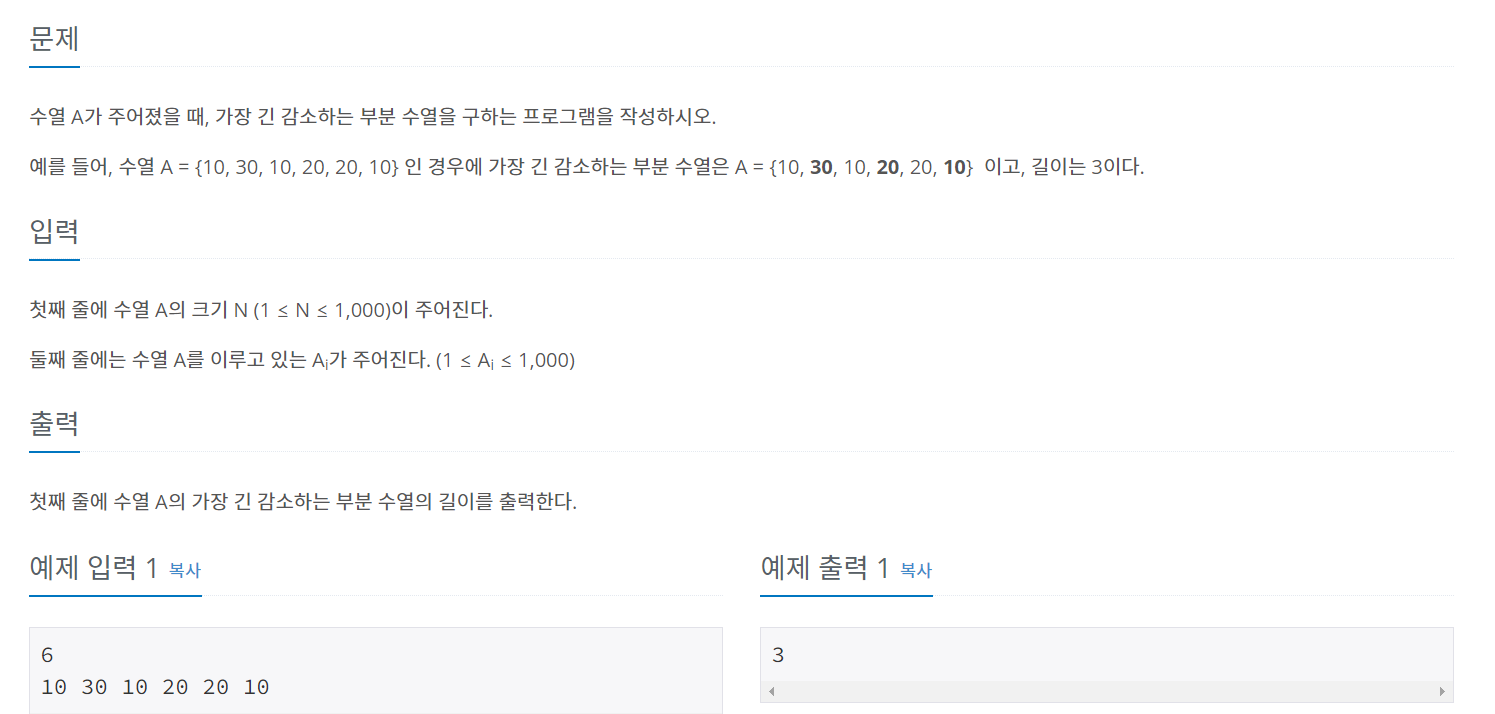
처음에 접근할 때는 이런 방식으로 접근을 했다.근데 해결이 안 되고 어떻게 해야할지 몰라서 구글링 해보았음우선 메모제이션 기법 사용dpn이 n번째 수로 끝나는 부분수열 중 가장 긴 것의 길이를 의미함n번째 수로 끝나는 부분 수열에서는 n번째 수가 마지막이기 때문에 n-

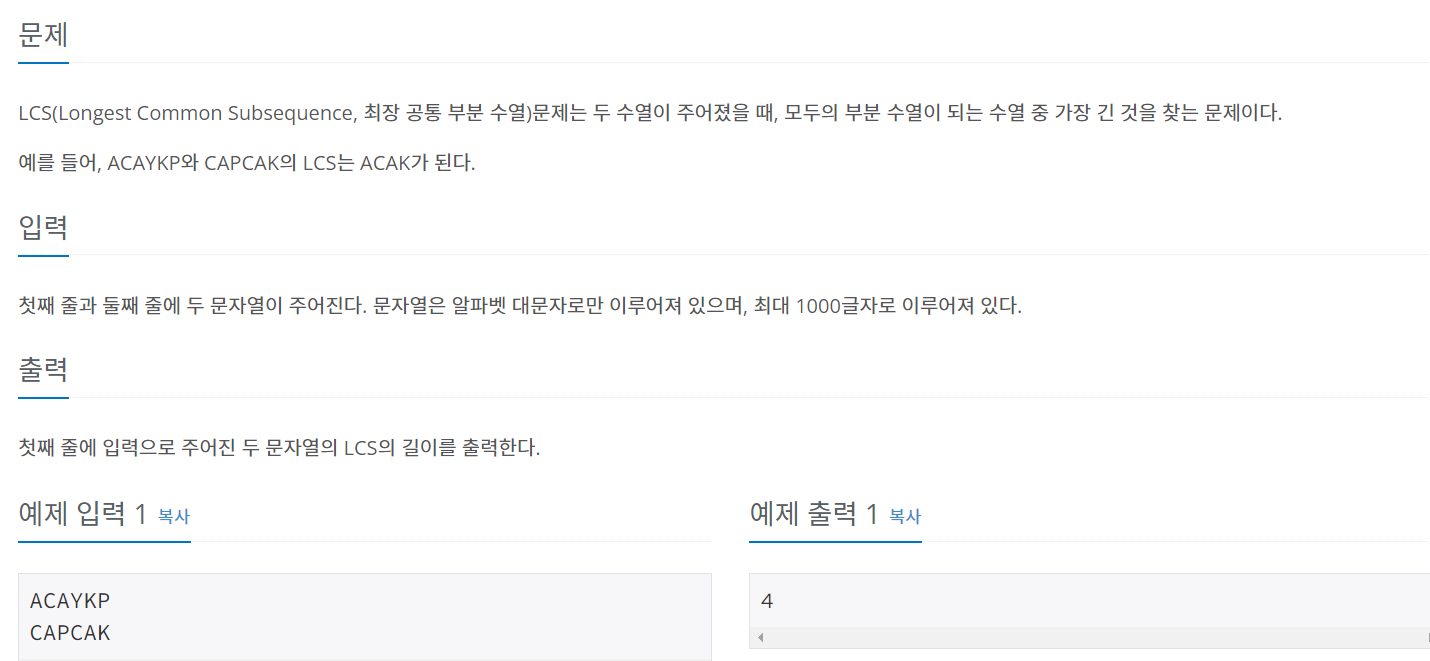
LCS 최장 공통 부분 수열 문제문자열 a, b의 한 글자씩 비교한다.두 문자가 다르다면 lcsi-1와 lcsi중 큰 값을 저장한다.두 문자가 같다면 lcsi-1 +1을 저장한다.위 과정을 반복한다.<2>현재 문자를 비교하는 과정 이전의 최대 공통 부분수열은 계속

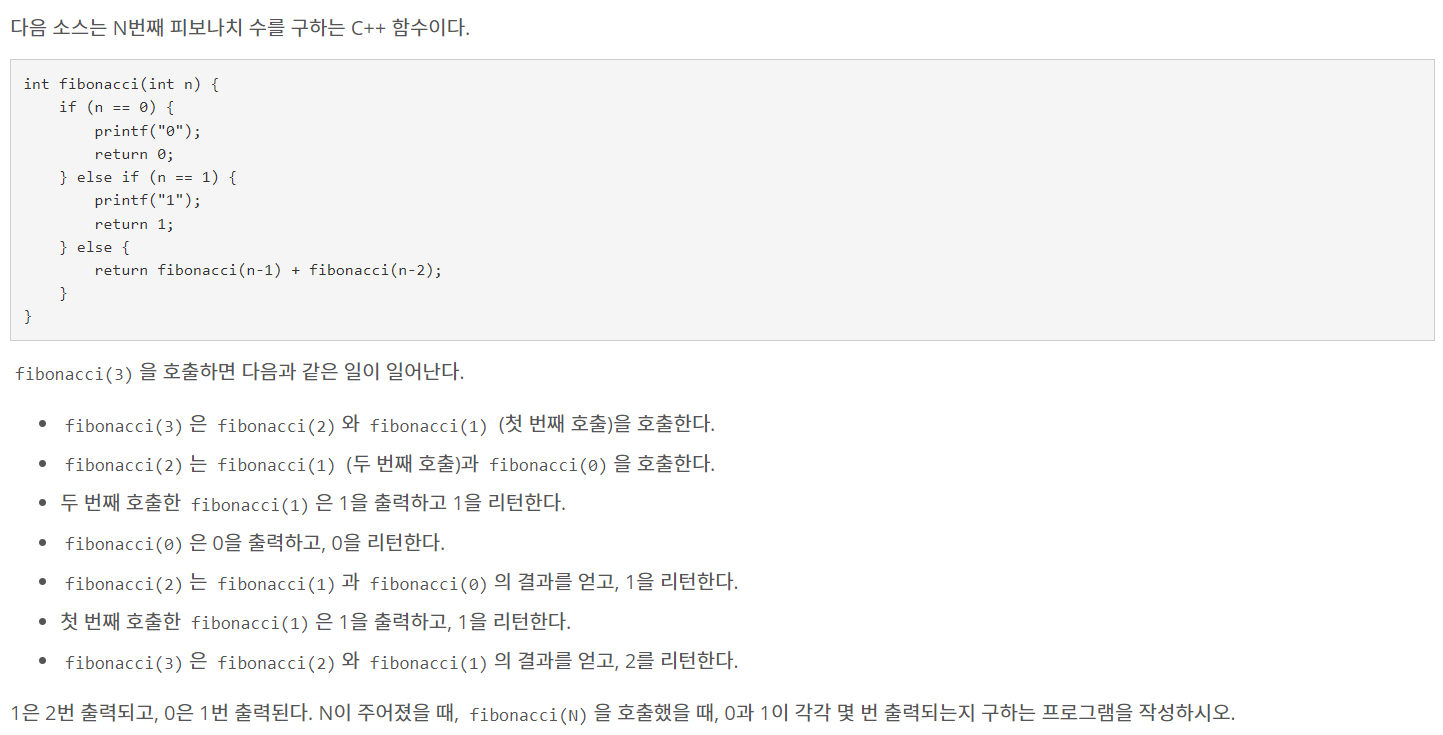
풀이 과정처음에는 재귀함수로 해결하려고 했으나 점점 복잡해지는 것 같아서 풀이 방향을 바꿨다. 이런 문제를 해결할 때 점화식이 중요하다. 반복되는 부분을 찾아야한다. 아래 부분에서 볼 수 있듯이 n에 대한 0의 호출은 n-1의 1 호출과 동일하고 n에 대한 1의 호출은