[Leetcode/C++] 121_Best Time to Buy and Sell Stock

문제는 다음과 같습니다.

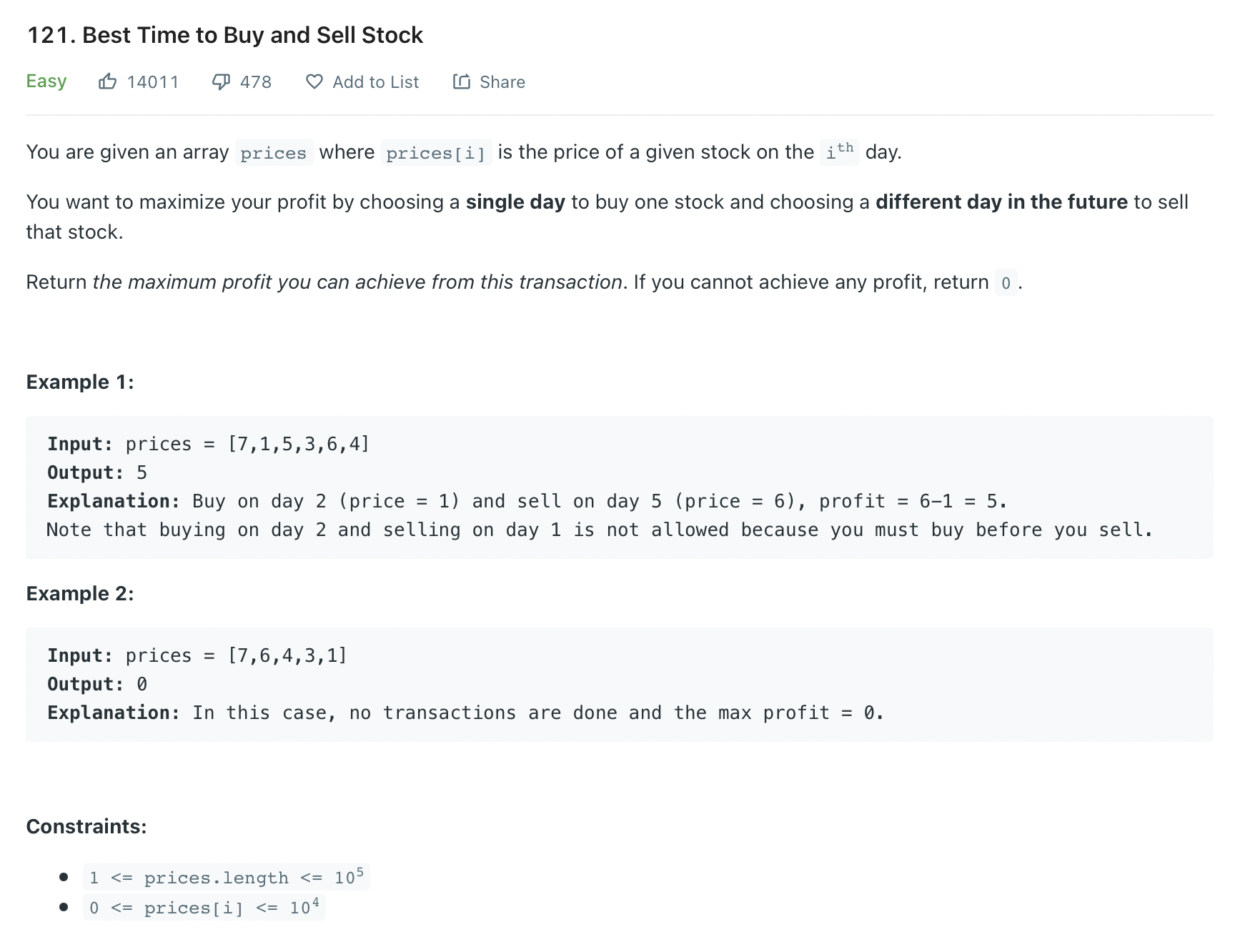
이번 스터디 문항중 하나가 이 문제의 업그레이드 버전이더라구요? best time to buy and sell stock2 였나 그런데 작년에 이 문제를 풀었던 기억 이 있어서 복습차원에서 다시 한 번 풀어보았습니다.

제가 생각한 이 문제의 조건은 다음과 같습니다.

1. 주식을 사는 것 먼저 -> 이후에 팔기

2. O(n)의 시간복잡도 안에 구하려면, 주식의 가장 minimum인 buy_cost를 계속해서 갱신해서 구하고, 이후에 이익인 profit도 마찬가지로 갱신해나간다.

3. profit = max(profit, prices[i]-buy_cost)로 이익도 계속해서 갱신해서 구한다.

4. 따라서, for문안에서 buy_cost(사는 가격)을 먼저 이후에 profit(이익)을 계산한다.

제 전체 코드는 다음과 같습니다.

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int profit = 0;
        int buy_cost = prices[0];
        
        for(int i=1; i<prices.size(); i++){
            buy_cost = min(buy_cost, prices[i]);
            profit = max(profit, prices[i]-buy_cost);
        }
        return profit;
    }
};

이 문제를 dp를 이용해서도 풀어보았습니다.
벡터 dp를 선언했고,
dp[i]에는 i번째 가격에 주식을 팔았을 때 얻을 수 있는 최대 수익을 저장해놓았습니다.
즉, dp[i] = prices[i]-buy_cost 입니다.
이때의 buy_cost에는 i까지의 가격 중 최솟값이 저장되어 있습니다.

전체 코드는 다음과 같습니다.

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int buy_cost = prices[0];
        vector<int> dp;
        dp.push_back(0);
        
        for(int i=1; i<prices.size(); i++){
            buy_cost = min(buy_cost, prices[i]);
            dp.push_back(prices[i]-buy_cost);
        }
        sort(dp.begin(), dp.end());
        return *(dp.end()-1);
    }
};

또한 이 문제를 priority_queue를 이용해서도 풀어보았습니다.
계속해서 갱신되는 이익의 "최댓값"을 구하는 문제이기에, max heap을 이용해서도 풀 수 있다고 생각했기 때문입니다.

시간복잡도는 O(nlogn)입니다.

전체 코드는 다음과 같습니다.

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int buy_cost = prices[0];
        priority_queue<int> pq;
        pq.push(0);
        
        for(int i=1; i<prices.size(); i++){
            buy_cost = min(buy_cost, prices[i]);
            pq.push(prices[i]-buy_cost);
        }
        
        return pq.top();
    }
};