
문제는 다음과 같습니다.
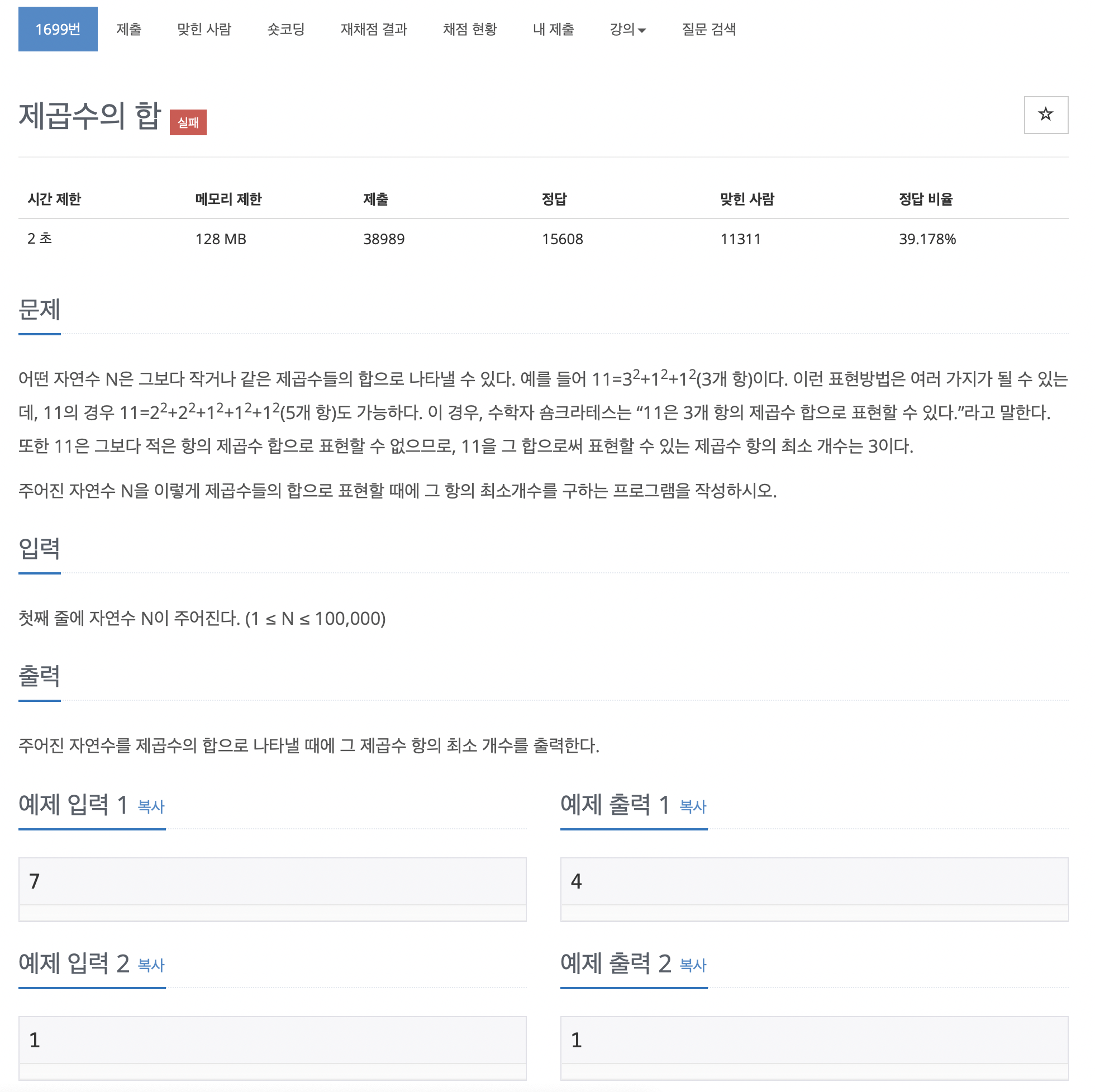
일단, 여러번 시도했지만 실패했던 문제입니다.
틀린것도 나중에 힌트를 얻고나서 왜 틀렸는지 알게되었습니다. ㅋㅋㅋㅋ
분명 쉬워보였는데.. 틀렸습니다🥺
제가 푼 풀이는 다음과 같습니다.
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n, i=1, min_cnt=100000;
cin>>n;
while(i*i<=n){
i++;
if((i+1)*(i+1)>n) break;
}
// i는 쓸 수 있는 최대 제곱수: 1~i까지
for(int j=i; j>=1; j--){
int N=n;
int tmp=0;
int k=j;
while(N>0 && k>=1){
while(N>=k*k && k>=1){
N-=k*k;
tmp++;
}
k--;
}
min_cnt=min(min_cnt, tmp);
}
cout<<min_cnt<<endl;
return 0;
}제가 풀었던 풀이 방식은 다음과 같습니다.
먼저, 뺄 수 있는 최대의 제곱수를 구합니다.
그리고 그 수부터 시작해서 뺄 수 있는 경우의 수만큼 빼고 그 때의 최소 항의 개수를 구합니다,
그리고 최대의 제곱수에서 -1씩 빼서 그 다음 제곱수부터 시작해 경우의 수를 구합니다.
예시로 11을 든다면
11의 최대 제곱수는 3입니다.
그래서 첫 번째 경우에는 => (3x3)+(1x1)+(1x1)=11 이어서 항의 수는 3
두 번째 경우에는 => (2x2)+(2x2)+(1x1)+(1x1)+(1x1)=11 이어서 항의 수는 5
마지막 경우에는 => (1x1)...(1x1)=11 이어서 항의 수는 11입니다.
그래서 최소인 3을 구하게 되는데요,
"즉 시작하는 가장 큰 제곱수를 뺄 수 있을 만큼 빼게 되는 게 이 문제를 틀린 이유였습니다."
예시로 숫자 43을 예로 들면
43 = (43 - 2²) + 2² = …
= (43 - 3²) + 3² = …
= (43 - 4²) + 4² = …
= (43 - 5²) + 5² = 18 + 5² -> 18은 3² + 3² = 2개의 최소 항으로 표시 -> 총 항의 갯수 3개
43 = 18 + 5² = 3² + 3²+5² (3개)
= (43 - 6²) + 6² = 7 + 6² -> 7은 1² + 1² + 1² + 2² = 4개의 최소 항으로 표시 -> 총 항의 갯수 5개
43 = 7 + 6² = 1² + 1² + 1² + 2²+6² (5개)
위의 예시처럼, 더 큰 제곱수를 뺀다 해도, 반드시 최소 항의 갯수를 구한다고 보장할 수 없습니다.
43에서 36을 뺐을 때가 아닌, 25를 뺐을 때 최소 항의 갯수 3개를 가집니다.
따라서 단순하게 자연수 N보다 작은 제곱수들 중 가장 큰 것으로만 빼서 계산한다면 틀리게 됩니다.
해답에서는 dp배열을 이용하여 구했는데요,
점화식의 원리는 다음과 같습니다.
N을 최소 제곱수의 합으로 나타내는 경우의 수를 dp[N]에 저장한다고 하면,
dp[N] = i^2 + dp[N-(i^2)]
로 나타낼 수 있습니다.
즉 i는 0부터 ~ i*i<=N 까지 가능하며,
N은 i의 제곱 + dp[N-(i^2)] 의 수로 표현할 수 있기 때문입니다.
즉, 1부터 n까지의 수를 최소 제곱수를 이용해 나타낼 수 있는 경우의 수를 bottom-up방법으로 구해야합니다.
먼저, 0부터 입력받은 n까지의 수를 dp[i]=i; 로 (초기화를 제곱수 1로만 나타낸 경우) 초기화한 후에
그리고 j를 1부터 j*j<=n까지 돌려, 그 중에서도 최소인 min을 찾으면 됩니다.
위에서 설명한 핵심 코드는 다음과 같습니다.
for(int i=1; i<=n; i++){
dp[i]=i;
for(int j=1; j*j<=i; j++){
dp[i]=min(dp[i], dp[i-j*j]+1);
}
}그리고 전체 코드는 다음과 같습니다.
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n; int dp[100001]={0, };
cin>>n;
for(int i=1; i<=n; i++){
dp[i]=i;
for(int j=1; j*j<=i; j++){
dp[i]=min(dp[i], dp[i-j*j]+1);
}
}
cout<<dp[n]<<endl;
return 0;
}2월 8일 화요일 복습)
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int dp[100001]={0, };
int n; cin>>n;
for(int i=1; i<=n; i++){
dp[i]=dp[i-1]+1;
for(int j=2; j*j<=i; j++){
dp[i]=min(dp[i], dp[i-j*j]+1);
}
}
cout<<dp[n]<<"\n";
return 0;
}