[백준/C++] 1932번_정수 삼각형

문제는 다음과 같습니다.

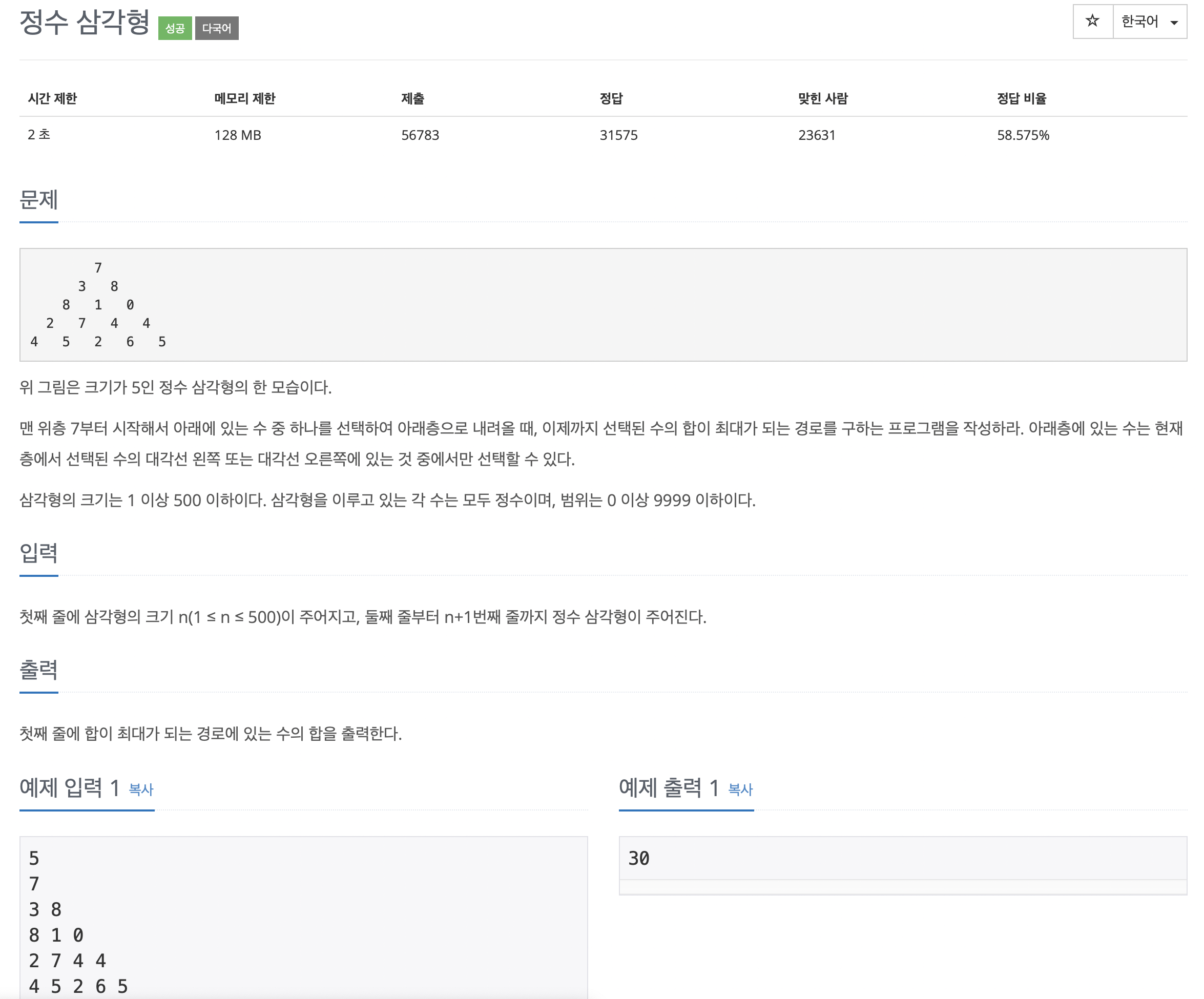
전형적인 DP문제이구요,
제가 생각한 핵심은 삼각형의 맨 위에서 한줄 한줄 내려갈때마다
그 줄에서의 최댓값을 계속해서 갱신해나가면 됩니다.

이때 최댓값을 구할 때 경우가 두 가지로 나뉩니다.

1. 한 줄에서의 양 끝 값일때

즉 아래와 같은 경우입니다.

이때에는 최댓값을 구할 필요 없이 이전의 v[i]+tmp 를 더한 값이 최대가 됩니다.

2. 가운데에 있는 값일 때 (1의 경우 제외한 나머지)

이 때의 최댓값은 바로 위에서 갱신한 벡터 v에서
(그리고 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있으므로)
max(v[i-1], v[i])+tmp 의 값이 최대가 됩니다.

전체 코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    vector<int> v; vector<int> t;
    int n, tmp;
    cin>>n;
    cin>>tmp;
    v.push_back(tmp);

    for(int i=1; i<n; i++){
      for(int j=0; j<=i; j++){
        cin>>tmp;
        if(j==0) t.push_back(v[j]+tmp);
        else if(j==i) t.push_back(v[v.size()-1]+tmp);
        else t.push_back(max(v[j-1], v[j])+tmp);
      }
      v = {t.begin(), t.end()}; // 벡터 업데이트
      t.clear();
    }

    cout<<*max_element(v.begin(), v.end())<<endl;
    return 0;
}