[백준/C++]12865번_평범한 배낭

문제는 다음과 같습니다.

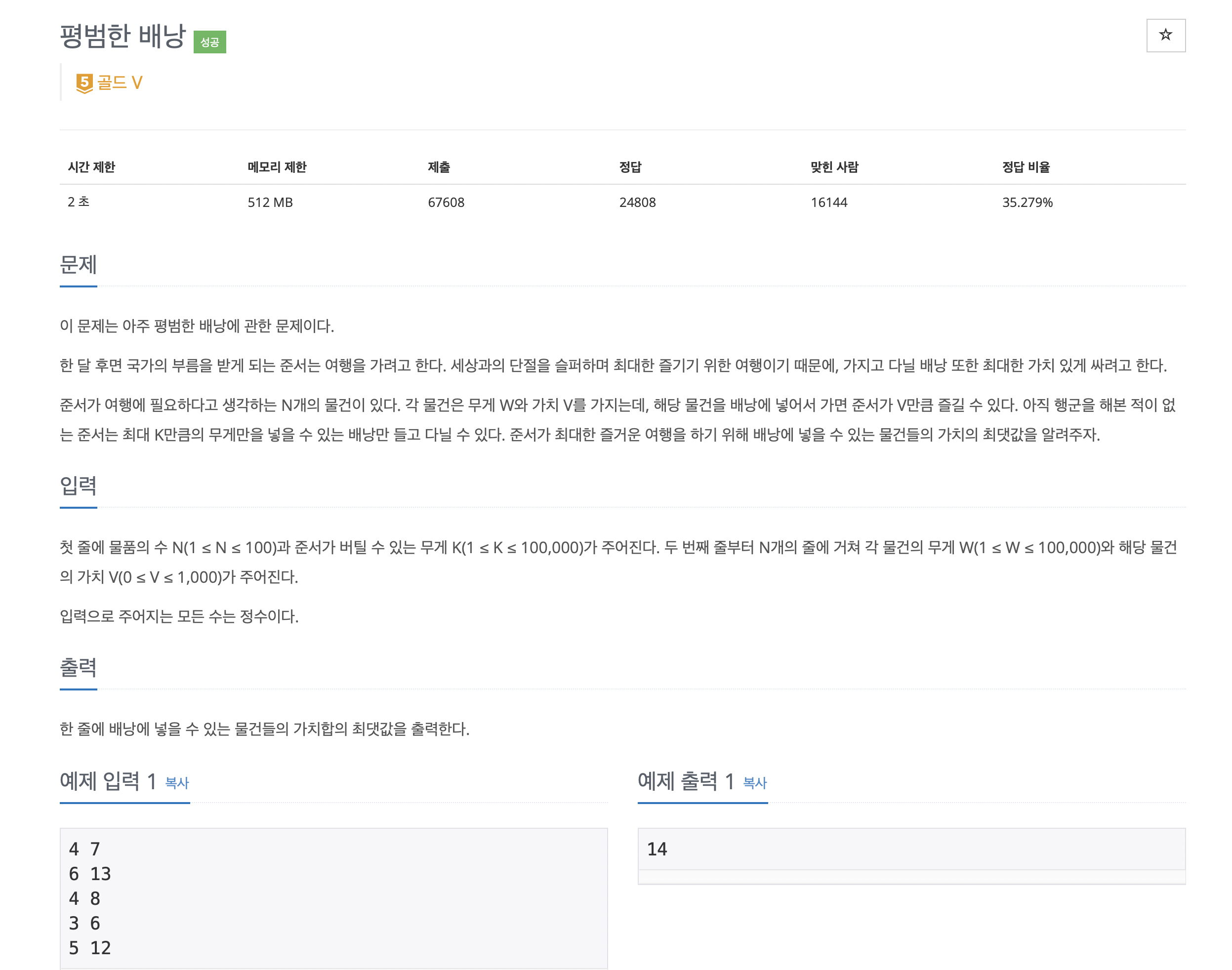
먼저 배낭 문제는 크게 두 개로 나뉩니다.

1. 물건을 쪼갤 수 있는 배낭 문제 -> 그리디 알고리즘

2. 물건을 쪼갤 수 없는 배낭 문제(0-1 배낭) -> 동적 계획법

이 문제는 두 번째에 해당하는 문제입니다.

0-1 배낭 문제를 해결하기 위해서는 동적 계획법을 이용합니다.

2차원 배열 dp에 문제 예시를 직접 진행해보면 다음과 같습니다.

점화식의 규칙은 다음과 같습니다.

먼저 2차원 배열 dp[i][j]는,
i번째 입력값일 때에 무게 j까지 담을 수 있을 때에 최대 가치입니다.

i를 1부터 입력받은 개수 n까지 돌고,
j는 무게이므로, 1부터 담을 수 있는 최대 무게 k만큼 돕니다.

이때에 dp[i][j]는 다음과 같습니다.

if(weight[i] <= j) dp[i][j] = max(value[i] + dp[i-1][j-weight[i]], dp[i-1][j]);

즉, i번째를 포함할 수 있을 때에는
i번째를 포함했을 때 얻을 수 있는 가치와, 포함하지 않았을 때 둘 중 더 큰 가치를 dp에 저장합니다.

else dp[i][j] = dp[i-1][j];

i번째를 포함할 수 없을 때에는,
i-1번째의 그 무게에 값을 dp에 저장합니다.

전체 코드는 다음과 같습니다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int dp[101][100001]={0, };
int weight[101]={0,}; int value[101]={0,};

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, k, w, v;
    cin>>n>>k; // n: 물품의 수, k: 버틸 수 있는 무게

    for(int i=1; i<=n; i++){
        cin>>w>>v; // 무게, 가치 입력받기
        weight[i]=w; value[i]=v;
    }

    for(int i=1; i<=n; i++){
        for(int j=1; j<=k; j++){
            if(weight[i]<=j) dp[i][j] = max(value[i]+dp[i-1][j-weight[i]], dp[i-1][j]);
            else dp[i][j] = dp[i-1][j];
        }
    }

    cout<<dp[n][k]<<endl;
    return 0;
}