[백준/C++]2579번_계단 오르기

문제는 다음과 같습니다.

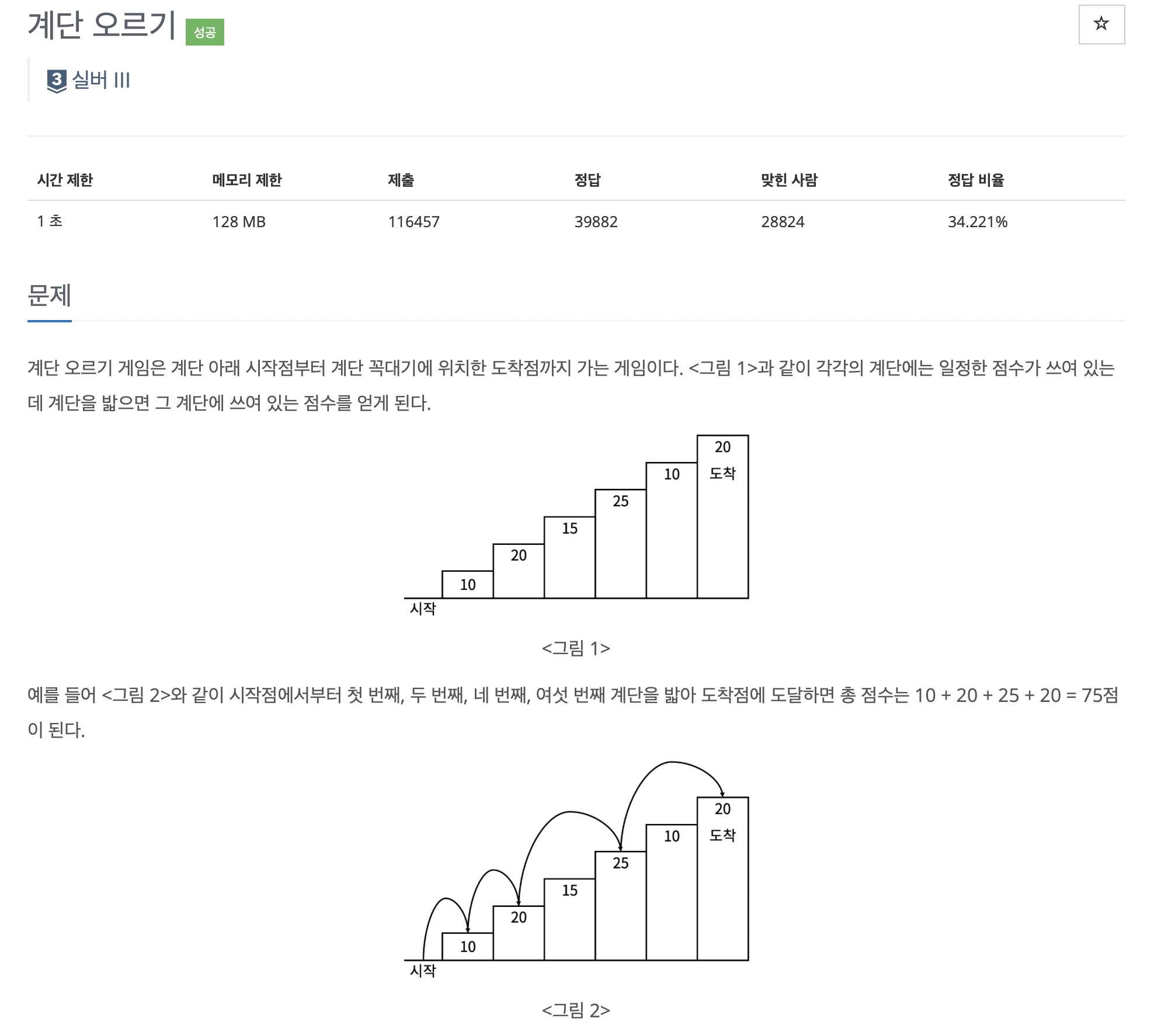
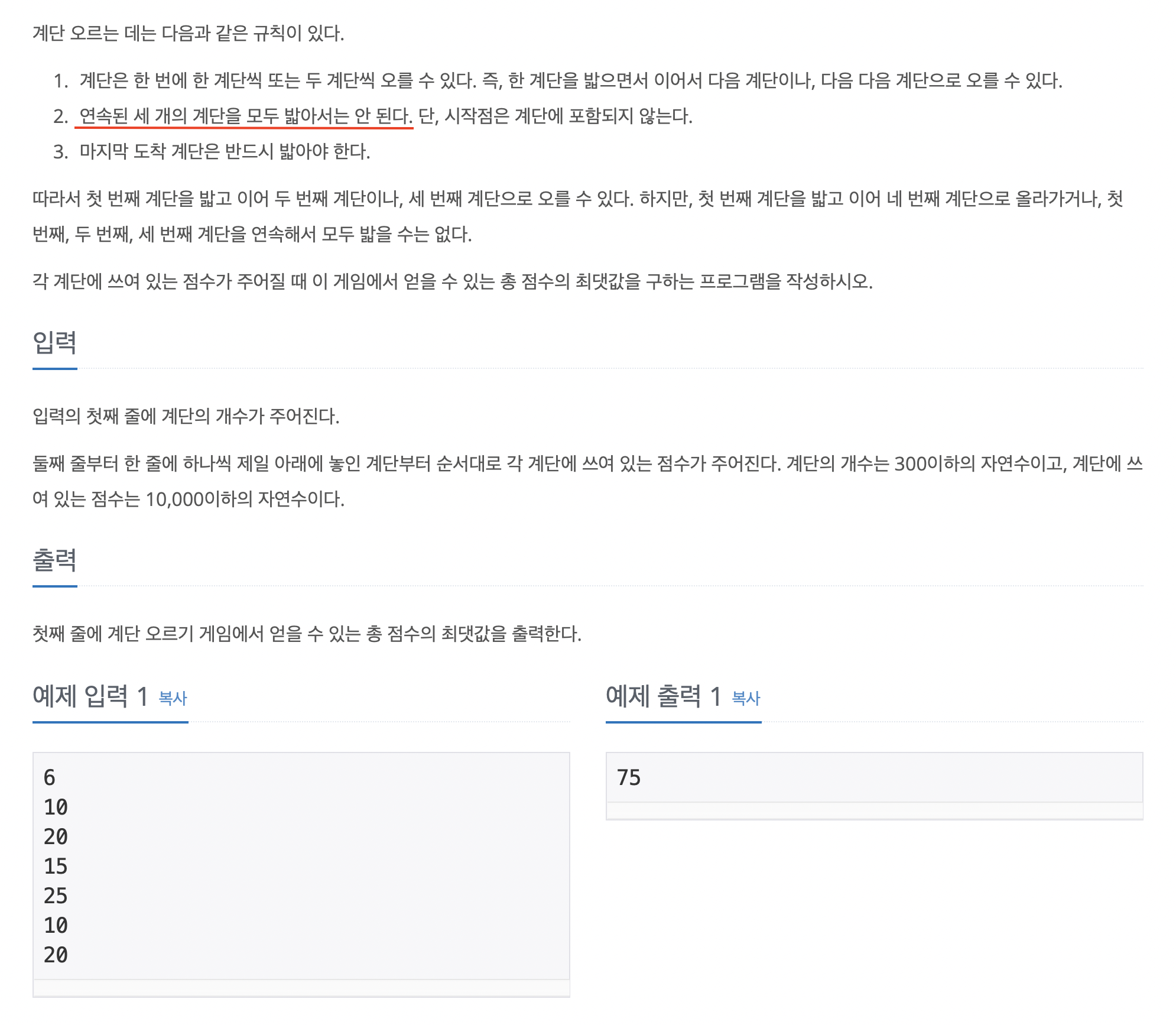
그나마 좀 생각해 볼 만한 지점이 있었던 DP문제입니다.
저기 밑줄 친 "연속된 세 개의 계단을 모두 밟아서는 안된다" 조건이 재밌는 것 같습니다.

먼저 배열 두개가 필요합니다.

• 배열 a는 계단의 점수를 입력받습니다.
• 배열 dp는 정답을 구하기 위한 배열로, 계단 N개를 오르는 데 얻을 수 있는 점수의 최댓값을 저장합니다.

n번째 상황에 대해서 생각해보면
먼저 a[n]을 포함해야 하고,
다음과 같이 두 가지 상황이 있습니다.

• 바로 이 전 계단이 a[n-1]인 경우
• 바로 이 전 계단이 a[n-2]인 경우

첫 번째 상황은
a[n], a[n-1]인 계단을 밟은 상황으로,
계단 a[n-2]는 밟아서는 안됩니다.
따라서 이 경우는 : a[n] + a[n-1] + dp[n-3]로 나타낼 수 있습니다.

두 번째 상황은
a[n], a[n-2]인 계단을 밟은 상황으로,
연속 세 칸에 대해서 고려해 줄 필요가 없습니다.
따라서 이 경우는 : a[n] + dp[n-2]

✅이 두 가지 경우에 대한 최댓값이 dp[n]의 값이 됩니다.

a[n]이 중복되므로 a[n]을 앞으로 빼서 dp[n]을 나타내 보면,

dp[n] = a[n] + max(a[n-1]+dp[n-3], dp[n-2])

가 됩니다

제가 풀었던 풀이과정입니다.

전체 코드는 다음과 같습니다🙆🏻‍♀️

#include <iostream>
#include <vector>
using namespace std;

int main(){
  ios_base::sync_with_stdio(false);
  cin.tie(nullptr);
  cout.tie(nullptr);

  long long dp[301]; int a[301]; int n;

  cin>>n;
  for(int i=0; i<n; i++) cin>>a[i+1]; // 계단 idx: 1부터 시작
  
  dp[1]=a[1], dp[2]=a[1]+a[2]; dp[3]=a[3]+max(a[1], a[2]);// 초기 조건 세팅
  for(int i=4; i<=n; i++){ // bottom-up
      dp[i] = a[i] + max(a[i-1]+dp[i-3], dp[i-2]);
  }

  cout<<dp[n]<<"\n";
  return 0;
}