
세그먼트 트리 (Segment Tree)
개념
- 구간 쿼리, 구간 업데이트에 매우 효율적인 자료구조
- 구간합, 최솟값, 최댓값, 구간 업데이트 등을 O(log N)에 처리하는 트리 구조
- O(N log N)에 트리를 만들고 O(log N)에 쿼리 처리
특징
- 트리 구조: 이진 트리 형태로 구성되며, 트리의 각 노드는 배열의 특정 구간을 나타냄
- 구간 분할: 각 노드는 배열의 일정 부분에 대해 값을 저장하고, 부모 노드는 자식 노드의 값을 결합하여 구간을 대표하는 값을 저장함
- O(log N): 구간 합, 최솟값, 최댓값 구하는 쿼리와 구간 업데이트 연산이 O(log N)의 시간 복잡도를 가짐. 이 때문에 큰 입력에서도 효율적으로 동작
구성
- 트리 노드: 트리의 각 노드는 배열의 구간에 대한 정보를 담고 있다. 예를 들어, 구간 [l, r] 에 대한 값을 나타내는 노드는 배열의 그 구간에 대한 결과값을 저장한다.
- 트리의 깊이: 트리의 깊이는 O(log N)이다. 즉, 트리의 높이는 배열의 크기 N에 비례하며, 각 레벨에서 배열을 반으로 나누면서 분할한다.
- 트리 크기: 트리의 크기는 대체로 4 * N 이 될 수 있다. (배열 크기 N에 대해 트리 노드가 많아질 수 있기 때문)
구현 방식
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이라고 한다.
아래에서 말하는 범위는 모두 arr의 인덱스를 말함.
tree는 인덱스 1부터 시작하게 만든다. → 1부터 시작해서 2 곱하면 왼쪽 자식, 2곱하고 +1 하면 오른쪽 자식 노드를 가리키기 때문에 구현에 용이
- 트리 빌드 → O(N log N)
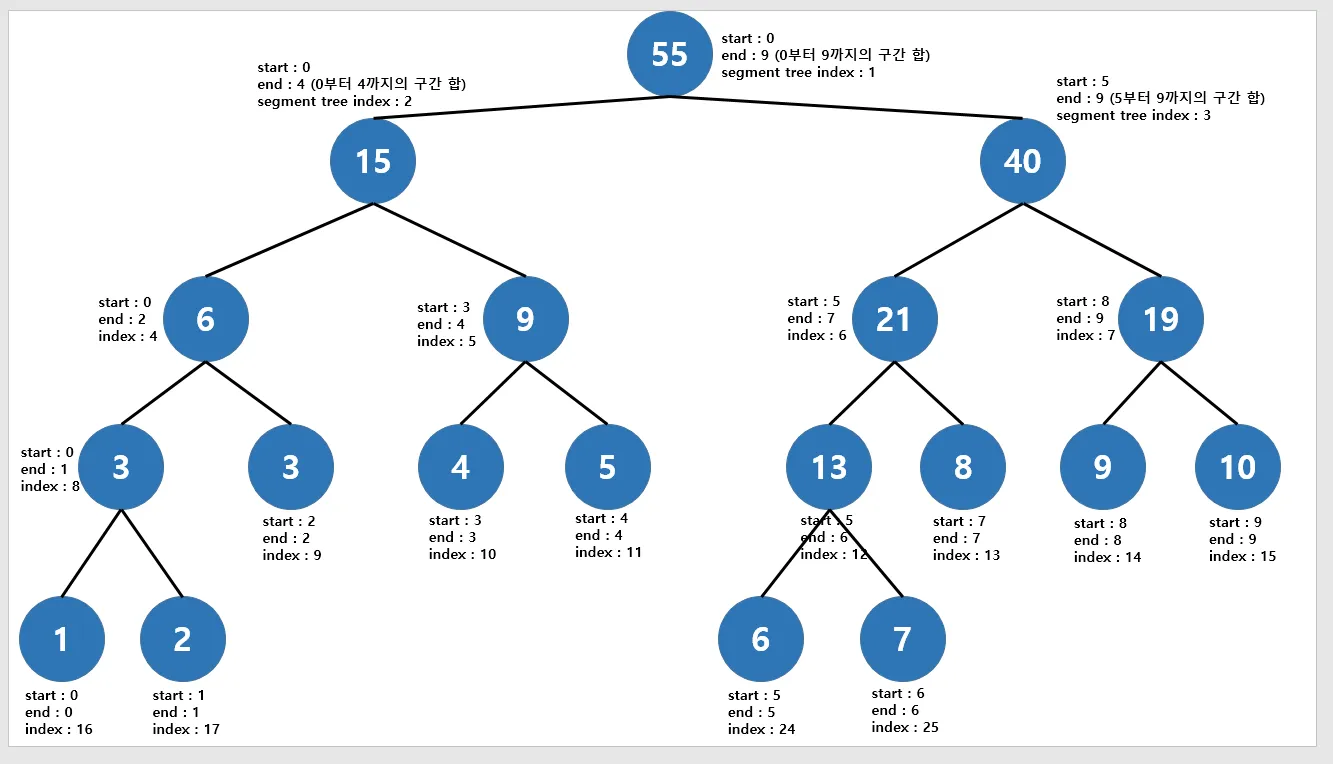
루트 노드부터 보자면, 세그먼트 트리의 루트 노드에는 0~9(인덱스) 까지의 구간합이 삽입되고, 루트 노드의 번호는 1번이다.
루트 노드의 자식 노드
- 왼쪽: 번호는 2, 0~4 까지의 구간합
- 오른쪽: 번호는 3, 5~9 까지의 구간합
# <세그먼트 트리를 배열의 각 구간 합으로 채워주기>
# start : 배열의 시작 인덱스, end : 배열의 마지막 인덱스
# index : 세그먼트 트리의 인덱스 (무조건 1부터 시작)
def init(start, end, index):
# 가장 끝에 도달했으면 arr 삽입
if start == end:
tree[index] = arr[start]
return tree[index]
mid = (start + end) // 2
# 좌측 노드와 우측 노드를 채워주면서 부모 노드의 값도 채워준다.
tree[index] = init(start, mid, index * 2) + init(mid + 1, end, index * 2 + 1)
return tree[index]- 구간합 쿼리 → O(log N)
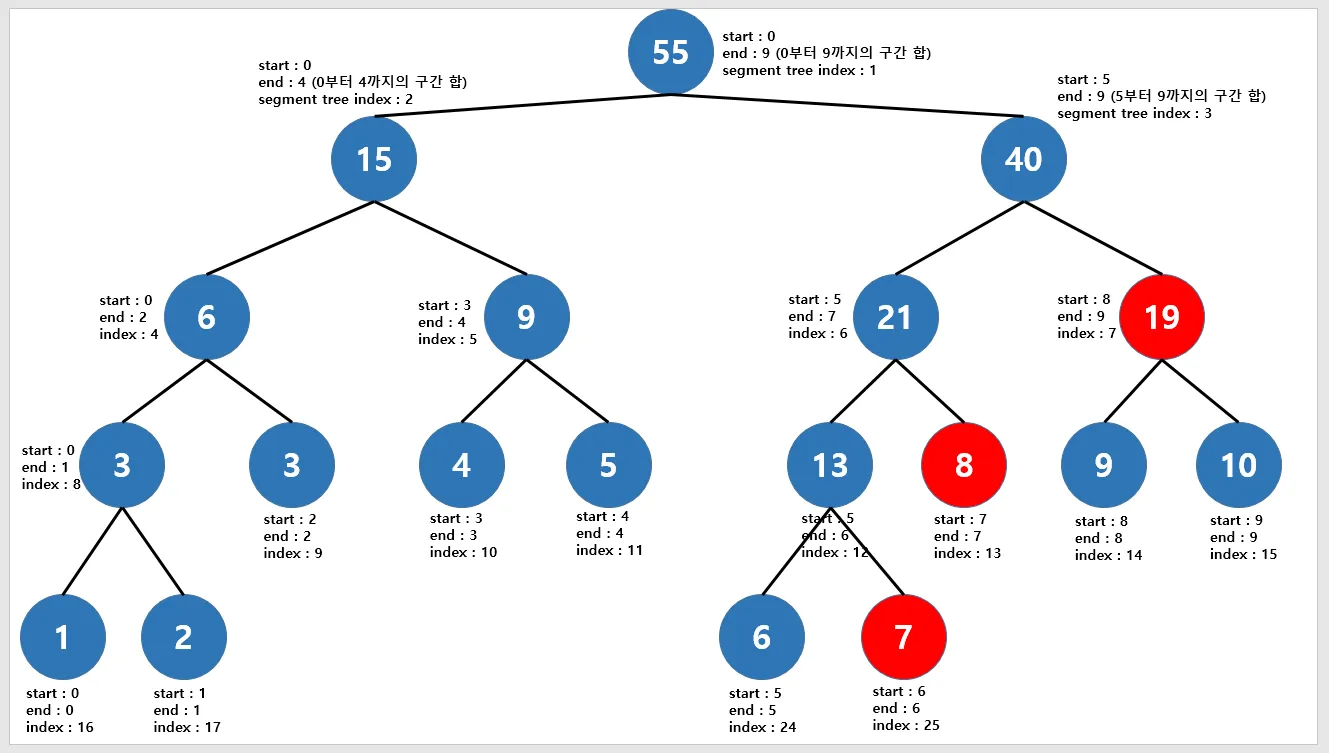
6~9 범위의 구간합을 구할 때, 위 그림처럼 3개의 빨간색 노드의 합을 구하면 된다.
구하고자 하는 6~9 범위의 구간합은 7 + 8 + 9 + 10 = 34이다. 각각 세그먼트 트리 인덱스 7의 값은 19, 인덱스 13의 값은 8, 인덱스 25의 값은 7이다.
즉 19 _ 8 + 7 = 34이다.
구간의 합을 구하는 함수는 재귀적으로 구현. 구간합은 범위 안에 있는 경우에 한해서만 더해주면 됨
직접 해보기: arr = [1, 2, 3, 4, 5] 이고 2~4 구간합 구할 때, 조건을 만족하는 두 노드의 값 더함

# <구간 합을 구하는 함수>
# start : 시작 인덱스, end : 마지막 인덱스
# left, right : 구간 합을 구하고자 하는 범위
def interval_sum(start, end, index, left, right):
# 범위 밖에 있는 경우
if left > end or right < start:
return 0
# 범위 안에 있는 경우
if left <= start and right >= end:
return tree[index]
# 그렇지 않다면 두 부분으로 나누어 합을 구하기
mid = (start + end) // 2
# start와 end가 변하면서 구간 합인 부분을 더해준다고 생각하면 된다.
return interval_sum(start, mid, index * 2, left, right) + interval_sum(mid + 1, end, index * 2 + 1, left, right)- 업데이트 → O(log N)
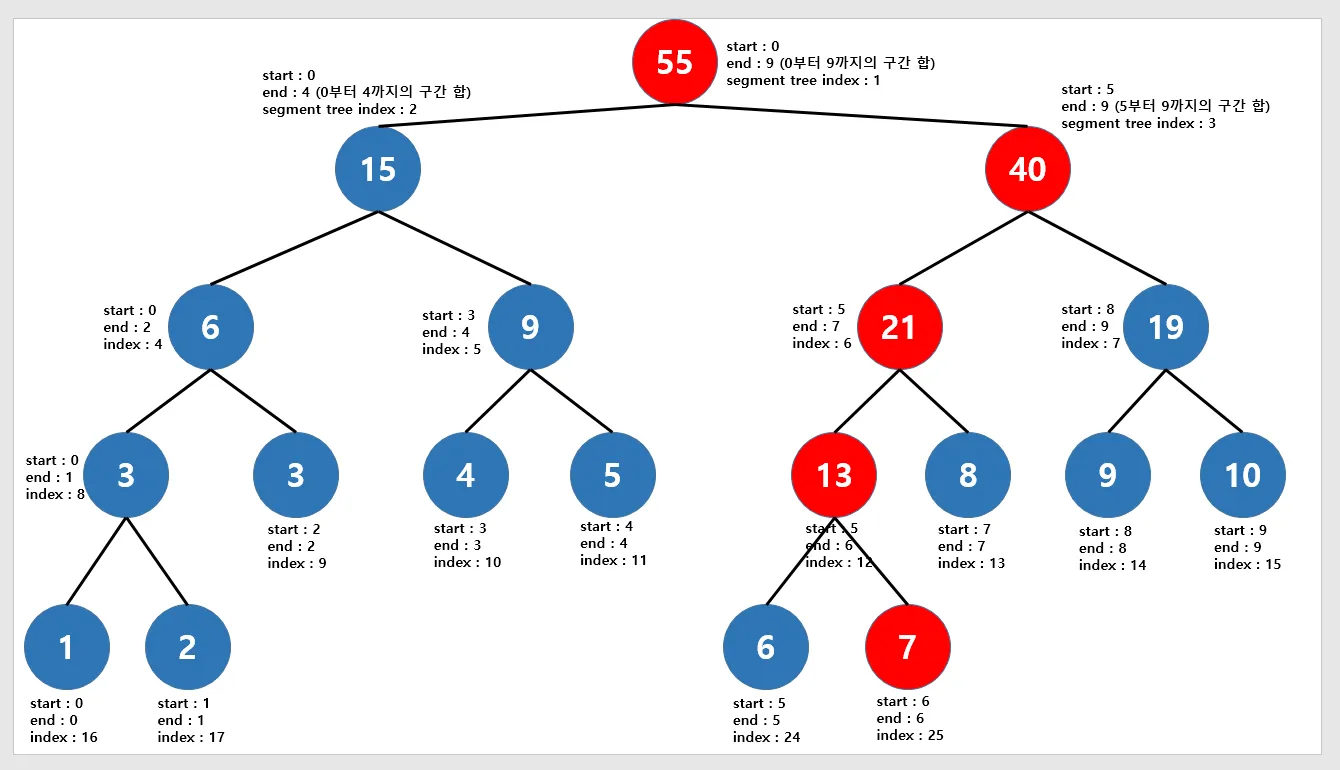
특정 원소를 수정하면 구간의 합들이 달라지고, 세그먼트 트리의 원소값들도 달라진다. 따라서 특정 원소의 값을 수정할 때는 해당 원소를 포함하고 있는 모든 구간 합 노드들을 갱신한다. 이는 모든 노드를 변경하는 것이 아닌 해당 원소를 포함하고 있는 부분적인 노드들만 바꾸는 것을 의미한다.
예를 들어 인덱스 6의 arr[6] 값을 수정할 때, 위와 같이 5개의 구간합 노드를 수정한다.
직접 해보기: arr = [1, 2, 3, 4, 5] 이고 arr[2]를 5로 수정할 때, 아래와 같이 3개의 노드에 값 수정해야함

# <특정 원소의 값을 수정하는 함수>
# start : 시작 인덱스, end : 마지막 인덱스
# what : 구간 합을 수정하고자 하는 노드
# value : 수정할 값
def update(start, end, index, what, value):
# 범위 밖에 있는 경우
if what < start or what > end:
return
# 범위 안에 있으면 내려가면서 다른 원소도 갱신
tree[index] += value
if start == end:
return
mid = (start + end) // 2
update(start, mid, index * 2, what, value)
update(mid + 1, end, index * 2 + 1, what, value)전체 코드
# (Ex)
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# 실제로는 데이터의 개수 N에 4를 곱한 크기만큼 미리 세그먼트 트리의 공간을 할당한다.
tree = [0] * (len(arr) * 4)
# <세그먼트 트리를 배열의 각 구간 합으로 채워주기>
# start : 배열의 시작 인덱스, end : 배열의 마지막 인덱스
# index : 세그먼트 트리의 인덱스 (무조건 1부터 시작)
# 세그먼트 트리가 1부터 시작하는 이유는 2를 곱했을 때 왼쪽 자식노드를 가리키고
# 2를 곱하고 1을 더하면 오른쪽 자식노드를 가리키므로 효과적이기 때문에 이렇게 한다!
def init(start, end, index):
# 가장 끝에 도달했으면 arr 삽입
if start == end:
tree[index] = arr[start]
return tree[index]
mid = (start + end) // 2
# 좌측 노드와 우측 노드를 채워주면서 부모 노드의 값도 채워준다.
tree[index] = init(start, mid, index * 2) + init(mid + 1, end, index * 2 + 1)
return tree[index]
# <구간 합을 구하는 함수>
# start : 시작 인덱스, end : 마지막 인덱스
# left, right : 구간 합을 구하고자 하는 범위
def interval_sum(start, end, index, left, right):
# 범위 밖에 있는 경우
if left > end or right < start:
return 0
# 범위 안에 있는 경우
if left <= start and right >= end:
return tree[index]
# 그렇지 않다면 두 부분으로 나누어 합을 구하기
mid = (start + end) // 2
# start와 end가 변하면서 구간 합인 부분을 더해준다고 생각하면 된다.
return interval_sum(start, mid, index * 2, left, right) + interval_sum(mid + 1, end, index * 2 + 1, left, right)
# <특정 원소의 값을 수정하는 함수>
# 특정 원소를 수정하면 구간 합이 당연히 달라진다.
# 이때, 해당 원소를 포함하고 있는 모든 구간 합 노드들을 갱신해주면 된다.
# (즉, 전체가 아닌 부분적인 노드들만 바꿔주면 된다!)
# start : 시작 인덱스, end : 마지막 인덱스
# what : 구간 합을 수정하고자 하는 노드
# value : 수정할 값의 변경값 (3을 5로 수정하려면 value는 2)
def update(start, end, index, what, value):
# 범위 밖에 있는 경우
if what < start or what > end:
return
# 범위 안에 있으면 내려가면서 다른 원소도 갱신
tree[index] += value
if start == end:
return
mid = (start + end) // 2
update(start, mid, index * 2, what, value)
update(mid + 1, end, index * 2 + 1, what, value)
init(0, len(arr) - 1, 1)
print(interval_sum(0, len(arr) - 1, 1, 0, 9)) # 0부터 9까지의 구간 합 (1 + 2 + ... + 9 + 10)
print(interval_sum(0, len(arr) - 1, 1, 0, 2)) # 0부터 2까지의 구간 합 (1 + 2 + 3)
print(interval_sum(0, len(arr) - 1, 1, 6, 7)) # 6부터 7까지의 구간 합 (7 + 8)
# arr[0]을 +4만큼 수정
update(0, len(arr) - 1, 1, 0, 4)
print(interval_sum(0, len(arr) - 1, 1, 0, 2)) # 0부터 2까지의 구간 합 ((1 + 4) + 2 + 3)
# arr[9]를 -11만큼 수정
update(0, len(arr) - 1, 1, 9, -11)
print(interval_sum(0, len(arr) - 1, 1, 8, 9)) # 8부터 9까지의 구간 합 (9 + (10 - 11))세그먼트 트리 참고: https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%84%B8%EA%B7%B8%EB%A8%BC%ED%8A%B8-%ED%8A%B8%EB%A6%AC-Segment-Tree, https://yoongrammer.tistory.com/103
