Algorithm

📚 문제 설명 🤔 생각한 알고리즘 🖥️ 코드

사야하는 물건의 개수만큼의 배열을 확인해서 배열에 있는 모든 제품의 개수의 합이 더 크다면 answer에 +1을 한다.반복문을 돌려야하는 횟수는 discount 배열의 길이 - 원하는 제품의 총 개수(number의 합) + 1이다.해당하는 길이 i:sum(number)

문제 링크 딕셔너리를 이용해 기록이 IN인 차량을 parking 에 차량 번호를 key, 들어간 시간을 value로 저장한다.OUT이라면 총 시간을 저장하는 딕셔너리인 total_time 에 마찬가지로 차량 번호를 key, 주차되어 있던 시간을 출차시간 - 입차시간을

문제 링크 최단거리를 구하는 문제이기 때문에 알고리즘은 BFS를 이용해 푸는 것이 좋을 것이라 생각을 하였다.상하좌우를 확인할 수 있게 배열을 dx, dy 두 개로 나누어 만들고 시작위치(0,0)부터 탐색하게 하였다.맵을 나가지 않으면서 벽(0)에 막히지 않으면서 1인

문제 링크 처음 문제를 보았을 때는 bruteforce 방식으로 모든 배열을 자를 수 있는 경우의 수를 배열 슬라이싱을 통해 나눠 set 형태로 중복을 없애고 길이를 구해 같은 수의 토핑 종류를 먹도를 할 수 있다고 생각해 코드를 구현하였다.당연하게도 위 코드는 시간

최악의 경우의 시간 복잡도를 우선적으로 고려해야 한다.C언어 기준 연산 횟수 10억에 1초 이상일반적으로 파이썬 프로그램에서는 2,000만 번~1억 번의 연산을 1초의 수행 시간으로 예측됨 (최악의 상황, 보통 2000만번을 1초로 가정)→ C언어가 코테에서 시간복잡도

그리디 특징 현재 상황에서 지금 당장 좋은 것만 고르는 방법 > 💡기준에 따라 좋은 것을 선택하는 알고리즘이기 때문에 문제에서 ‘가장 큰 순서대로’, ‘가장 작은 순서대로’와 같은 기준을 알게 모르게 제시 해준다. 대체로 이 기준은 정렬 알고리즘을 사용했을 때

최근에 알고리즘 문제를 풀 때 프로그래머스로만 풀었더니 입출력 하는게 너무 귀찮아서 정리해보았다.input() : 한줄을 읽어옴int() : 정수로 변환input().split(구분 문자) : 한줄을 읽고 구분 문자로 나눠서 문자로 이뤄진 리스트로 입력 받는다.map(

머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정 → 소위 피지컬이라고도 한다.사소한 조건 설정이 많은 문제일수록 코드로 구현하기 까다롭다.이 책에서는 완전 탐색, 시뮬레이션 유형을 구현 유형으로 묶어 다룬다.완전 탐색 - 모든 경우의 수를 주저 없이 다 계산하는 해결

DFS는 최대한 깊이 들어간 후 더 이상 갈 곳이 없으면 되돌아오는 방식으로 탐색하는 알고리즘이다.보통 재귀 함수 또는 스택을 사용해서 구현한다.시작 노드에서 출발하여 한 방향으로 최대한 이동한다.더 이상 갈 곳이 없으면 이전 노드로 돌아가 다른 경로를 탐색한다.모든

트리가 주어지는데 루트가 없는 상태다.루트를 1번 노드로 정한다.각 노드의 부모를 찾아야 한다.N-1개의 간선이 주어지므로, 트리의 기본 성질(노드 N개 → 간선 N-1개)이 성립함.출력은 2번 노드부터 차례대로 부모 노드를 출력해야 한다.그래프 표현 방법인접 리스트

배열의 앞에서부터 특정 인덱스까지의 합을 미리 계산해두는 기법빠르게 구간합을 구할 수 있음일반적으로 prefix\[i] = prefix\[i-1] + arr\[i] 형태로 계산특정 구간 \[L, R] 의 합을 구하는 문제누적합을 사용하면 prefix\[R] - pref

구간 쿼리, 구간 업데이트에 매우 효율적인 자료구조구간합, 최솟값, 최댓값, 구간 업데이트 등을 O(log N)에 처리하는 트리 구조O(N log N)에 트리를 만들고 O(log N)에 쿼리 처리트리 구조: 이진 트리 형태로 구성되며, 트리의 각 노드는 배열의 특정 구

재귀호출 관련(백트래킹, DFS) PS에 특히 약하기 때문에 재귀호출을 제대로 공부해보려 한다.예: 팩토리얼(Factorial), 피보나치 수열(Fibonacci Sequence)특징: 문제를 작은 단위로 쪼개서 반복적으로 호출하며 해결. 종료 조건(Base Case)

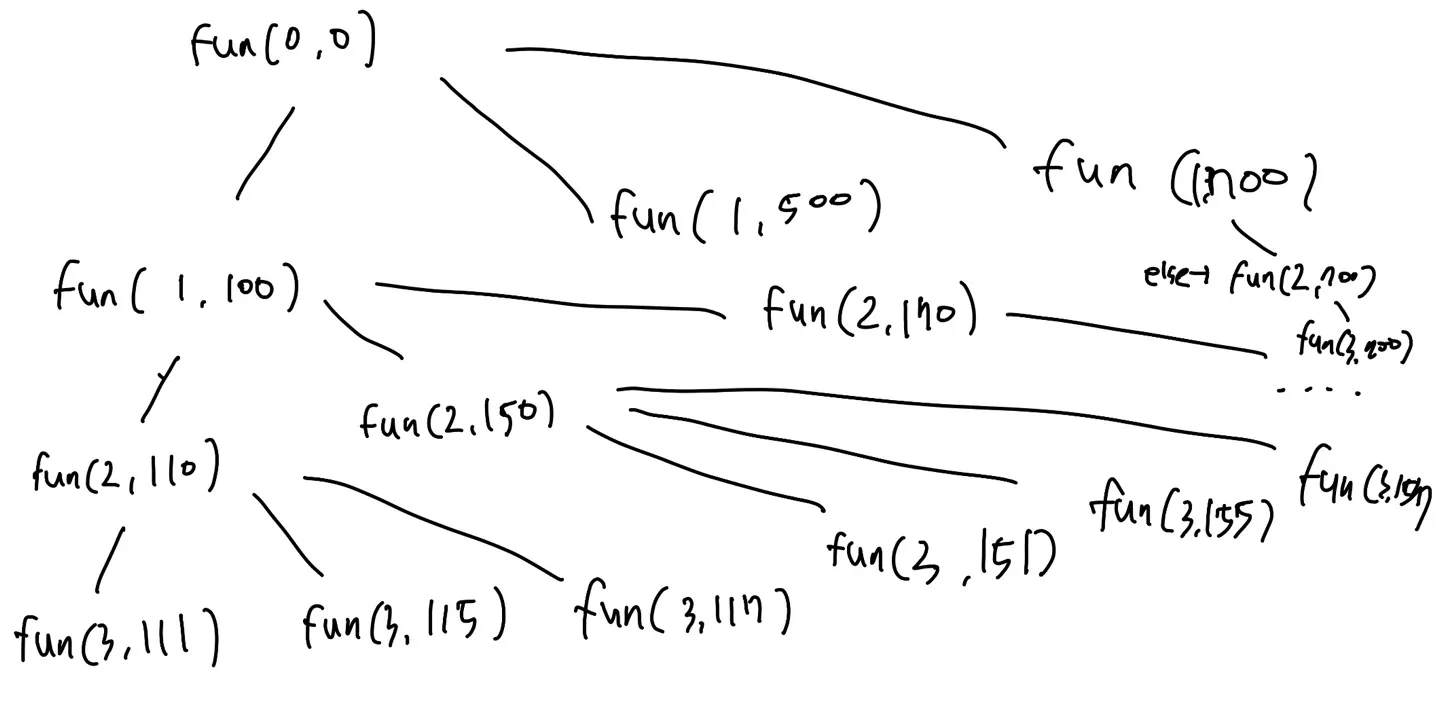
depth는 길이, → 종료 조건은 깊이, 정답에는 비교 후 큰 것 넣도록집합에 있는 자연수는 1~9의 자연수, 이 자연수는 중복해서 사용할 수 있다.N의 자릿수를 넘어가면 어차피 N보다 커지기 때문에 구할 필요가 없음, 따라서 함수의 반환(종료) 조건은 자릿수가 N과