n213_Ridge Regression

ssu_hyun·2021년 8월 22일
AI Bootcamp
0

[codestates] AI Bootcamp

목록 보기
15/62

학습 목표

  • 범주형(Cagegorical) 자료를 다루기 위한 원핫인코딩(One-hot encoding) 기법을 이해합니다.
  • Ridge 회귀를 통한 특성선택(Feature selection) 과정을 이해합니다.
  • 정규화(regularization)을 위한 Ridge 회귀모델을 이해하고 사용할 수 있습니다.


판다스 프로파일링(Pandas-Profiling)

좋은 머신 러닝 결과를 얻기 위해서는 데이터의 성격을 파악하는 과정이 선행되어야 합니다. 이 과정에서 데이터 내 값의 분포, 변수 간의 관계, Null 값과 같은 결측값(missing values) 존재 유무 등을 파악하게 되는데 이와 같이 데이터를 파악하는 과정을 EDA(Exploratory Data Analysis, 탐색적 데이터 분석)이라고 합니다.

판다스 프로파일링(Pandas-Profiling)은 방대한 양의 데이터를 가진 데이터프레임을 .profile_report()라는 단 한 줄의 명령으로 탐색하는 패키지입니다.

#패키지 설치
!pip install pandas-profiling[notebook]

#패키지 설치2 : 코드실행-런타임 다시시작-다시실행
import sys
!{sys.executable} -m pip install -U pandas-profiling[notebook]
!jupyter nbextension enable --py widgetsnbextension


#패키지 설치3 : 삭제 후 다시 설치
!pip uninstall pandas-profiling
!pip install pandas-profiling[notebook,html]

## panas profiling이 실행되지 않을 시 설치/업그레이드 진행
!pip install pandas-profiling==2.11.0 --upgrade


import pandas as pd
import pandas_profiling
data = pd.read_csv('spam.csv 파일의 경로',encoding='latin1')

pr=data.profile_report() # 프로파일링 결과 리포트를 pr에 저장
data.profile_report() # 바로 결과 보기


원핫인코딩(One-hot encoding)

scikit-learn에서 제공하는 머신러닝 알고리즘은 문자열 값을 입력 값으로 허락하지 않기 때문에 모든 문자열 값들을 숫자형으로 인코딩하는 전처리 작업(Preprocessing) 후에 머신러닝 모델에 학습을 시켜야 합니다.

※ scikit-learn 에서 제공하는 머신러닝 알고리즘에 데이터를 넣을 수 있는 기본 조건

  • 모든 데이터는 숫자(정수형, 실수형 등)로 구성되어 있어야 한다.
  • 데이터에 빈 값이 없어야 한다.


원핫인코딩은 각 범주형 변수를 0 또는 1 값을 가진 하나 이상의 새로운 특성으로 바꾼 것으로 단어 집합의 크기(Cardinality, 범주형 변수 값의 종류)를 벡터의 차원으로 하고, 표현하고 싶은 단어의 인덱스에 1의 값을 부여하고, 다른 인덱스에는 0을 부여하는(정수 인코딩) 단어의 벡터 표현 방식입니다. 이렇게 표현된 벡터를 원-핫 벡터(One-Hot vector)라고 합니다.

분류문제에서는 n개의 카테고리 값이 존재할 때 n개 카테고리 모두 인코딩을 하지만 회귀문제에서는 자유도(degree of freedom)를 반영하므로 n-1개의 카테고리값들을 인코딩해줍니다.


※ 한계

  • 단어의 개수가 늘어날 수록, 벡터를 저장하기 위해 필요한 공간이 계속 늘어난다.(벡터의 차원이 계속 늘어난다.) → 카테고리가 너무 많은 경우(high cardinality)에는 사용하기 적합하지 않다.
    -단어의 유사도를 표현하지 못한다. 극단적으로는 강아지, 개, 냉장고라는 단어가 있을 때 강아지라는 단어가 개와 냉장고라는 단어 중 어떤 단어와 더 유사한지도 알 수 없습니다. (모두 수치화되면 알 수 없으므로) → 검색 시스템 등에서 심각한 문제

Pandas_get_dummies

1. df 전체
pd.get_dummies(fruit)

2. df에서 특정 열 인코딩
pd.get_dummies(fruit, columns = ['name'])  #기존 df에 인코딩 컬럼 반영
pd.get_dummies(fruit, prefix=['name'])  #새로운 df 생성

3. 회귀문제_열을 n-1개 생성(feat.자유도)
pd.get_dummies(fruit['name'], drop_first=True)   #N-1개 생성

4. 결측값 처리
pd.get_dummies(fruit['name'], dummy_na = True)

Category_encoders_OneHotEncoder

!pip install category_encoders

features = ['City','Room']
target = 'Price'

# 이번에는 훈련/테스트 데이터를 분리해 만들어 보겠습니다.
X_train = df[features][:8]
y_train = df[target][:8]
X_test = df[features][8:]
y_test = df[target][8:]

# import OneHotEncoder
from category_encoders import OneHotEncoder

# 원핫 인코딩
encoder = OneHotEncoder(use_cat_names = True)
X_train = encoder.fit_transform(X_train)
X_test = encoder.transform(X_test)

❓transform() vs fit_transform()

fit()

  • 학습 데이터 세트에서 변환을 위한 기반(예를 들어 학습 데이터 세트의 최대값/최소값등)을 설정하고 그 값을 StandardScaler와 같은 메서드 내부에 저장하는 단계
  • 만약 fit()을 test data에도 적용해 데이터를 변환시켜버리면 기존의 훈련 데이터에서 저장했던 내부의 값들, 기준들을 모두 무시하고 새로운 값들을 저장하여 적용하게되므로 test data의 경우 train data에 적용한 값들을 기반으로 transform()메서드만 사용해 변환시켜야 하는 것(학습할 때와 동일한 기반 설정으로 동일하게 테스트 데이터를 변환해야 하는 것)

transform()

  • fit메서드에서 저장한 설정값들을 기반으로 데이터를 변환하는 메서드

fit_transform()



특성 선택(Feature selection)


특성공학(feature engineering)

: 특성공학은 과제에 적합한 특성을 만들어 내는 과정으로 실무 현장에서 가장 많은 시간이 소요되는 작업 중 하나입니다.

특성 선택 시 주의할 점

타겟 특성과 이름은 다르지만 내용은 거의 동일하다고 볼 수 있는 독립변수 특성(ex. 타겟 - '결제금액', 독립변수 특성 - '주문금액' )이 있을 경우, 결제금액과 주문금액이 데이터가 만들어 지는 과정에서 실수로 학습 특성에 사용하는 경우가 있을 수 있습니다. 실제 타겟과 거의 유사한 데이터인 독립변수는 제거하고 사용하지 않으면 모델이 과적합이 일어날 수 있습니다. 이런 경우 동일한 테스트 데이터를 만들 수 없는 경우가 발생합니다. 이러한 문제를 데이터 누수(Data Leakage)문제라고 합니다. 따라서, 특성 선택에서 타겟과 상관성이 높다고 하여 해당 독립변수 특성을 반드시 사용할 수 있는 것은 아니며, 상관성이 너무 높으면 제거해야 할 수도 있음을 기억해두시면 좋습니다.

단일 변수 선택(Univariate feature selection)

단일 변수 선택법은 각각의 독립변수를 하나만 사용한 예측모형의 성능을 이용하여 가장 분류성능 혹은 상관관계가 높은 변수만 선택하는 방법이다. 사이킷런 패키지의 feature_selection 서브패키지는 다음 성능지표를 제공한다.

  • chi2: 카이제곱 검정 통계값
  • f_classif: 분산분석(ANOVA) F검정 통계값
  • mutual_info_classif: 상호정보량(mutual information)

SelectKBest_score the features

  • removes all but the k highest scoring features
  • target과 가장 correlated 된 features 를 k개 고르는 것이 목표

특성 수 k 결정 방법

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score

training = []
testing = []
ks = range(1, len(X_train.columns)+1)

# 1 부터 특성 수 만큼 사용한 모델을 만들어서 MAE 값을 비교 합니다.
for k in range(1, len(X_train.columns)+ 1):
    print(f'{k} features')
    
    selector = SelectKBest(score_func=f_regression, k=k)
    
    X_train_selected = selector.fit_transform(X_train, y_train)
    X_test_selected = selector.transform(X_test)
    
    all_names = X_train.columns
    selected_mask = selector.get_support()
    selected_names = all_names[selected_mask]
    print('Selected names: ', selected_names)

    
    model = LinearRegression()
    model.fit(X_train_selected, y_train)
    y_pred = model.predict(X_train_selected)
    mae = mean_absolute_error(y_train, y_pred)
    training.append(mae)
    
    y_pred = model.predict(X_test_selected)
    mae = mean_absolute_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)
    testing.append(mae)
    print(f'Test MAE: ${mae:,.0f}')
    print(f'Test R2: {r2} \n')

plt.plot(ks, training, label='Training Score', color='b')
plt.plot(ks, testing, label='Testing Score', color='g')
plt.ylabel("MAE ($)")
plt.xlabel("Number of Features")
plt.title('Validation Curve')
plt.legend()
plt.show()


>>>
1 features
Selected names:  Index(['sqft_living'], dtype='object')
Test MAE: $167,321
Test R2: 0.4296149194220933 

2 features
Selected names:  Index(['sqft_living', 'grade'], dtype='object')
Test MAE: $157,239
Test R2: 0.4884712916259375 

3 features
Selected names:  Index(['sqft_living', 'grade', 'sqft_living15'], dtype='object')
Test MAE: $156,951
Test R2: 0.49204137332086406 

4 features
Selected names:  Index(['sqft_living', 'grade', 'sqft_above', 'sqft_living15'], dtype='object')
Test MAE: $154,920
Test R2: 0.5019286655041768 

5 features
Selected names:  Index(['bathrooms', 'sqft_living', 'grade', 'sqft_above', 'sqft_living15'], dtype='object')
Test MAE: $154,979
Test R2: 0.5020209934516052 

6 features
Selected names:  Index(['bathrooms', 'sqft_living', 'grade', 'sqft_above', 'sqft_living15',
       'rooms'],
      dtype='object')
Test MAE: $154,376
Test R2: 0.505157284321 

7 features
Selected names:  Index(['bathrooms', 'sqft_living', 'view', 'grade', 'sqft_above',
       'sqft_living15', 'rooms'],
      dtype='object')
Test MAE: $149,839
Test R2: 0.5326279698432828 

8 features
Selected names:  Index(['bathrooms', 'sqft_living', 'view', 'grade', 'sqft_above', 'lat',
       'sqft_living15', 'rooms'],
      dtype='object')
Test MAE: $126,250
Test R2: 0.626639246589956 

9 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'view', 'grade', 'sqft_above',
       'lat', 'sqft_living15', 'rooms'],
      dtype='object')
Test MAE: $126,250
Test R2: 0.6266392465899528 

10 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'view', 'grade', 'sqft_above',
       'sqft_basement', 'lat', 'sqft_living15', 'rooms'],
      dtype='object')
Test MAE: $126,250
Test R2: 0.6266392465899531 

11 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'floors', 'view', 'grade',
       'sqft_above', 'sqft_basement', 'lat', 'sqft_living15', 'rooms'],
      dtype='object')
Test MAE: $126,257
Test R2: 0.6273262157764314 

12 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'floors', 'view', 'grade',
       'sqft_above', 'sqft_basement', 'yr_renovated', 'lat', 'sqft_living15',
       'rooms'],
      dtype='object')
Test MAE: $125,795
Test R2: 0.6313843084113078 

13 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'view',
       'grade', 'sqft_above', 'sqft_basement', 'yr_renovated', 'lat',
       'sqft_living15', 'rooms'],
      dtype='object')
Test MAE: $125,916
Test R2: 0.6308283765248046 

14 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'view',
       'grade', 'sqft_above', 'sqft_basement', 'yr_renovated', 'lat',
       'sqft_living15', 'sqft_lot15', 'rooms'],
      dtype='object')
Test MAE: $125,920
Test R2: 0.631430772664115 

15 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'view',
       'grade', 'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated',
       'lat', 'sqft_living15', 'sqft_lot15', 'rooms'],
      dtype='object')
Test MAE: $119,578
Test R2: 0.6677358410398337 

16 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'view',
       'grade', 'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated',
       'zipcode', 'lat', 'sqft_living15', 'sqft_lot15', 'rooms'],
      dtype='object')
Test MAE: $119,295
Test R2: 0.6697817823179242 

17 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'view',
       'condition', 'grade', 'sqft_above', 'sqft_basement', 'yr_built',
       'yr_renovated', 'zipcode', 'lat', 'sqft_living15', 'sqft_lot15',
       'rooms'],
      dtype='object')
Test MAE: $118,769
Test R2: 0.671066324876241 

18 features
Selected names:  Index(['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'view',
       'condition', 'grade', 'sqft_above', 'sqft_basement', 'yr_built',
       'yr_renovated', 'zipcode', 'lat', 'long', 'sqft_living15', 'sqft_lot15',
       'rooms'],
      dtype='object')
Test MAE: $118,992
Test R2: 0.6750956927564506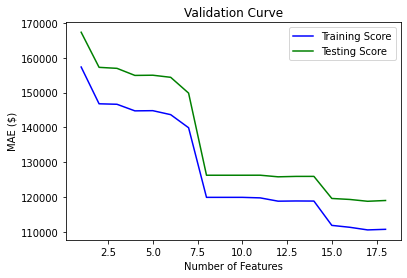

특성 k개 고르기


from sklearn.feature_selection import f_regression, SelectKBest

# selctor 정의
selector = SelectKBest(score_func=f_regression, k=10) 
# f_regression:F-value between label/feature for regression tasks.
# k:Number of top features to select
>>> return a pair of arrays(scores, pvalues)  or  single array with scores

# 학습데이터 => fit_transform(X[, y]):Fit to data, then transform it.
X_train_selected = selector.fit_transform(X_train, y_train)

# 테스트 데이터 => transform(X):Reduce X to the selected features.
X_test_selected = selector.transform(X_test)

X_train_selected.shape, X_test_selected.shape

선택된 특성 확인

# selection된 특성 print
df_scores = pd.DataFrame(selector.scores_)
df_columns = pd.DataFrame(X_train.columns)

feature_scores = pd.concat([df_columns, df_scores], axis=1)
feature_scores.columns = ['Feature_Name', 'Score']

print(feature_scores.nlargest(20,'Score'))

___________________________________________________________

all_names = X_train.columns

## selector.get_support()
selected_mask = selector.get_support()

## 선택된 특성들
selected_names = all_names[selected_mask]

## 선택되지 않은 특성들
unselected_names = all_names[~selected_mask] 

print('Selected names: ', selected_names)
print('Unselected names: ', unselected_names)


릿지 회귀(Ridge Regression)


정규화 선형회귀


정규화(regularized) 선형회귀 방법은 선형회귀 계수(weight)에 대한 제약 조건을 추가함으로써 모형이 과도하게 최적화되는 현상, 즉 과최적화를 막는 방법입니다.

모형이 과도하게 최적화되면 모형 계수의 크기도 과도하게 증가하는 경향이 나타납니다. 따라서 정규화 방법에서 추가하는 제약 조건은 일반적으로 계수의 크기를 제한하는 방법으로, 베타값(파라미터값)에 제약을 줌으로써 모델을 정돈하여 일반성을 띄게 해주는 것입니다.

(1)Training accuray만 있으면 최소제곱법과 다른게 없지만 (2)Generalization accuaracy가 추가되면서 베타에 제약을 줄 수 있어 정규화가 가능해지게 됩니다. 이렇게 계수 추정치를 줄여주는 정규화 방법을 shrinkage method라고 말하기도 합니다.

  • Ridge 회귀모형
  • Lasso 회귀모형
  • Elastic Net 회귀모형

릿지회귀(Ridge Regression, L2 Regression)

일반 선형회귀 모델을 사용하다 보면 과적합이 생길때가 빈번하게 있습니다. 이때, 과적합을 줄이기 위해서 사용하는것이 바로 릿지회귀입니다. 과적합을 줄이는 간단한 방법 중 한 가지는 모델의 복잡도를 줄이는 방법으로 특성의 갯수를 줄이거나 모델을 단순한 모양으로 적합하는 방법이 있습니다.
Ridge 회귀는 편향을 조금 더하고, 분산을 줄이는 방법으로 정규화(Regularization)를 수행합니다. 정규화에서는 보통 같은 수의 변수를 유지하면서 계수 j의 크기를 줄이는 일을 합니다. 즉 모델을 변형하여 과적합을 완화해 일반화 성능을 높여주는 것 입니다. Ridge 회귀는 정규화를 통해 특이값으로 인한 과도한 기울기를 보정해줍니다. 또한 영향력이 낮은 특성의 회귀계수의 값을 감소시켜 특징선택 효과를 가져옵니다.

βridge\beta_{ridge}: argmin[∑i=1n(yi−β0−β1xi1−…−βpxip)2+λ∑j=1pβj2]argmin[\sum_{i=1}^n(y_i - \beta_0 - \beta_1x_{i1}-\dotsc-\beta_px_{ip})^2 + \lambda\sum_{j=1}^p\beta_j^2]

n: 샘플수, p: 특성수, λ\lambda: 튜닝 파라미터(패널티)
참고: alpha, lambda, regularization parameter, penalty term 모두 같은 뜻 입니다.
*잔차제곱합(RSS : residual sum of squares) + 패널티 항(베타 값)의 합
*패널티 항 = 파라미터의 제곱의 합

평균 제곱 오차 식(RSS) + λ∑j=1pβj2\lambda\displaystyle\sum_{j=1}^{p} \beta_j^2
=> λ\lambda값을 크게 하면 패널티의 효과가 커집니다.(가중치 감소)


릿지회귀는 람다(λ)를 통해 편향을 조금 더하고, 분산을 줄이는 방법으로 정규화(Regularization)를 진행합니다. Ridge는 alpha값을 통해 모델을 단순하게 (계수를 0에 가깝게) 해주고 훈련 세트에 대한 성능 사이를 절충할 수 있는 방법을 제공합니다. 사용자는 alpha 매개변수로 훈련 세트의 성능 대비 모델을 얼마나 단순화할지를 지정할 수 있으며 alpha값을 높일수록 강한 규제로 모델의 coef_(계수)의 절댓값 크기가 줄어들게 됩니다.(기울기 감소)

정규화의 강도를 조절해주는 패널티값인 람다는 다음과 같은 성질이 있습니다.

λ\lambda → 0, βridge\beta_{ridge} → βOLS\beta_{OLS}
λ\lambda → ∞, βridge\beta_{ridge} → 0.

alpha = 0인 경우에는 OLS 와 같은 그래프 형태로 같은 모델 임을 확인 할 수 있고. alpha 값이 커질 수록 직선의 기울기가 0에 가까워 지면서 평균 기준모델(baseline) 과 비슷해지는 모습을 볼 수 있습니다.



RidgeCV : 교차 검증이 내장 된 릿지 회귀


교차검증(Cross-validation)을 사용해 훈련/검증 데이터를 나누어 여러 패널티(alpha, lambda) 값을 가지고 검증실험을 진행합니다. 
from sklearn.linear_model import RidgeCV

alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0]

ridge = RidgeCV(alphas=alphas, normalize=True, cv=3)
ridge.fit(ans[['x']], ans['y'])
print("alpha: ", ridge.alpha_)
print("best score: ", ridge.best_score_)
def RidgeCVRegression(degree=3, **kwargs):
    return make_pipeline(PolynomialFeatures(degree), 
                         RidgeCV(**kwargs))

# alphas = np.linspace(0.01, 0.5, num=20)
alphas = np.arange(0.01, 0.2, 0.01)

model = RidgeCVRegression(alphas=alphas, normalize=True, cv=5)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Test MAE: ${mae:,.0f}')
print(f'R2 Score: {r2:,.4f}\n')

coefs = model.named_steps["ridgecv"].coef_
print(f'Number of Features: {len(coefs)}')

print(f'alpha: {model.named_steps["ridgecv"].alpha_}')
print(f'cv best score: {model.named_steps["ridgecv"].best_score_}') # best score: R2


>>>
Test MAE: $111,705
R2 Score: 0.6945

Number of Features: 1330
alpha: 0.06999999999999999
cv best score: 0.7403019606698997

여러 특성을 통한 Ridge 회귀 학습

from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score

for alpha in [0.001, 0.005, 0.01, 0.02, 0.03, 0.1, 1.0, 1, 100.0, 1000.0]:
        
    print(f'Ridge Regression, alpha={alpha}')

    # Ridge 모델 학습
    model = Ridge(alpha=alpha, normalize=True)  
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)

    # MAE for test
    mae = mean_absolute_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)
    
    print(f'Test MAE: ${mae:,.0f}')
    print(f'Test R2: {r2:,.3f}')
    
    # plot coefficients
    coefficients = pd.Series(model.coef_, X_train.columns)
    plt.figure(figsize=(10,3))
    coefficients.sort_values().plot.barh()
    plt.show()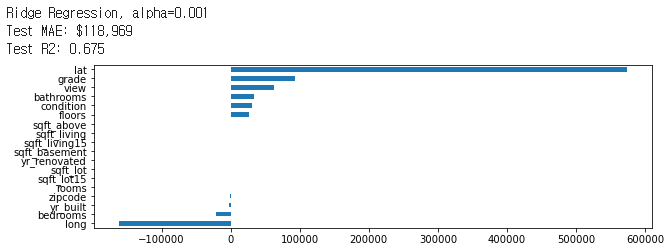



다항함수 Ridge 회귀

다수의 특성을 사용하는 다항함수에 Ridge 회귀를 사용하면 정규화 효과를 더 잘 확인할 수 있습니다.

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

def RidgeRegression(degree=3, **kwargs):
    return make_pipeline(PolynomialFeatures(degree), 
                         Ridge(**kwargs))


for alpha in [0.001, 0.01, 0.0025, 0.05, 0.09, 0.12, 0.4, 1.0, 1, 5, 10, 100]:
        
    print(f'Ridge Regression, alpha={alpha}')

    # Ridge 모델 학습
    model = RidgeRegression(alpha=alpha, normalize=True)
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)

    # MAE for test
    mae = mean_absolute_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)
    print(f'Test MAE: ${mae:,.0f}')
    print(f'R2 Score: {r2:,.4f}\n')

coefs = model.named_steps["ridge"].coef_
print(f'Number of Features: {len(coefs)}')

>>>
Ridge Regression, alpha=0.001
Test MAE: $115,090
R2 Score: -0.5563

Ridge Regression, alpha=0.01
Test MAE: $112,684
R2 Score: 0.5540

Ridge Regression, alpha=0.0025
Test MAE: $113,995
R2 Score: 0.0050

Ridge Regression, alpha=0.05
Test MAE: $111,764
R2 Score: 0.6929

Ridge Regression, alpha=0.09
Test MAE: $111,875
R2 Score: 0.6943

Ridge Regression, alpha=0.12
Test MAE: $112,023
R2 Score: 0.6936

Ridge Regression, alpha=0.4
Test MAE: $112,310
R2 Score: 0.6928

Ridge Regression, alpha=1.0
Test MAE: $112,566
R2 Score: 0.6914

Ridge Regression, alpha=1
Test MAE: $112,566
R2 Score: 0.6914

Ridge Regression, alpha=5
Test MAE: $116,650
R2 Score: 0.6680

Ridge Regression, alpha=10
Test MAE: $121,811
R2 Score: 0.6442

Ridge Regression, alpha=100
Test MAE: $150,360
R2 Score: 0.5087

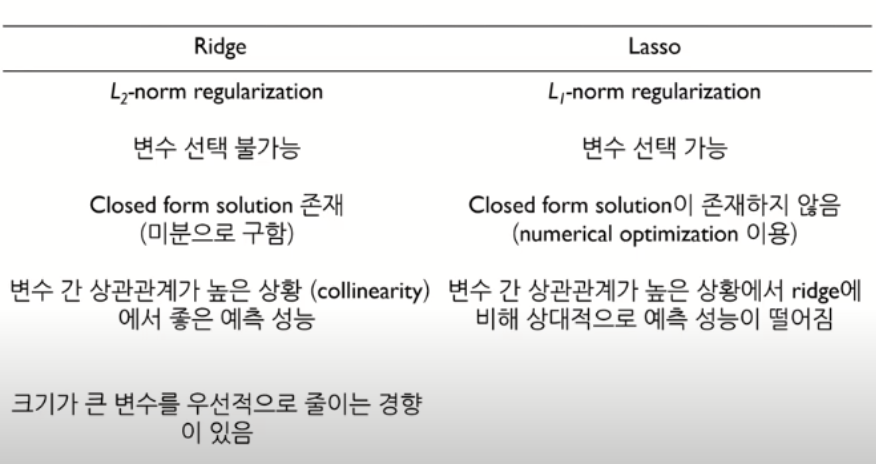
Number of Features: 1330

라쏘 회귀 (Lasso Regression, L1 Regression)


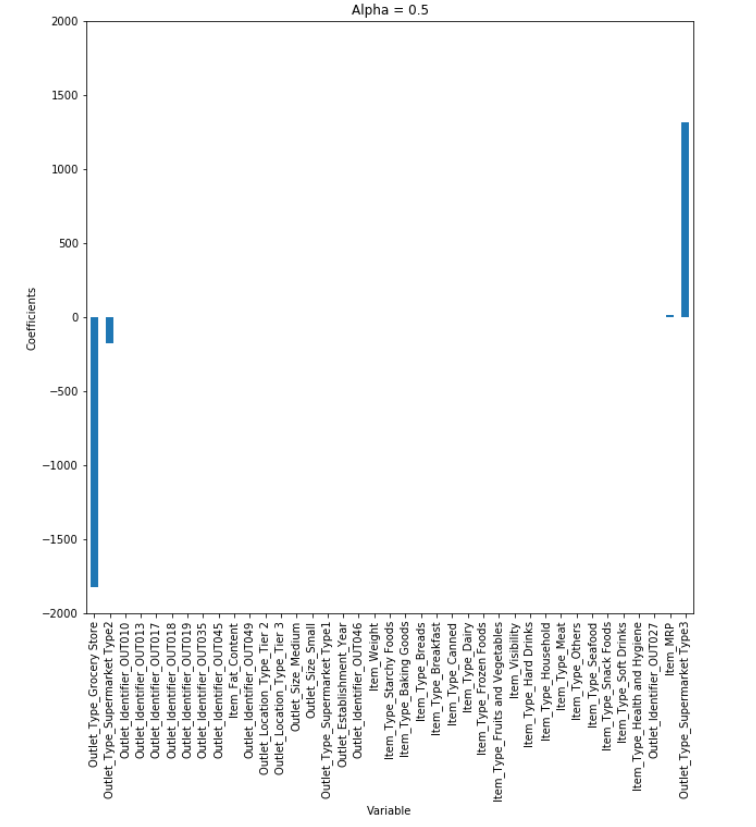
리지 회귀에서와 같이 라쏘(lasso)도 계수를 0에 가깝게 만들려고 합니다. 하지만 방식이 조금 다르며 이를 L1 규제라고 합니다. L1 규제의 결과로 라쏘를 사용할 경우 어떤 계수는 정말 0이 됩니다. 즉 모델에서 완전히 제외되는 특성이 생기는 것 입니다. 특성 선택이 자동으로 이루어진다고도 볼 수 있습니다. 일부 계수를 0으로 만들면 모델을 이해하기 쉬워지고 이 모델의 가장 중요한 특성이 무엇인지 드러내줍니다.

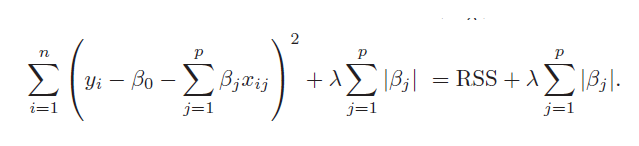
평균 오차 식(RSS) + λ∑j=1p∣βj∣\lambda\displaystyle\sum_{j=1}^{p} |\beta_j|
=> λ\lambda값을 크게 하면 패널티의 효과가 커집니다.(가중치 감소)

라쏘회귀는 릿지회귀와 비슷하게 생겼지만 패널티 항에 절대값의 합을 주었습니다. 라쏘회귀는 파라미터의 크기에 관계없이 같은 수준의 Regularization을 적용하기 때문에 작은 값의 파라미터를 0으로 만들어 해당 변수를 모델에서 삭제하고 따라서 모델을 단순하게 만들어주고 해석에 용이하게 만들어줍니다.




[reference]

릿지 회귀와 라쏘 회귀 쉽게 이해하기

profile
ssu_hyun
이전 포스트

n212_Multiple Regression

다음 포스트

n214_Logistic Regression

0개의 댓글