학습목표
- 예측모델을 위한 타겟을 올바르게 선택하고 그 분포를 확인할 수 있다.
- 테스트/학습 데이터 사이 or 타겟과 특성들간 일어나는 정보의 누출(leakage)을 피할 수 있다.
- 상황에 맞는 검증 지표(metrics)를 사용할 수 있다.
데이터 과학자 실무 프로세스
- 비즈니스 문제
- 실무자들과 대화를 통해 문제를 발견
- 데이터 문제
- 문제와 관련된 데이터를 발견
- 데이터 문제 해결
- 데이터 처리, 시각화
- 머신러닝/통계
- 비즈니스 문제 해결
- 데이터 문제 해결을 통해 실무자들과 함께 해결
문제와 데이터 이해
머신러닝 프로세스에서 가장 중요한 과정으로 데이터셋으로 무엇을 하는 것인지 머신러닝 모델을 만들기 전에 반드시 이해해야 하는 단계이다. 알고리즘마다 잘 들어맞는 데이터나 문제의 종류가 다르기 때문이다.
- 어떤 질문에 대한 답을 원하는가? 가지고 있는 데이터가 원하는 답을 줄 수 있는가?
- 내 질문을 머신러닝의 문제로 가장 잘 기술하는 방법은 무엇인가?
- 문제를 풀기에 충분한 데이터를 모았는가?
- 내가 추출한 데이터의 특성은 무엇이며 좋은 예측을 만들어낼 수 있을 것인가?
- 머신러닝 애플리케이션의 성과를 어떻게 측정할 수 있는가?
- 머신러닝 솔루션이 다른 연구나 제품과 어떻게 협력할 수 있는가?
지도학습(Supervised learning)_예측타겟 분석
테이블 형태의 데이터세트인 경우 어떤 특성을 예측타겟으로 할지 먼저 정해야 한다. 어떤 문제는 회귀/분류문제가 쉽게 구분이 안되는 경우도 있다.
- 이산형, 순서형, 범주형 타겟 특성도 회귀문제 또는 다중클래스분류 문제로도 볼 수 있다.
- 회귀, 다중클래스분류 문제들도 이진분류 문제로 바꿀 수 있다.
타겟을 정했다면 그 특성의 데이터타입(dtype), 분포(plot), 이진타입으로의 변형 유무 등을 확인해야 한다.
정보의 누수(leakage)
가끔 모델의 평가를 진행했을 때 예측을 100% 가깝게 잘 하는 경우가 있다. 이런 경우 좋아하기 보단 정보의 누수가 존재하는지 확인해볼 필요가 있다.
- 타겟변수 외에 예측 시점에 사용할 수 없는 데이터가 포함되어 학습이 이루어 질 경우
- 훈련데이터와 검증데이터를 완전히 분리하지 못했을 경우
이러한 경우 정보의 누수가 일어나 과적합이 일어나고 실제 테스트 데이터에서는 성능이 급격히 떨어지는 것을 확인할 수 있다.
https://www.fast.ai/2017/11/13/validation-sets/
#타겟 특성 제거하지 않고 훈련, 검증 세트 분할
from sklearn.model_selection import train_test_split
train, val = train_test_split(df, test_size=0.2, random_state=2)
train.shape, val.shape
from category_encoders import OrdinalEncoder
from sklearn.pipeline import make_pipeline
from sklearn.tree import DecisionTreeClassifier
target = 'recommend'
features = df.columns.drop([target, 'reviewDate'])
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
pipe = make_pipeline(
OrdinalEncoder(),
DecisionTreeClassifier(max_depth=5, random_state=2)
)
pipe.fit(X_train, y_train)
print('검증 정확도: ', pipe.score(X_val, y_val))평가지표 선택
예측모델의 평가지표를 선택할 때는 현재 내가 가진 문제의 상황이 어떠한지 정확하게 파악 후 이에 적합한 지표로 선택해야 한다. 특히 분류 & 회귀 모델의 평가지표는 완전히 다르다!
- Scikit-learn metrics : https://scikit-learn.org/stable/modules/model_evaluation.html#common-cases-predefined-values
- 분류(classification) metrics : https://scikit-learn.org/stable/modules/model_evaluation.html#classification-metrics
- 회귀(regression) metrics : https://scikit-learn.org/stable/modules/model_evaluation.html#regression-metrics
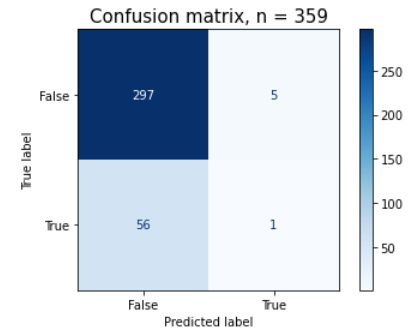
=> 상대적으로 True범주를 잘 못 맞히는데 검증 정확도는 높게 나온 경우
만약 내가 풀고자 하는 문제가 분류문제일 경우, 타겟 클래스비율이 70% 이상 차이 날 경우(불균형 클래스)에는 정확도만 사용하면 판단을 정확히 할 수 없고 정밀도, 재현율, ROC curve, AUC 등을 같이 사용해야 한다. 위 그림과 같이 목표값이 편중된 경우(클래스 불균형) 이진분류의 의미가 없어져 모델 성능에 대한 잘못된 판단을 할 수 있기 때문이다.


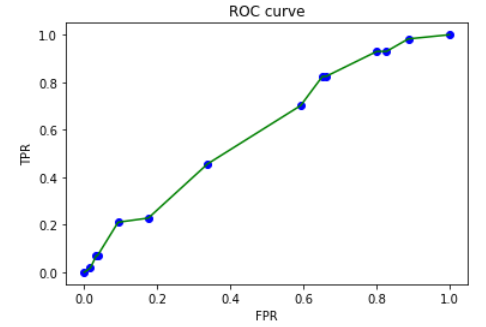
=> 검증정확도는 높게 나왔으나 True 지표에 대해 성능이 형편없으며 AUC score 또한 0.5에 가까운 것으로 보아 학습이 제대로 되지 않았음을 알 수 있다.
불균형 클래스
분류_타겟 특성 클래스 비율
위와 같이 (훈련 데이터) 타겟 특성의 클래스 비율이 차이가 많이 날 경우 이를 해결하는 방법은 2가지
1. 데이터가 적은 범주 데이터의 손실을 계산할 때 가중치를 더 곱하여 데이터의 균형을 맞추거나
2. 적은 범주 데이터를 추가샘플링(oversampling)하거나 반대로 많은 범주 데이터를 적게 샘플링(undersampling)하는 방법이 있다.
class_weight에서 원하는 비율을 적용하거나 class_weight='balance' 옵션 사용
# class weights 계산=>class_weight='balanced' 해당하는 계산
# 파이프라인을 만들어 봅시다.
pipe = make_pipeline(
OrdinalEncoder(),
# DecisionTreeClassifier(max_depth=5, class_weight='balanced', random_state=2)
DecisionTreeClassifier(max_depth=5, class_weight={False:custom[0],True:custom[1]}, random_state=2)
)
pipe.fit(X_train, y_train)
print('검증 정확도: ', pipe.score(X_val, y_val))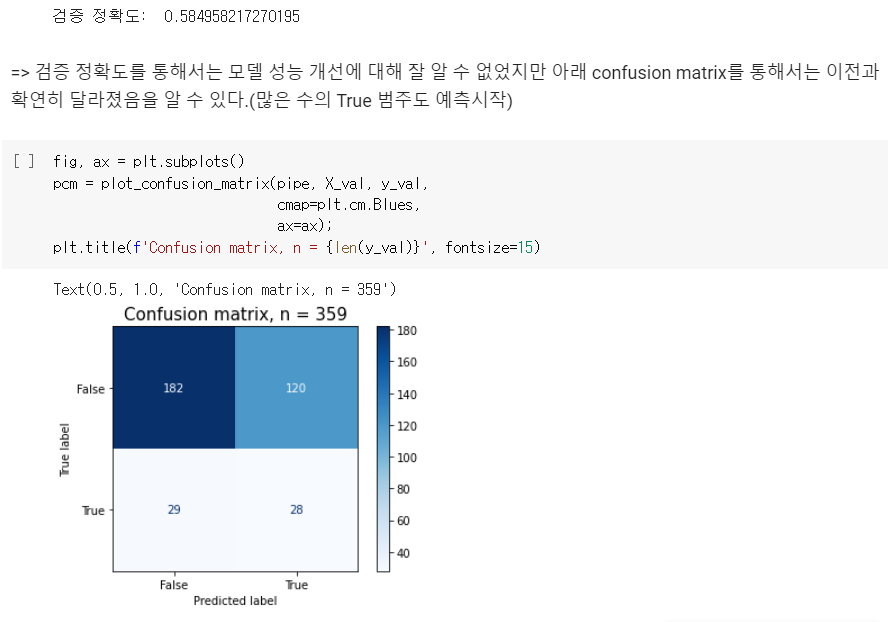

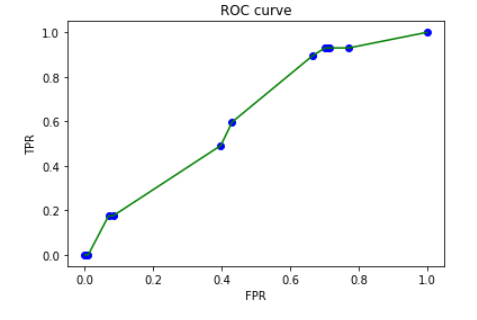
=> 이 데이터는 '추천하는 초콜릿을 맞추는 문제'였기 때문에 True 범주의 수치가 일괄 상승한 것은 성능이 대폭 상승한 것과 같음을 알 수 있다.
회귀_타겟 분포
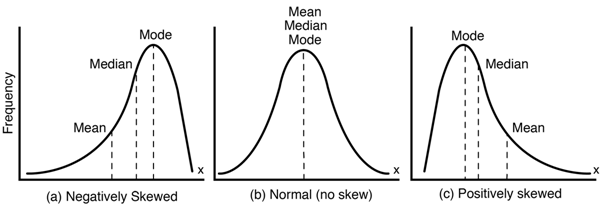
negatively : mean값 왼쪽으로 치우침
positively : mean값 오른쪽으로 치우침
일반적으로 선형 회귀 모델은 아래와 같은 특성이 있어
- 특성과 타겟간에 선형관계를 가정합니다.
- 그리고 특성 변수들과 타겟변수의 분포가 정규분포 형태일때 좋은 성능을 보인다.
타겟변수가 왜곡된 형태의 분포(skewed)일 경우 예측 성능에 부정적인 영향을 미치기 때문에 회귀분석에서는 타겟 분포가 비대칭 형태인지 꼭 확인해야한다.회귀에서 이러한 비대칭 형태를 해결하는 방식은 이상치 제거와 로그변환 2가지가 있다.
이상치 제거
## 몇몇 가격이나 다른 수치들은 은 너무 높아 문제가 될 수 있습니다.
import numpy as np
## 타겟 이상치(outlier)를 제거합니다.
df['SalePrice'] = df[df['SalePrice'] < np.percentile(df['SalePrice'], 99.5)]['SalePrice']
## 몇몇 변수를 합치고 이상치를 제거합니다.
df['All_Flr_SF'] = df['1stFlrSF'] + df['2ndFlrSF']
df['All_Liv_SF'] = df['All_Flr_SF'] + df['LowQualFinSF'] + df['GrLivArea']
df = df.drop(['1stFlrSF','2ndFlrSF','LowQualFinSF','GrLivArea'], axis=1)
df['All_Flr_SF'] = df[df['All_Flr_SF'] < np.percentile(df['All_Flr_SF'], 99.5)]['All_Flr_SF']
df['All_Liv_SF'] = df[df['All_Liv_SF'] < np.percentile(df['All_Liv_SF'], 99.5)]['All_Liv_SF']로그변환(Log-Transform)
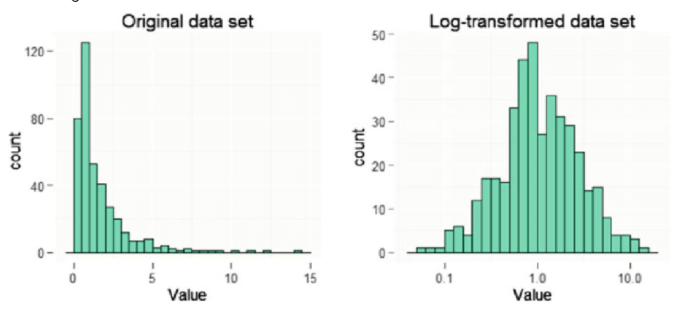
이는 비대칭 분포형태를 정규분포형태로 변환시켜준다.
log1p: ln(1 + x)
값의 변화로 해석에 문제가 생길 시, 역함수를 사용하여 이전의 값으로 되돌릴 수 있다.
expm1: exp(x) - 1, the inverse of log1p.
plots=pd.DataFrame()
plots['original']=target
plots['transformed']=np.log1p(target) #transform
plots['backToOriginal']=np.expm1(np.log1p(target)) #original 원상태로 transform
fig, ax = plt.subplots(1,3,figsize=(15,5))
sns.histplot(plots['original'], ax=ax[0]);
sns.histplot(plots['transformed'], ax=ax[1]);
sns.histplot(plots['backToOriginal'], ax=ax[2]);
TransformedTargetRegressor를 통해 한번에 타겟 분포 변경도 가능하다.
target = 'SalePrice'
from sklearn.model_selection import train_test_split
df = df[df[target].notna()]
train, val = train_test_split(df, test_size=260, random_state=2)
features = train.drop(columns=[target]).columns
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
from category_encoders import OrdinalEncoder
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestRegressor
from sklearn.compose import TransformedTargetRegressor
pipe = make_pipeline(
OrdinalEncoder(),
SimpleImputer(),
RandomForestRegressor(random_state=2)
)
tt = TransformedTargetRegressor(regressor=pipe,
func=np.log1p, inverse_func=np.expm1) #func->로그로 리턴, inverse_func->다시 원래로 바꿔줌
tt.fit(X_train, y_train)
tt.score(X_val, y_val)
[reference]
