High Dimensional Data
고유벡터 & 고유값
Eigenvector(고유벡터) : transformation을 통해 벡터가 다른 위치로 변하는데 이러한 transformation에 영향을 받지 않는 회전축(혹은 벡터)을 공간의 고유벡터라고 부른다
(주어진 transformation에 대해서 크기만 변하고 방향은 변하지 않는 벡터)
Eigenvalue(고유값) : 변화하는 크기는 스칼라 값인데 이 특정 스칼라 값을 고유값이라고 한다
고차원의 문제(The Curse of Dimensionality)
Feature의 수가 많은(100또는 1000이상) 데이터셋을 모델링하거나 분석할 때에 생기는 여러 문제
데이터셋에서 모든 feature가 동일하게 중요하지는 않다
데이터의 일부를 제한하더라도 의미 파악에는 큰 차이가 없다는걸 안다면 feature의 수와 관련하여 어느 시점에서는 feature를 더 사용하는 것이 비효율적이다
샘플 수에 비해서 feature의 수가 너무 많은 경우 overfitting의 문제가 생긴다
※ 이런 문제를 해결하기 위해 Feature Selection, Feature Extraction을 해야한다
차원축소(Dimension Reduction)
- Feature Selection : 100종류의 feature를 전부 사용하지 않고 데이터셋에서 제일 다양하게 분포되어있는 feature를 사용한다
장점 : 선택된 feature 해석이 쉽다 단점 : feature들간의 연관성을 고려해야함 - Feature Extraction : 기존에 있는 feature 또는 그들을 바탕으로 조합된 feature를 사용하는 것
장점 : feature들간의 연관성 고려됨 / feature 수 많이 줄일 수 있음 단점 : feature 해석이 어려움

PCA (Principal Component Analysis)
고차원 데이터를 효과적으로 분석하기 위한 기법
낮은 차원으로 차원 축소(Extraction 방법 중 하나)
원래 데이터의 정보(분산)를 최대한 유지하는 벡터를 찾고, 해당 벡터에 대해 데이터를 linear projection(정사영)
※ PCA(주성분 분석)은 데이터의 분산을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법이다
데이터의 분산(떨어진 정도) = 정보
즉 얼마나 떨어진 곳에 분포하는지가 정보이다
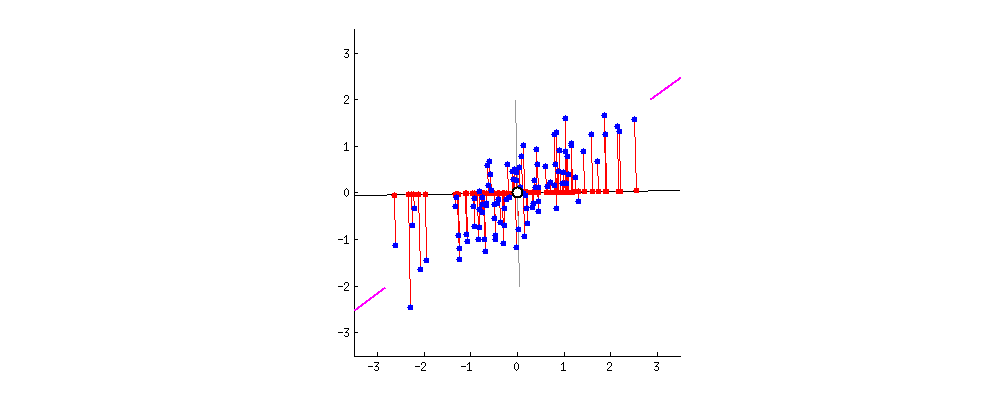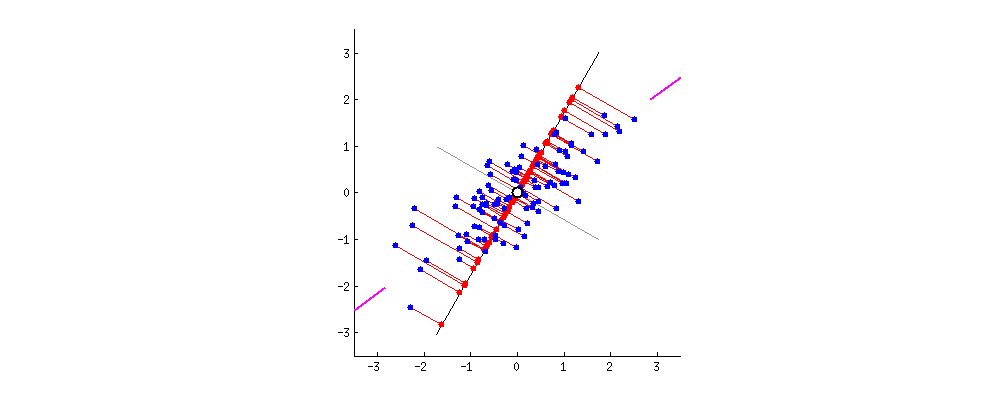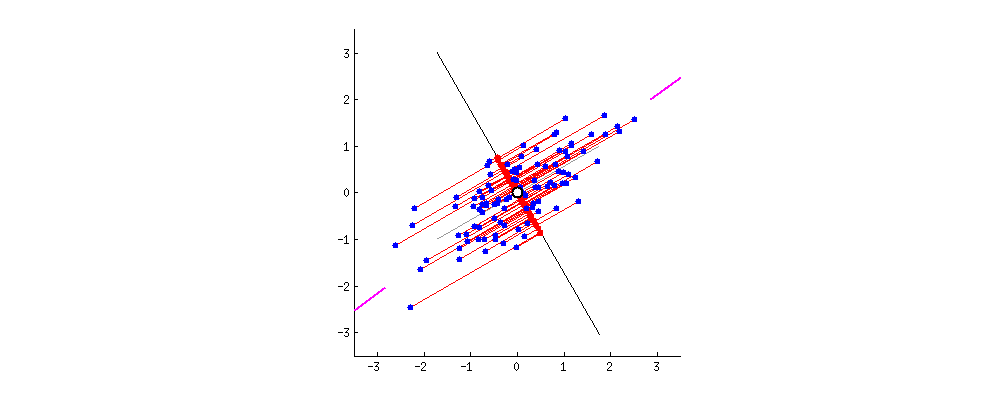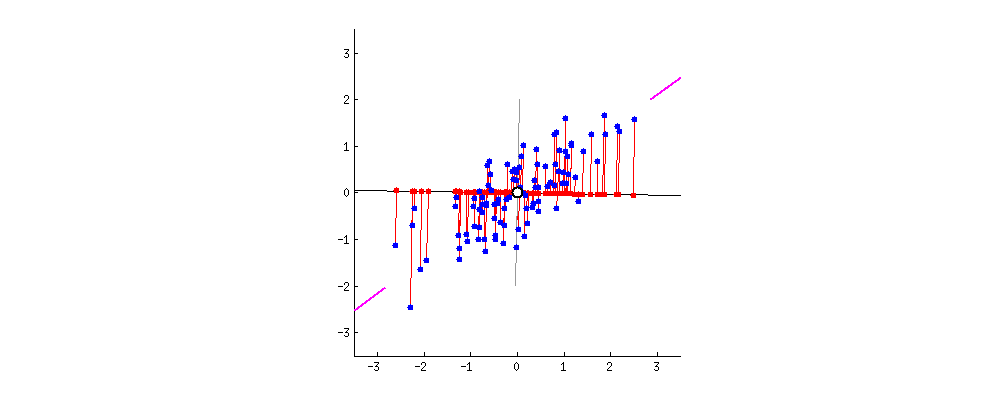
핑크색 표시가 돼 있는 사선축이 원 데이터의 분산을 최대한 보존하는(=데이터가 가장 많이 흩뿌려져 있는) 새 축이다
PCA의 목적이 이런 축을 찾는 것이다
다차원의 데이터를 시각화 하기 위해서 2차원으로 (scatter) 축소
그중에서 제일 정보 손실이 적은 2차원을 고른다
from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCA
scaler = StandardScaler() # 주어진 데이터를 표준화
Z = scaler.fit_transform(df)
pca = PCA(2) # 2차원
pca.fit(Z) # 표준화한 데이터에 적용
B = pca.transform(X)
df2 = pd.DataFrame(B, columns = ['PC1', 'PC2'], index = df.index)
sns.scatterplot(x = 'PC1', y = 'PC2', data = df2)
# PC1과 PC2에 대해서 scatter plot
# 여기서 PC1과 PC2는 무엇을 뜻하는지 알 수 없다
# 그저 어떠한 특성이다PCA의 특징
- 데이터에 대해 독립적인 축을 찾는데 사용 할 수 있음
- 데이터의 분포가 정규성을 띄지 않는 경우 적용이 어려움
(이 경우는 커널 PCA 를 사용 가능) - 분류 / 예측 문제에 대해서 데이터의 라벨을 고려하지 않기 때문에 효과적 분리가 어려움 (이 경우는 PLS 사용 가능)