역전파 / 경사하강법

1. 신경망 학습 알고리즘

① 데이터와 목적에 맞게 신경망 구조를 설계

• 입력층 노드 수 = 데이터의 Feature 수로 설정
• 출력층 노드 수 = 문제(분류, 회귀 등)에 따라 다르게 설정
• 은닉층 수와 각 은닉층의 노드 수를 결정

② 가중치를 랜덤하게 초기화
③ 순전파를 통해 출력값을 모든 입력 데이터에 대해 계산
④ 비용함수(Cost Function, J(θ))를 계산
⑤ 역전파를 통해 각 가중치에 대한 편미분 값을 계산
⑥ 경사하강법을 사용하여 비용함수인 J(θ) 를 최소화하는 방향으로 가중치를 갱신
⑦ 중지 기준을 충족하거나 비용 함수를 최소화 할 때까지 2~5단계를 반복(한번 반복 = iteration)

2. 비용함수(cost function) 손실함수(loss function)

신경망은 손실 함수를 최소화 하는 방향으로 가중치를 갱신한다(손실함수를 잘 정의 해야함)

• 입력 데이터를 신경망에 넣어 순전파를 거쳐서 출력층을 통과한 값이 도출
• 출력된 값과 그 데이터의 타겟값을 손실 함수에 넣어 손실(loss or error)를 계산
• 한 데이터 포인트에서 손실을 loss / 전체 loss를 합한 개념이 cost
• 대표적인 손실함수 MSE, cross-entropy 등이 있다
• 머신러닝보다 훨씬 많은 훈련 데이터가 필요해서 하이퍼파라미터 튜닝이 중요

3. 역전파(Backpropagation)

(Backpropagation : backwards propagation of errors)
순전파와 반대 방향으로 손실정보를 전달해주는 역할

• 손실정보를 출력층부터 입력층까지 전달하여 각 가중치를 얼마나 업데이트 해야할지를 결정하는 알고리즘
• iteration 마다 구해진 손실을 줄이는 방향으로 가중치를 업데이트
  손실을 줄이는 방향을 결정하는 것이 경사하강법(gradient descent)

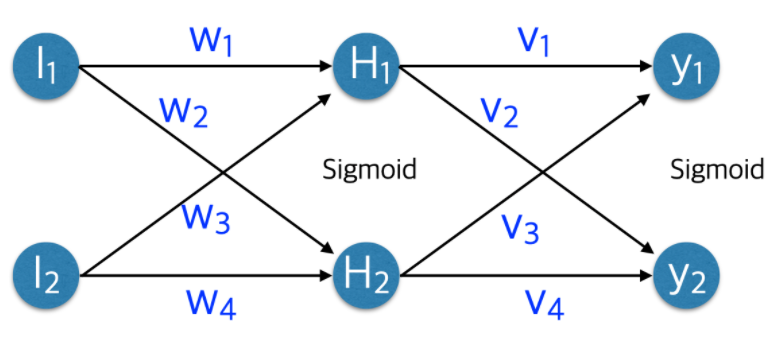
			가중치 w1, w2 업데이트
		     ⑤ w1 = X.T와 z2_delta의 곱
 w2 = layer1(은닉층) 활성화 함수의 함수값(activated_hidden)과 o_delta의 곱
 
                              입력값 X
                       Input : 2개   < I  I >
             w1 : layer1(은닉층)의 가중치 (shape 2X3)
---- ④ z2_delta = z2_error * 시그모이드 도함수(은닉층 활성화 함수의 함수값) ----
         ---- # dError/dh = (dError/dY)*(dY/dy)*(dy/dh)----
         
                      Hidden : 3개  < H  H  H >
      ---- ③ z2_error = o_delta와 layer2의 가중치(w2.T)의 곱 ----
         ---- #dError/dH = (dError/dY)*(dY/dy)*(dy/dH) ----
               w2 : layer2(출력층)의 가중치 (shape 3X1)
        ----② o_delta = o_error * 시그모이드 도함수(출력값) ----
            ---- #dError/dy = (dError/dY) * (dY/dy) ----
            
                        Output : 1개  < O >
                              출력값 o
        ---- ① o_error(타겟값 - 출력값 = 손실)  #dError/dY----
                              타겟값 y

✅ 역전파의 수학적 의미

$H_1 = I_1W_1+I_2W_3$
$H_2 = I_1W_2 + I_2W_4$
$y_1=H_1V_1 + H_2V_3$
$y_2=H_1V_2 + H_2V_4$

$\frac{\partial Error}{\partial v_1} = ①\frac{\partial Error}{\partial Y_1} * ②\frac{\partial Y_1}{\partial y_1} * ③\frac{\partial y_1}{\partial v_1}$ chain rule

① $Error = \frac{1}{2}(t_1-Y_1)^2 + \frac{1}{2}(t_2-Y_2)^2 \;\;\;\;Y_1$로미분

→ $\frac{\partial Error}{\partial Y_1}=-(t_1-Y_1)$

② = sigmoid 미분 = $f(x)(1-f(x))$ = $Y_1(1-Y_1)$

③ $y1 = H_1v_1+H_2v_3\;\;\;\;$ → $\;\;\;\; \frac{\partial y_1}{\partial v_1} = H_1$

4. 경사하강법

해당 함수의 최소값 위치를 찾기 위해 비용 함수(Cost Function)의 경사 반대 방향으로 정의한 Step Size를 가지고 조금씩 움직여 가면서 최적의 파라미터를 찾으려는 방법

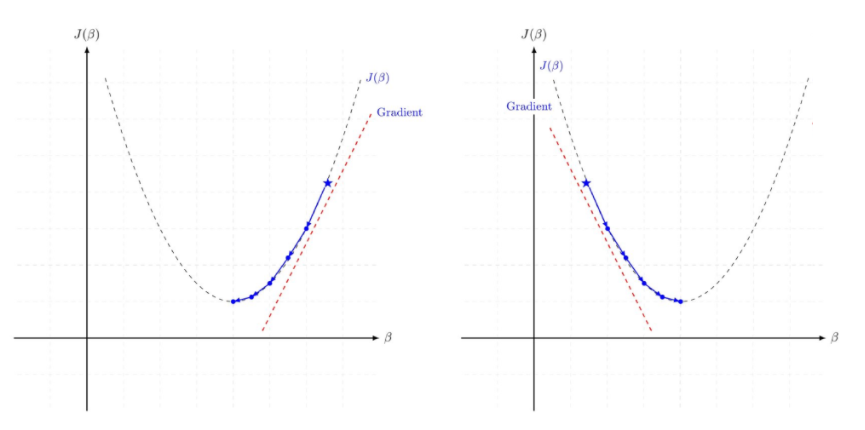
• 비용함수 J의 경사가 작아지는 방향으로 업데이트 하면 손실함수의 값을 줄일 수 있다
• 매 iteration 마다 해당 가중치에서의 비용 함수의 도함수(비용함수를 미분한 함수)를 계산하여 경사가 작아질 수 있도록 가중치를 변경
  
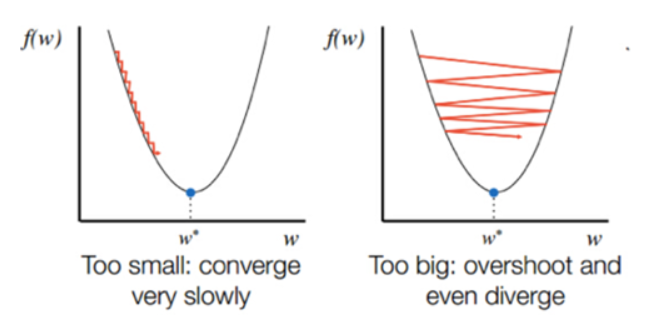
• 경사 하강법에서는 학습시 스텝의 크기 (step size)가 중요하다
• 학습률이 너무 작을 경우 알고리즘이 수렴하기 위해 반복해야 하는 값이 많으므로 학습 시간이 오래걸리고 지역 최소값(local minimum)에 수렴할 수 있다
• 반대로 학습률이 너무 클 경우 학습 시간은 적게 걸리나, 스텝이 너무 커서 전역 최소값(global minimum)을 가로질러 반대편으로 건너뛰어 최소값에서 멀어질 수 있다

※ 경사 하강법을 통해 최저점을 찾는 메커니즘은 볼록 함수에서만 잘 동작한다
※ 실제 손실함수는 볼록과 오목함수가 섞여있어서 전역최적점(global optima)를 찾지 못하고 지역최적점(local optima)에 빠질 수 있다

확률적 경사 하강법(Stochastic Gradient Descent, SGD)

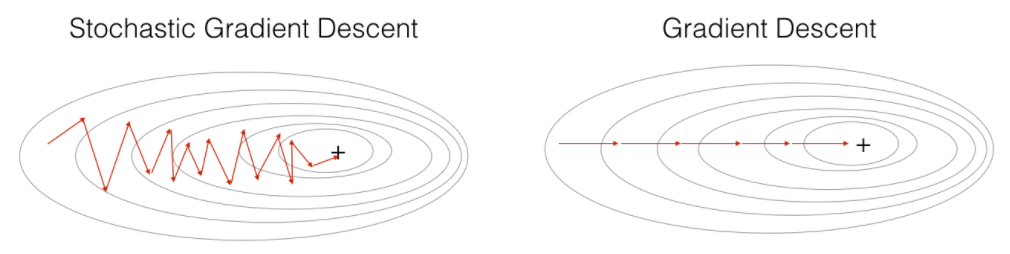
• 확률적 경사 하강법(sgd)은 전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산합니다. 그리고 그 손실 정보를 역전파하여 신경망의 가중치를 업데이트하게 된다
• 확률적 경사 하강법은 1개의 데이터만 사용하여 손실을 계산하기 때문에 가중치를 빠르게 업데이트 할 수 있다는 장점이 있지만 1개만 보기 때문에 학습 과정에서 불안정한 경사 하강을 보인다

미니배치 경사 하강법

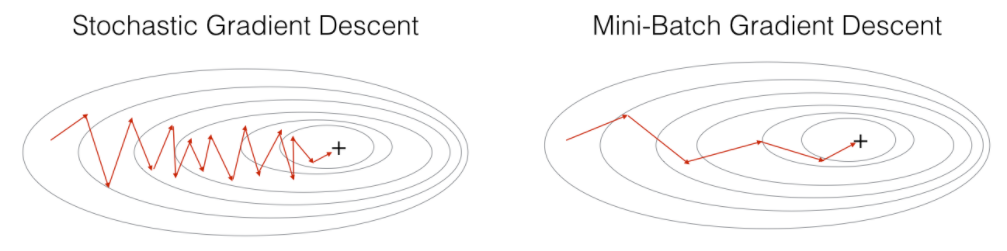
• 확률적 경사하강법 + 경사하강법을 적절히 융화한 방법
• N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력 후 결과를 바탕으로 가중치를 업데이트 한다. 일반적으로 미니배치 경사하강법을 많이 이용한다

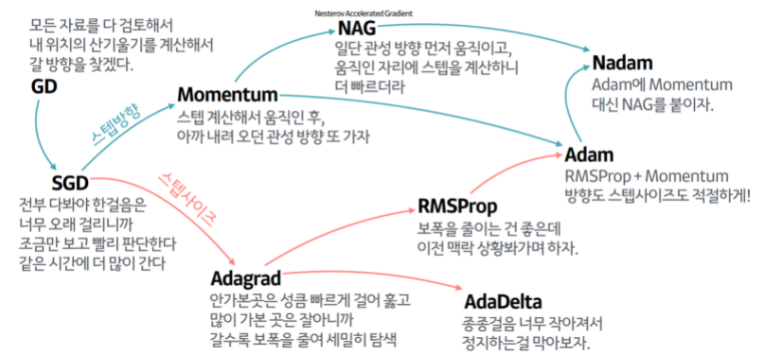
5. 옵티마이저

지역 최적점에 빠지게 되는 문제를 방지하기 위한 여러가지 방법 중 하나
경사를 내려가는 방법을 결정하는 알고리즘

---

6. Keras를 이용한 역전파

신경망 학습 메커니즘
1. 학습 데이터 로드(Load data)
2. 모델 정의(Define model)
3. 컴파일(Compile)
4. 모델 학습(Fit)
5. 모델 검증(Evaluate)

1. 학습 데이터 만들기
X_train, y_train

2. 신경망을 구축하고 compile
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
 
model = Sequential()

# 신경망 모델 구조 정의
model.add(Dense(3, input_dim=2, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))

model.compile(optimizer='sgd',
		   loss='mse',
           	   metrics=['mae', 'mse'])
# 분류인 경우
model.compile(loss='binary_crossentropy',
			optimizer='adam',
            		metrics=['accuracy']) 

results = model.fit(X_train,y_train, epochs=50)