[Data] 데이터 전처리 - '이상치(Outlier)와 결측치(Missing Value) 처리하기

데이터 분석을 진행하다보면 전처리 과정이 제일 중요하다는 것을 깨닫게 될 때가 많다. 다양한 데이터를 접하면서 가장 고민이 되는 부분이 해당 데이터의 '이상치'와 '결측치'를 어떻게 처리하는지이기 때문에 이제부터 다양한 처리 방법에 대해 알아보자!

📝 이상치와 결측치

• 이상치(Outlier) : 보통 관측된 데이터의 범위에서 많이 벗어난 아주 작은 값이나 큰 값을 말한다.

• 결측치(Missing Value) : 데이터 수집 과정에서 측정되지 않거나 누락된 데이터를 말한다.

  이상치와 결측치는 모두 데이터 전처리 과정에서 처리를 진행해주지 않으면
  데이터 분석에 큰 영향을 끼치게 되기 때문에 알맞은 처리를 진행해주어야 한다!

  
  

📝 이상치(Outlier) 탐지방법

1. Standard Deviation (정규분포)

데이터의 분포가 정규 분포를 이룰 때, 데이터의 표준 편차를 이용해 이상치를 탐지하는 방법이다.

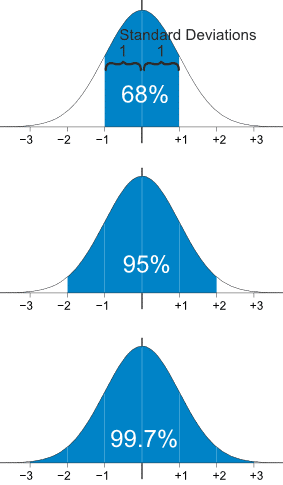
💡 68-95-99.7 규칙 (3시그마 규칙)

• 1표준편차 : 약 68%의 값들이 평균에서 양쪽으로 1 표준편차 범위(μ±σ)에 존재한다.

• 2표준편차: 약 95%의 값들이 평균에서 양쪽으로 2 표준편차 범위(μ±2σ)에 존재한다.

• 3표준편차: 거의 모든 값들(실제로는 99.7%)이 평균에서 양쪽으로 3표준편차 범위(μ±3σ)에 존재한다.

  즉, 그래프의 정해진 표준편차마다 각각 파란 부분을 넘어서는 부분에 해당하는 값들을 이상치로 보는 방법이다.

  
  
  

💡 Z-score 공식

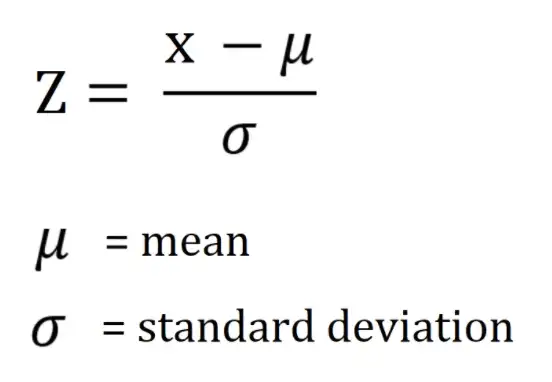
• Z-score: 해당 데이터가 평균으로부터 얼마의 표준 편차만큼 벗어나 있는지를 의미한다.
• 3 표준 편차 만큼을 벗어나는 데이터를 이상치로 처리하는 것은 Z-score 가 3 보다 크고 -3 보다 작은 데이터를 이상치로 처리하는 것과 같은 작업이다.
  
  
  
  

2. IQR (Interquartile Range) with Box plots

데이터의 분포가 정규 분포를 이루지 않거나 한 쪽으로 skewed 한 경우, 데이터의 IQR 값을 이용해 이상치를 탐지하는 방법이다.

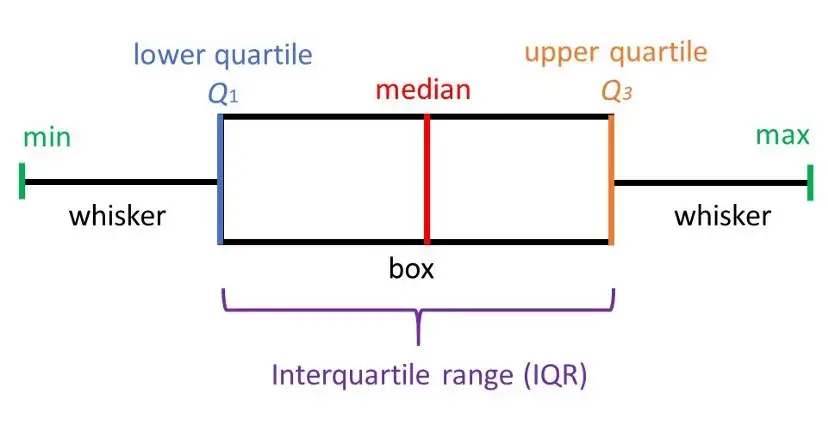
• 최솟값 : 제 1사분위(Q1)에서 1.5 IQR을 뺀 위치이다.

• 제 1사분위(Q1) : 25%의 위치를 의미한다.

• 제 2사분위(Q2) : 50%의 위치로 중앙값(median)을 의미한다.

• 제 3사분위(Q3) : 75%의 위치를 의미한다.

• 최댓값 : 제 3사분위에서 1.5 IQR을 더한 위치이다.

• IQR : (제 3사분위 값) - (제 1사분위 값)

즉, (Q1 – 1.5 IQR) 보다 작거나 (Q3 + 1.5 IQR) 보다 큰 데이터는 이상치로 처리하며, 1.5 보다 큰 3 혹은 그 이상의 값을 곱하기도 하며 값이 클수록 더욱 최극단의 이상치를 처리함을 알 수 있다.

3. Isolation Forest

결정 트리 계열의 비지도 학습 알고리즘으로 High dimensional 데이터셋에서 이상치를 탐지할 때 효과적인 방법이다.

* High dimensional 데이터셋: 변수(혹은 피처)의 수가 매우 큰 데이터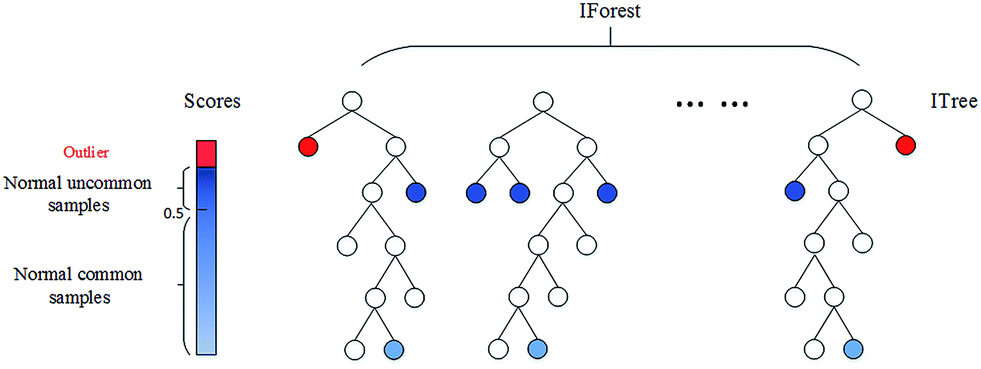

• 데이터셋을 결정 트리 형태로 표현해 정상 데이터를 분리하기 위해서는 트리의 깊이가 깊어지고 반대로 이상치는 트리의 상단에서 분리할 수 있다는 개념을 이용한다.
• 즉, 데이터에서 이상치를 분리하는 것이 더 쉽다는 것이다.

<이상치가 아닌 데이터>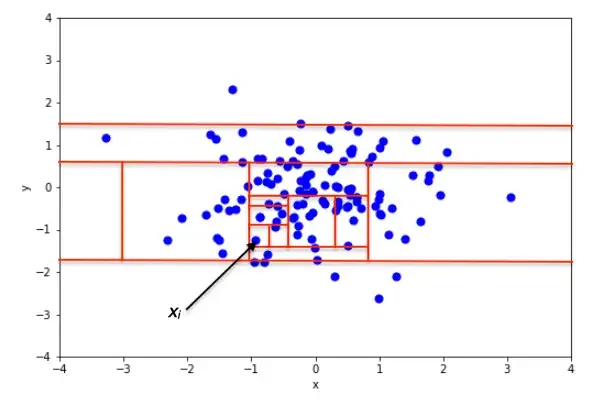

<이상치 데이터>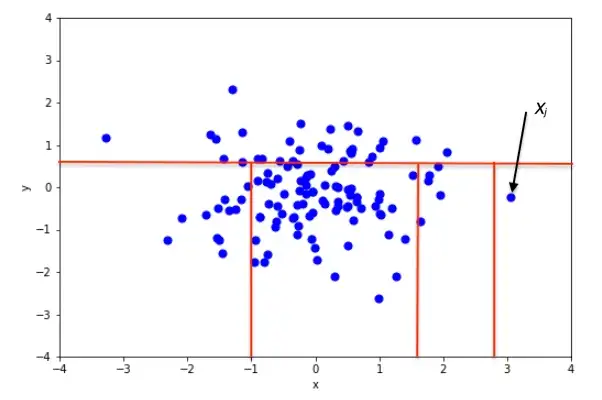

• 이상치 판단 방법

  • 특정 데이터를 데이터셋에서 분리하기 위해선 트리에서 몇 번을 분리해야 하는지 (데이터까지의 경로 길이)를 기준으로 데이터가 이상치인지 아닌지를 판단한다.

  • 이상치는 다른 관측치에 비해 짧은 경로 길이를 가진 데이터일 것이다.

  • 이러한 개념을 기반으로 각 데이터에 대해 이상치 점수를 부여할 수 있으며 공식은 다음과 같다.

    

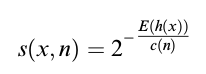
h(x)는 경로 길이로 점수는 0 에서 1 사이로 산출된다. 결과가 1 에 가까울수록 이상치로 간주된다.

4. DBScan (Density Based Spatial Clustering of Applications with Noise)

밀도 기반의 클러스터링 알고리즘으로 어떠한 클러스터에도 포함되지 않는 데이터를 이상치로 탐지하는 방법이다.

💡 DBScan 알고리즘의 2가지의 하이퍼파라미터

• eps : 두 데이터 사이의 거리가 eps 보다 작거나 같을 때 이들은 같은 클러스터 내에 있는 것으로 간주한다.
• MinPts : 한 클러스터 내에 존재해야 하는 데이터의 최소 개수. 최소 3 이상의 값을 가져야 하며 보통은 데이터의 차원에 1을 더한 값 이상으로 설정한다.

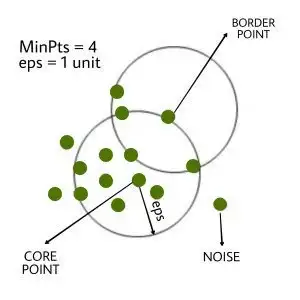
eps 거리 내에 MinPts 이상의 데이터를 이웃하는 데이터는 Core Point 가 되고 반대로 eps 거리 내에 MinPts 미만의 데이터를 이웃하는 데이터는 Border Point 가 된다. 그리고 이들을 제외한 데이터가 바로 이상치(Noise)가 된다.

📝 이상치(Outlier) 처리 방법

1. 상한값과 하한값

• 하한값과 상한값을 결정한 후 하한값보다 적으면 하한값으로 대체, 상한값보다 크면 상한값으로 대체함

2. 평균의 표준편차

• 하한값 = 평균 - n*표준편차
• 상한값 = 평균 + n*표준편차
• 일반적으로 3시그마 (99.7% 이상 혹은 이하값을 이상치로 제거하거나 대체)

3. 평균 절대 편차

• 중위수로부터 n편차 큰 값을 대체

4. 극 백분위수

• 상위 p번째 백분위수보다 큰 값을 대체

📝 결측치(Missing Value) 처리방법

1. 행 또는 열 삭제

• 결측치가 존재하는 행 또는 열(feature)을 삭제

2. 중앙값, 평균값으로 대체

• 빈 결측치에 해당하는 Feature의 평균값이나 중앙값으로 대체

3. 최빈값으로 대체

• 주로 Nominal feature(범주형 feature)일 때 유용한 방법

4. XGboost, LightGBM 사용

• use_missing=False 인자를 첨가하면 알고리즘이 알아서 Training loss에 기반해 결측치를 채우게 된다.

5. K-NN알고리즘을 사용

• 결측치의 값을 가장 가까운 즉, feature similarity를 적용하면서 대체
• 이상치(outlier)에 민감하다는 단점이 존재한다.

6. MICE(Multivariate Imputation by Chained Equation)

• 결측치를 한 번 대체하는 게 아니라 여러번(multi) 대체해보면서 결측치의 불확실성(uncertainty)을 체크하면서 결측치를 대체
• 이산, 연속 변수에도 flexible하게 사용되는 장점이 있다.

7. 딥러닝

• 딥러닝을 적용해 학습시켜 알아서 최적의 결측치를 찾는 것
• 주로 Categorical feature에 유용하며 다른 방법들에 비해 꽤 정확하다.
• 대용량의 데이터에는 속도가 느리다.
• 만약 결측치가 존재하는 feature가 여러개라면 여러개를 동시에 딥러닝에 적용은 못하고 하나의 feature씩만 impute할 수 있다.
• 또한 결측치가 존재하는 칼럼들의 정보를 갖고 있는 다른 칼럼들을 사용자가 직접 지정해주어야 한다는 단점이 있다. (즉, 하이퍼파라미터 튜닝이 필요하다.)