[통계학] 다중회귀분석과 로지스틱 회귀분석

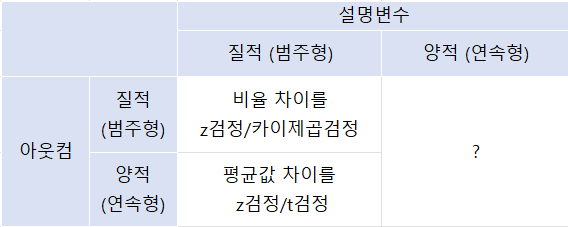
       양적변수 분석을 위해서는 '양적 설명변수가 늘 때마다 평균적으로 얼마만큼 
       아웃컴이 느는가/주는가'라는 경향성을 나타내는 분석방법을 사용하고
       이것이 바로 '회귀분석'이다.

📒 회귀분석

• 산포도와 회귀직선으로 '경향' 파악

  • 산포도 : 가로, 세로축에 양적 항목을 잡고 점을 그려넣은 그래프
  • 경향성 : '경향성을 나타내는 직선과 실제 데이터 값을 벗어난 값의 제곱합'을 최소로 만드는 직선 (최소제곱법)
  • 평균값으로 회귀 : 예언된 변인에서 극단적인 값을 가져야 될 사람이 덜 극단적인 예언된 특성을 지니는 경향성

📒 회귀직선과 회귀식

• 회귀직선의 구성 (단순회귀)

  • 회귀계수(β1) : 설명변수(X)가 증가할 때 아웃컴(Y)가 몇 단위로 늘어나고 줄어드는지를 나타내는 '기울기'

  • 절편(β0) : 설명변수(X)가 0인 경우, 아웃컴(Y)의 값이 몇이 되는지를 나타낸 값

• 최소제곱법의 활용

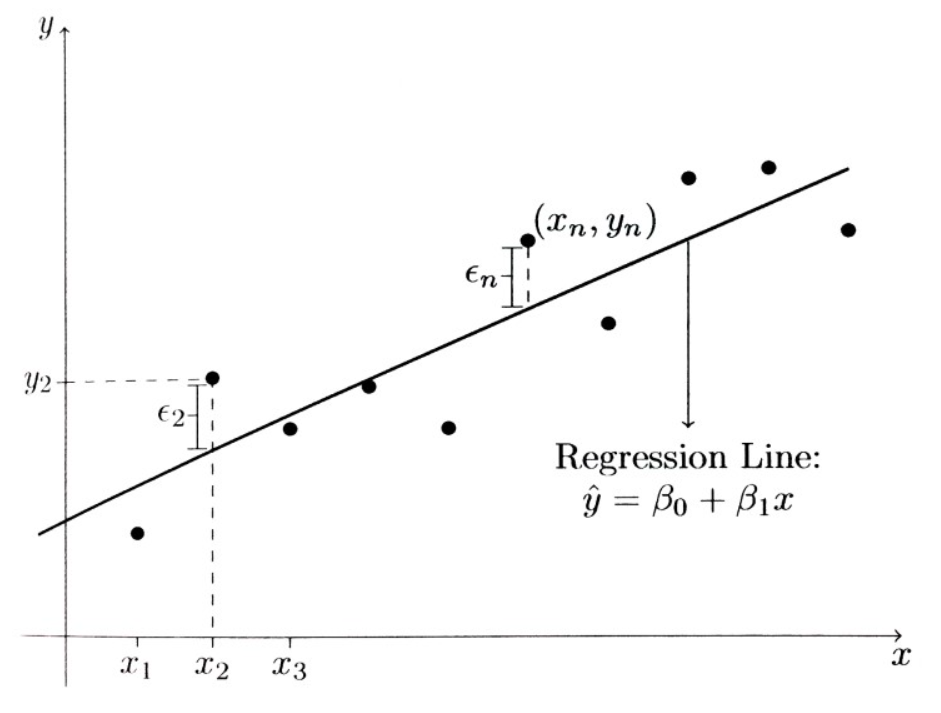
  • 최소제곱법을 사용하여 회귀직선을 구할 때는, 각각의 점에 대해 '실제의 아웃컴(Y)의 값'과 'X값과 회귀식에서 구해지는 아웃컴(Y)의 예측값'의 세로축 방향 차이의 제곱합을 최소화

  • 잔차제곱합 : 회귀직선에서 벗어난 값들의 차이 제곱의 합 (ε1+ε2+ε3+...+εn)을 의미하며 이 값이 가장 작아질 때 최량의 회귀직선으로 생각

• 회귀분석 결과

  • 회귀계수와 절편의 값을 모를 때 임의로 a, b로 설정한 후, 아웃컴의 회귀직선에 의한 예측값과 실제값 차이의 제곱합을 최소화하는 a, b 조합이 무엇인지를 찾는 것이 회귀분석의 결과

  • a, b에 대한 편미분으로 잔차제곱합이 최소가 되는 a, b값 계산 가능

• 회귀계수의 표준오차 (기울기의 표준오차) ★★★

  • 우연에서 발생한 경향성을 고려하기 위해 회귀분석에서는 회귀계수의 표준오차(SE)를 생각한다

  • 회귀계수의 표준오차 : 많은 양의 데이터를 모으기만 하면 알 수 있는 '진정한 회귀계수'가 존재한다고 할 때, 얼마만큼의 건수, 그리고 어떤 불규칙성이 있는 데이터에 의해 그것을 추정하려 든다면 어느 정도의 불규칙성이 나타나겠는가를 의미한다.

  • 회귀계수도 중심극한정리가 성립한다

    • 수많은 데이터로 회귀분석 시행시, 100회의 데이터 수집과 분석을 통해 산출되는 회귀계수의 95회 정도는 '진정한 회귀계수±2SE' 의 범위에 수용
    • '실제 얻어진 회귀계수±2SE'의 범위 밖에 진정한 회귀계수가 존재하는 귀무가설은 양쪽 5%의 유의수준에서 있을 수 없다로 판명

  • 데이터의 양이 적을 경우 t분포의 사용이 낫다는 것 또한 동일

  • 평균값의 표준오차와의 차이점

    • 평균값의 표준오차
      1. 편차제곱합(평균값에서 벗어난 값의 제곱합) 사용
      2. 분산 = 편차제곱합 / 데이터의 수
    • 회귀계수의 표준오차
      1. 잔차제곱합(아웃컴의 예측값과 실제 값의 차이를 제곱한 합을 데이터수로 나눈 것) 사용
      2. 평균제곱잔차 = 잔차제곱합 / 데이터의 수

  • 회귀계수의 표준오차 계산에 추가로 필요한 것

    • '아웃컴(Y)의 예측값과 실제 값이 평균적으로 어느 정도 벗어나 있는가'라는 크기를, 설명변수(X)가 어느 정도 불규칙한지의 크기에 대한 비율로 상대적 판단을 해야한다
    • 회귀계수의 표준오차
      = √(잔차제곱합)/(설명변수의 편차제곱합 * 데이터수)

📒 다중회귀분석

• 단순회귀분석 : 하나의 설명변수와 아웃컴의 관련성을 보기 위한 회귀분석

  • 설명변수와 아웃컴의 관계성에 대해 산포도에는 나타내지 못한 간과한 사실들이 있음

  • 서브그룹 해석 : 이를 해결하기 위해 데이터를 각각의 설명변수들로 나눠 분할된 그룹(서브그룹)과 아웃컴과의 관계성을 분석하는 것

    • but 데이터의 크기가 커지면 한계 존재 (서브그룹내의 평균 인원이 적어져 오차가 커짐)

• 다중회귀분석 : 복수의 설명변수와 아웃컴의 관련성을 '한번에 분석'

  • 최소제곱법 사용

  • 설명변수가 질적변수인 경우

    • 0과 1로 표현되는 '이항변수'의 형태로 변경 → 더미변수

• 회귀분석, z검정, t검정의 결과가 일치하는 이유 ★★

  • 최소제곱법에 근거하여 그려진 회귀직선은 두 질적변수 집단들의 양적변수의 평균값을 나타내는 점을 지난다.

  • 두 값의 설명변수에서 회귀계수는 z검정이나 t검정에서 생각했던 '그룹 간 평균값 차이'와 완전히 동일

    • 평균값 차이의 표준오차
      '각 그룹 값의 분산' : 그룹 각각의 값과 평균값의 차이에서 벗어난 값의 제곱의 평균값

    • 회귀계수의 표준오차
      '평균제곱잔차' : 회귀직선에서 벗어난 값의 제곱의 평균값인데, 회귀직선이 그룹별 평균값을 지나기 때문에 이역시 '평균값에서 벗어난 값의 제곱의 평균값'이라고 할 수 있음

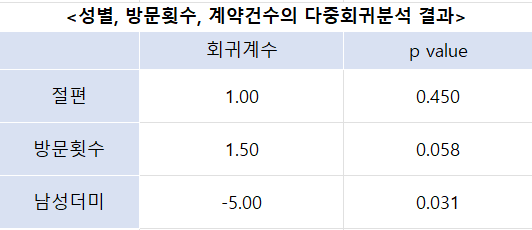
		1) 여성더미의 회귀계수는 -5 
          : 방문횟수가 같으면 남성은 여성에 비해 평균적으로 계약건수가 5건 적다
        
        2) 방문횟수 회귀계수는 1.50
          : 성별의 조건이 같다면 방문횟수가 1회 늘 때마다 평균 1.5회씩 계약건수가 
            많아지는 경향을 보인다.
        
        3) 성별과 계약건수의 p-value는 0.031
          : 이 정도의 데이터만 가지고도 우연이라고 말하기 어렵다
          
        4) 방문횟수와 계약건수의 p-value는 0.058
          : 5%를 믿도는 수준이 아니므로 인원수를 조금 더 늘려서 분석하면 우연이라고 
            말하기 어렵다는 결과가 나올 수 있다.
            

• 실무에서는 모든 설명변수를 다중회귀분석에 적용하여 p값이 작고 회귀계수가 큰 것을 탐색하는 방식을 압도적으로 선호함!

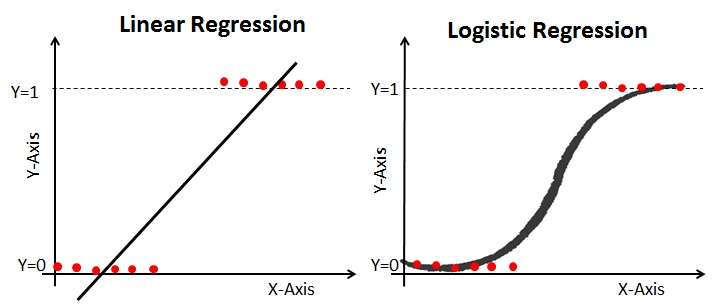
📒 로지스틱 회귀분석과 로그오즈비

• 로지스틱 회귀분석 : 이항논리에 관한 아웃컴을 분석하는 회귀분석
  

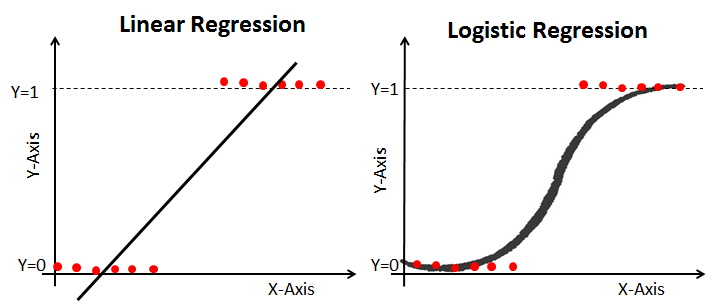
  • 질적인 아웃컴에 대해 단순회귀분석인지 다중회귀분석인지 구분하지 않는다.

• 오즈 (odds) : 어떤 상황을 취하는 확률에 대해 '확률 / (1-확률)'

  • 해당자의 비율이 낮은 질적 아웃컴에 대해 그 확률을 좌우할 가능성이 있는 요인을 조사할 때 중요한 의미
    

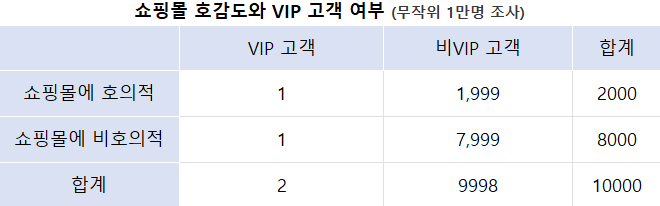
  • 귀무가설 아래서 모든 칸에 5~10명이 해당이라는 z검정이나 카이제곱검정의 조건 만족 불가능

  • 케이스 컨트롤 (case control) 조사 필요

    • 케이스 : 질병의 사례 (발병한 사람들의 그룹)

    • 컨트롤 : 비교 대조 (조건이 동일한데도 발병하지 않은 그룹)

    • 조건이 동일한데도 병에 걸린 사람과 걸리지 않은 사람 사이에 어떤 차이가 있는지 살펴보는 것 → 오즈비 필요

    • 오즈비는 VIP 고객률이 그룹간에 약 몇 배 다른지를 잘 나타내는 지표

    • 오즈비를 활용하면 임의추출법이든 케이스 컨트롤이든 결과가 일치

      

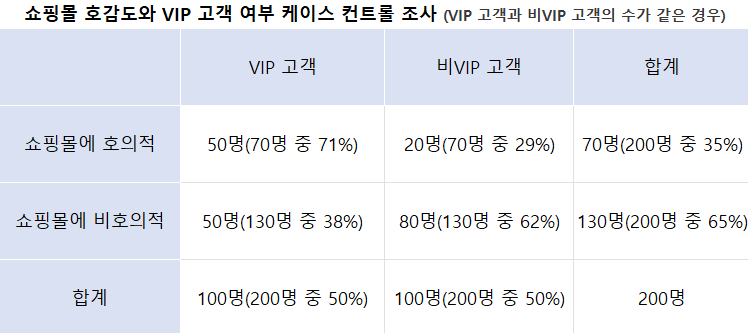
       - 쇼핑몰에 호의적인 사람의 'VIP 고객 오즈' = 50/70÷(1-50/70) = 2.5
        - 쇼핑몰에 비호의적인 사람의 'VIP 고객 오즈' = 50/130÷(1-50/130) = 0.625
        - 쇼핑몰에 호의적인 오즈비는 4.00배(=2.5÷0.625)로 'VIP 고객의 확률이 높다'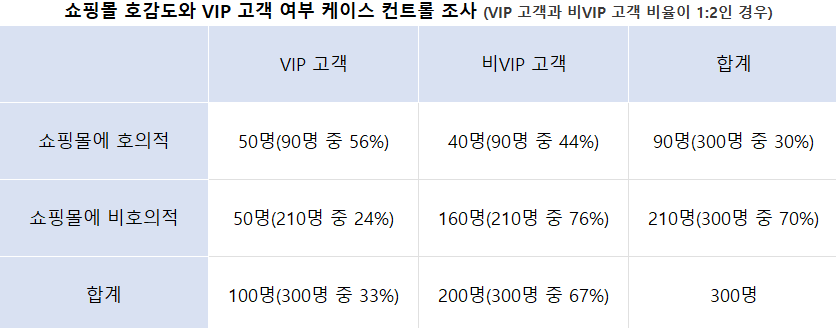
       

      

      - 쇼핑몰에 호의적인 사람의 'VIP 고객 오즈' = 50/90÷(1-50/90) = 1.25
       - 쇼핑몰에 비호의적인 사람의 'VIP 고객 오즈' = 50/210÷(1-50/210) = 0.3125
       - 쇼핑몰에 호의적인 오즈비는 4.00배(=1.25÷0.3125)로 'VIP 고객의 확률이 높다'

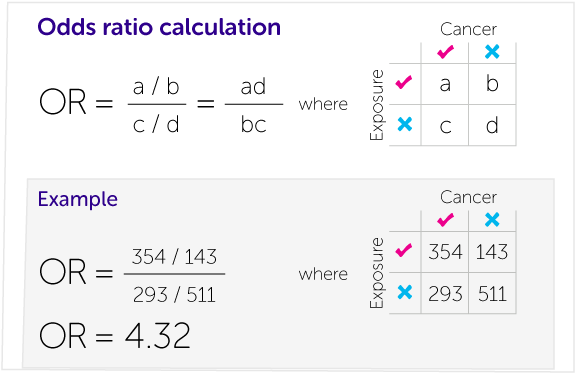
- 오즈비 (odds ratio) : 그룹간의 오즈의 비율

• 로그오즈비 : 오즈비에 로그를 취한 값

• 로짓변환 : 오즈비에 로그를 취해 값을 변환하는 것

  • 로그오즈비를 사용하면 0과 1의 값만 취하는 이항의 아웃컴이 다중회귀 분석의 양적인 아웃컴과 마찬가지로 -∞부터 +∞까지의 값을 나타내도록 변환할 수 있다.

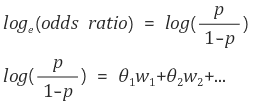
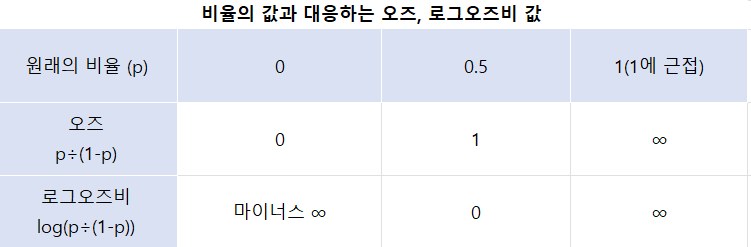
• 회귀계수 변환
  • 대응하는 설명변수에 회귀계수의 '로그' 부분 제외
  • 네이피어수 ^ 회귀계수
    : 설명변수가 1 증가할 때마다 아웃컴이 1이 되는 비율이 약 몇배인가에 관한 값

    ex. VIP고객인가(1) VIP고객이 아닌가(0) 아웃컴에 관한 로지스틱 회귀분석
    	
        - 남성더미의 회귀계수 = 2.00
    	- 오즈비 = 2.718(네이피어수)^2 = 7.39
    	- 남성이 여성에 비해 약 7.39배 아웃컴이 1이 되기 쉽다
        
        

📒 회귀모형 정리

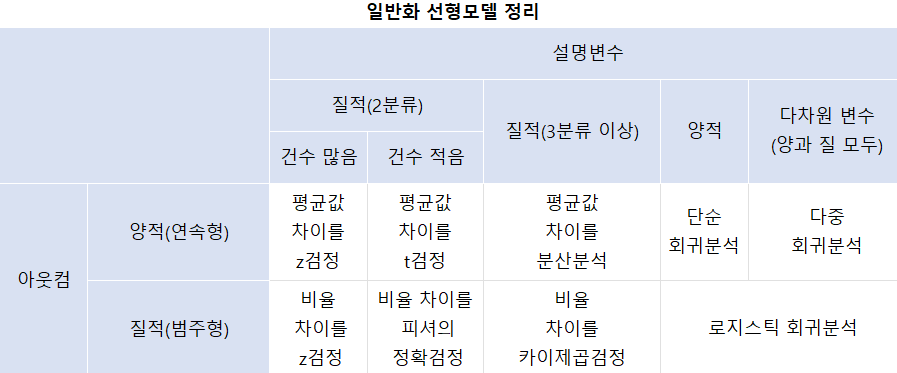
📒 다중회귀분석 vs 로지스틱 분석

• 아웃컴이 셋 이상의 카테고리로 나뉘는 경우

  1. 다중회귀분석

  • 각 카테고리의 차이가 모두 동일하다고 판단한 경우

  2. 로지스틱 회귀분석

  1) 이항변수화 (목적에 따라 아웃컴 설정)

  • '매우불만' 응답고객을 줄이고 이탈방지와 클레임 대책 반영
    : 전혀 만족하지 않는다(1), 만족하지 않는다(0)
  • '매우만족' 응답고객을 늘리고 브랜드 파워나 SNS 활용 입소문
    : 매우 만족한다(1), 만족한다(0)
  • 둘다 중요한 경우
    : 둘다 분석하고 회귀계수(오즈비) 중 어디가 같고 다른지 고찰
    

  2) 순서형 로지스틱 회귀분석 (이유없이 사용 권장 x)

  • 이항변수와 하지 않고 '0~3'점 만족도 점수채로 분석
  • 이 또한 다중회귀와 마찬가지로 차이가 모두 동일하다는 가정
  
  

• 설명변수와 아웃컴의 관계성이 직선이 아닌 경우

  1) 물리학 or 계량경제학

  • 회귀곡선으로 계산
  • '제곱항' (본래의 설명변수를 제곱한 새로운 설명변수)의 회귀계수
  • 본래의 설명변수와 제곱항을 모두 설명변수로 갖는 다중회귀분석

  2) 의학연구나 비즈니스

  • 기준 카테고리를 정하고 더미변수 설정

📒 회귀모형의 실제 활용법

• 과적합

  : 설명변수가 증가할수록 예측값에서 벗어난 잔차가 작아지게 되어 잔차가 관계가 없어야 하는 설명변수의 불규칙성과 닮아있게 되는 경우

• 과적합 문제

  : 새롭게 적용하는 데이터를 회귀식에 적용시키면 적합도가 나빠진다

• 과적합 해결방법

  • 변수선택법 : 의미있는 설명변수만 회귀식에 포함

    • 전진선택법

     1) 후보가 되는 설명변수 모두에 대해 단순회귀분석
      2) 회귀계수의 p값이 가장 작은 설명변수를 첫번째 설명변수로 채택
      3) 이외의 설명변수를 하나씩 조합하여 2개의 설명변수를 
         포함하는 다중회귀모형들을 분석
      4) 다중회귀모형들 중 두번째로 추가되는 설명변수의 회귀계수에 
      대응하는 p값이 가장 작은 설명변수 채택하고 이 변수를 두번째 회귀모형에 추가
      5) p값이 0.05 이내라면 계속 반복하며 최종 회귀식 도출

    • 후진제거법