📗'통찰'의 통계학을 위한 3가지 지식
1) 평균과 비율의 본질적 이해
'평균'과 '비율'은 기본적으로는 완전히 동일한 개념
WHY?
- 비율과 평균은 다른 계산방법이 존재하는 것이 아님
- 수의 형태로 표현할 수 없는 질적변수에 대해서 각 분류마다 1이나 0이라는 형태로 '해당하는 정도'라는 양적변수를 생각하여 평균을 계산하는 것
평균: 양적변수(나이, 수입, 구매금액과 같이 숫자로 표현되는 정보)
비율: 질적변수(성별, 직업, 상품 분류와 같이 문자로 표현되는 정보)
※ 1과 0같은 형태로 표현할 수 있는 변수 중 양적변수와 질적변수의 특징을 모두 가지는 변수는 이항변수
→ 동일한 개념이긴 하지만, 변수의 형태에 따라 쓰임이 차이가 나는 것!
2) 데이터가 존재하는 '구간'
- 통계학에선'데이터는 대체로 어디에서 어디까지의 범위에 속해있는가?'하는 식의 구간으로 파악하는 방법을 고안함
- 데이터를 평균이나 비율과 같은 '점'이 아닌 '구간'으로 이해하는 지혜가 - 중요
3) '결과'와 '원인'의 압축
"무슨 값을 어떻게 정리해야 하는가?"
- 인과관계: 어떤 원인에 의해 결과가 어떻게 변하는지 알아내는 것
- outcome(성과지표) : 최종적으로 조절하고 싶은 결과 (결과변수, 목적변수, 종속변수, 외적기준 등으로 불림)
- 설명변수: outcome에 영향을 달리 미칠 수 있거나 차이를 설명할 수 있을지 모르는 요인
- output: outcome과는 다른 뜻으로, 의미있는 결과가 아닌 단순한 결과와 관련한 표현 (ex. 광고인식률, SNS 입소문 건수는 단지 과정일 뿐, 업종이나 상품에 따라서는 이익과 전혀 관계가 없을 수 있음)
💡비즈니스에서 가치있는 분석은 '최대화하거나 최소화해야 하는 항목'이 무엇인지 알아내는 것 (=outcome을 정하고 그와 관련된 데이터를 분석)
< 설명변수의 우선순위 설정 >
: 아웃컴과 연관된 설명변수들이 많다고 생각하는 경우 우선순위를 중심으로 데이터를 분석하면 효율적
- 너무나도 당연한 인과관계이면 안될 것
- 아웃컴에 명백한 영향을 미치는 변수더라도 조절 가능한 것이어야 할 것
- 이제까지 주목 받지 않고 분석된 적이 별로 없어야 할 것
📗'평균'의 본질
'통찰'을 위한 통계학에서는 중앙값과 최빈값에 신경쓰는 일이 거의 없다
WHY?
중앙값은 참값에서 벗어난 값(차이, 절댓값)의 총합을 최소로 만드는 신뢰할 수 있는 추측값이지만 계산의 불편함이 매우 크다
이를 해결하기 위해 고안한 방법이 최소제곱법!
- 최소제곱법 : '차이의 제곱'을 모두 더했을 때 가장 작은 값을 '참값'으로 추정한다 (평균은 최소제곱법에 기초하여 측정값에 포함되어 있는 차이를 가장 적게 만드는 추정값)
📗평균으로 진실을 포착할 수 있는 이유
1) 인과관계의 통찰 관점에서 볼때, 평균이 중앙값보다 관심이 있는 것에 대한 직접적인 대답이 되는 경우가 많다
- 전체적인 매출이 얼마나 변했는가 하는 증감을 알기 위해선 평균이 적합
2) 데이터의 불규칙성이 정규분포를 따르고 있으면, 최소제곱법이 가장 좋은 추정 방법이고 그 결과 평균값이 가장 좋은 추정값이 된다
[ 정규분포 ]
좌우대칭인 매끄러운 곡선으로 표현되는 데이터의 불규칙성
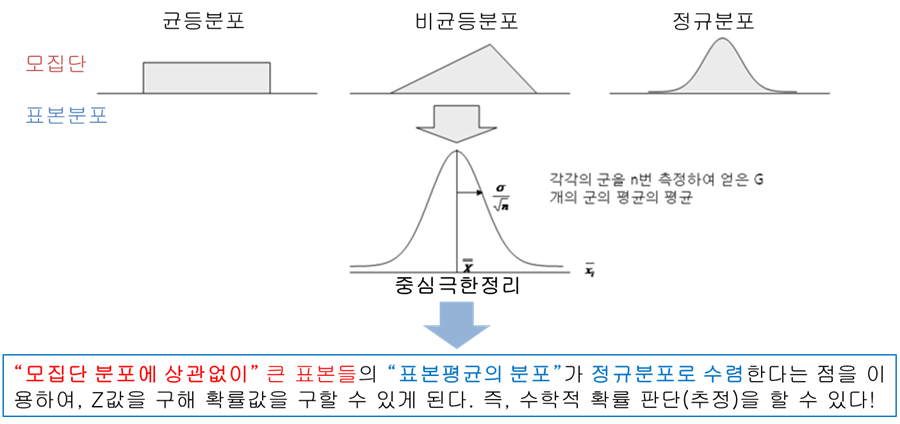
[ 중심극한정리 ]
'대다수 데이터가 정규분포를 따른다'는 사실을 넘어 어떤 데이터가 정규분포를 따르지 않는다고 해도 '데이터 값을 거듭 추가할수록' 정규분포에 수렴하게 된다는 것
📗표준편차로 '데이터의 대략적 범위' 파악
현상파악 시 사용하는 방법
1) 최댓값 & 최솟값
- 1건에 데이터에 의해 대푯값이 정해지는 단점
2) 사분위수 : 25%, 중위값, 75%
- 데이터 정렬이나 수식을 전개하기 어렵고, 총량의 차이를 계산하기 쉽지 않음
3) 분산 : 데이터의 펼쳐진 정도
- '참값에서 벗어난 값의 제곱합'은 데이터가 늘수록 커질 수 밖에 없으므로, 데이터가 늘수록 불규칙성이 커지게 되는 현상 발생
- 이를 해결하기 위해, '벗어난 값의 제곱합' 대신 '벗어난 값의 제곱 평균'을 사용하여 내포된 불규칙성 표현
- 불편성 갖는 분산인지에 대한 여부는 신경쓸 필요 없음
4) 표준편차: 분산에 제곱근을 씌운 값
- 분산은 벗어난 값을 제곱한 상태 그대로를 생각하는 지표이기 때문에 이미지를 더 잘 잡고 싶다면 제곱 처리 필요
평균과 표준편차의 현상분석
데이터의 불규칙성이 어떠하든, < 평균값-2SD ~ 평균값+2SD >까지의 범위에 반드시 전체의 4분의 3이상의 데이터가 존재한다
