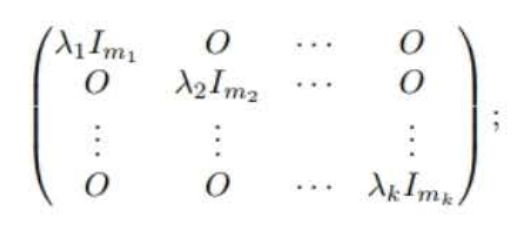0. 직합
직합이란 공간을 간단한 부분공간으로 분해하는 방법 혹은 부분공간을 하나의 공간으로 합치는 방법이다.
정의 벡터공간 V의 부분공간 W1,W2,…,Wk에 대하여 다음 집합을 부분공간의 합이라 한다.
{v1+v2+⋯+vk:1≤i≤k,vi∈W}
이때 벡터공간 V를 W1+W2+⋯+Wk로 표현할 수 있다.
이때 이러한 부분공간의 표현은 유일하지 않다. 즉, 다양한 부분공간의 조합으로 합을 표현할 수 있다. 하지만 다음 정의를 이용하면 유일한 부분공간의 합이 가능하다.
정의 벡터공간 V의 부분공간 W1,W2,…,Wk을 생각하자. 모든 i=1,2,…,k에 대하여 Wi⊆W이고 다음을 만족하는 W를 부분공간 W1,W2,…,Wk의 직합(direct sum)이라 하며 W=W1⊕W2⊕⋯⊕Wk로 표기한다.
W=∑i=1kWi이고, 각 j(i≤j≤k)에 대하여 Wj∩∑j=iWi={0}
즉 각 부분집합이 독립적이면서 부분집합의 합이 본 공간이 될 경우 이를 직합이라 한다.
1. 정사영
우선 사영에 대해 이야기를 해보자.
정의 벡터공간 V에서 V=W1⊕W2일 때, 혹은 모든 x∈V에 대하여 x=x1+x2(x1∈W1,x2∈W2)일 때 T(x)=x1인 선형연산자 T를 W2에 대항 W1위로의 사영이라 한다.
또한 이전에 행렬의 공간에 대해 이야기 하면서 R(T)=W1={x∈V:T(x)=x},N(T)=W2이므로, V=R(T)⊕N(T)라 이야기하여도 문제가 없음을 알 수 있다. 이때 T가 사영이기 위한 필요충분조건은 T=T2이어야 한다.
주의해야할 점은 V=W1⊕W2=W1⊕W3라 하여서 W2=W3를 보장하지 않는다는 것이다. 즉, W1은 T를 유일하게 결정하지 않는다. 하지만 이제 다룰 정사영은 치역에 의해 유일하게 결정되는 연산자이다.
정의 내적공간 V와 사영 T:V→V를 생각하자. R(T)⊥=N(T),N(T)⊥=R(T)를 만족하는 T를 정사영(orthogonal projection)이라 한다.
만약 V가 유한차원일 경우 위 정의에서 사용된 수식 중 하나만 성립해도 될 것이다. 왜냐하면 R(T)⊥=N(T)이면 자동으로 R(T)=R(T)⊥⊥=N(T)⊥으로 성립하게 되기 때문이다. 이 반대역시 당연히 성립하게 된다.
정사영과 직교연산자가 비슷해보일 수도 있는데, 엄연히 다른 개념이다.
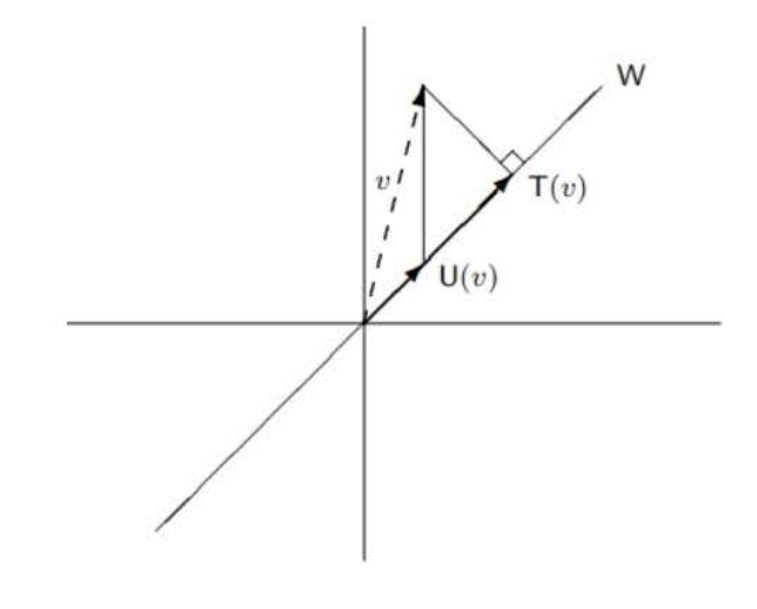
위 그림에서 T는 W 위로의 정사영이지만 직교연산자는 될 수 없다. 직교연산자는 놈을 보존하는데 ∣∣T(v)∣∣=∣∣v∣∣이기 때문이다.
이제 정사영이 유일함을 보이자.
증명
내적공간 V의 유한차원 부분공간 W를 생각하자. 이때 T:V→V를 T(y)=u로 표기하자. 이때 T가 W로의 정사영이라면, 유일한 정사영이다. 만약 T와 U가 모두 정사영이라면 R(T)=W=R(U)이어야 한다. 이는 N(T)=R(T)⊥=R(U)⊥=N(U)로 된다. 이때 사영은 치역과 영공간에 의해 유일함이 결정되므로 T=U가 된다. 즉, T가 W로의 V의 정사영일 때 이는 유일하다.
1.1 사영과 정사영
이제 사영과 정사영의 차이점에 집중해보자.

위에서 사용된 상황을 그대로 사용하자. V=R2,W=span{(1,1)}일 때, U와 T가 위와 같다. 이때 T(v)는 v에서 y=x에 내린 수선의 발이고, U(a1,a2)=(a1,a1)이다. T는 그림에서 볼 수 있듯이 W로의 V의 정사영이고, U는 W로의 사영이다. 이때 v−T(v)∈W⊥이지만, v−U(v)∈W⊥이다.
좀 더 자세히 이야기하면, T(v)는 v가 W와 가장 가까운 점을 이은 W로의 최적근사이다. 즉, w∈W,∣∣w−v∣∣≥∣∣T(v)−v∣∣로 표현할 수 있다. 이는 선형회귀나 차원 축소 등에서 중요한 성질로 사용된다.
이제 정사영의 가장 중요한 특징을 보도록 하자.
정리 내적공간 V와 선형연산자 T를 생각하자. T가 정사영이기 위한 필요충분조건은 T의 수반연산자 T∗가 존재하고 T2=T=T∗가 성립하는 것이다.
증명
T가 정사영이라 가정하자. T는 당연히 사영이므로 T2=T를 만족할 것이다. 이때, T∗가 존재하면서 T=T∗만 보이면 된다.
T가 정사영이므로 V=R(T)⊕N(T),R(T)⊥=N(T)가 된다. x,y∈V에 대하여 x=x1+x2,y=y1+y2로 표현할 수도 있을 것이다(x1,y1∈R(T),x2,y2∈N(T)). 이제 식을 정리하여 다음이 가능하다.
<x,T(y)><T(x),y>=<x1+x2,y1>=<x1,y1>+<x2,y1>=<x1,y1>=<x1,y1+y2>=<x1,y1>+<x1,y2>=<x1,y1>
즉 모든 x,y∈V에 대하여 <x,T(y)>=<T(X),y>이므로 T∗가 존재하고 T=T∗임을 알 수 있다.
이제 T2=T=T∗임을 보이자.
T2=T=T∗이라 가정하자. 이는 곧 T가 사영임을 의미한다. 이제 R(T)=N(T)⊥,R(T)⊥=N(T)임을 보이자. 이를 통해 정사영임을 밝힐 수 있을 것이다. x∈R(T),y∈N(T)에 대하여 x=T(x)=T∗(x)이고 다음이 성립한다.
<x,y>=<T∗(x),y>=<x,T(y)>=<x,0>=0
즉, x∈N(T)⊥이므로 R(T)⊆N(T)⊥이 성립한다.
이제 y∈N(T)⊥에 대하여 y∈R(T)를 보이자. 즉, T(y)=y면 된다.
∣∣y−T(y)∣∣2=<y−T(y),y−T(y)>=<y,y−T(y)>−<T(y),y−T(y)>=<y,0>−<T(y),y−T(y)>=−<T(y),y−T(y)>=−<y,T∗(y−T(y))>=−<y,T(y−T(y))>=−<y,0>=0
즉, y−T(y)=0이 될 것이다. 또한, y=T(y)∈R(T),R(T)=N(T)⊥이 될 것이다.
자 이제 조금 정리를 해보자. 이제 우리는 R(T)⊥=N(T)⊥⊥⊇N(T)임을 알 수 있다. 이제 x∈(T)⊥이라 가정하면, 임의의 y∈V에 대하여 <T(x),y>=<x,T∗(y)>=<x,T(y)>=0이 성립한다. 결과적으론 T(x)=0,x∈N(T)임을 보이게 되는 것이다.즉, R(T)⊥=N(T)이다.
이제 대각화와 연결해보도록 하자. 유한차원 내적공간 V, 부분공간 W, W로의 V의 정사영 T를 생각하자. {v1,v2,…,vk}가 W의 기저가 되도록 V의 정규직교기저 β={v1,v2,…,vn}을 잡으면, [T]β는 첫 k개 대각성분이 1이고, 나머지 성분은 0인 대각행렬 꼴이 된다. 즉, 다음과 같은 모양이다.
(IkO2O1O3)
U가 W로의 임의의 사영일 때, [U]γ가 위의 꼴이 되도록하는 V의 기저 γ를 잡을 수 잇지만, γ가 정규직교인지 보장할 수는 없게 된다.
2. 스펙트럼 정리
자 이제 거의 다 왔다.
정리 스펙트럼 정리
유한차원 F-내적공간 V의 선형연산자 T의 서로 다른 고유값을 λ1,λ2,…,λk라 하자. F=C이면, T는 정규연산자, F=R이면 T가 자기수반연산자라 가정하자. 각 i(1≤i≤k)에 대하여 고유값 λi에 대응하는 고유공간을 Wi라 표기하자. Wi로의 V의 정사영을 Ti라 할 때 다음이 성립한다.
1. V=W1⊕W2⊕⋯⊕Wk
2. j=i에 대하여 부분공간 Wj의 직합을 Wi′로 표기하자. Wi⊥=Wi′이다.
3. 1≤i,j≤k에 대하여 TiTj=δijTj이다.
4. I=T1+T2+⋯+Tk
5. T=λ1T1+λ2T2+⋯+λkTk
증명
-
T가 정규연산자 혹은 자기수반연산자이기 위한 필요충분조건은 정규직교기저 β가 존재하는 것이다. 이를 이용하면 T는 대각화가능하고, 결국 V=W1⊕W2⊕⋯⊕Wk로 나타낼 수 있다.
-
i=j에 대해 x∈Wi,y∈Wj라 해보자. 이때, 정규연산자의 성질에 의해 <x,y>=0이 되고, Wi′⊆Wi⊥이 된다. 이때 Wi′의 차원은 다음과 같다.
dim(Wi′)=i=j∑dim(Wi)=dim(V)−dim(Wi)
이때, dim(Wi⊥)+dim(Wi)=dim(V)이므로 dim(Wi⊥)=dim(V)−dim(Wi)가 성립한다. 즉, Wi′=Wi⊥이다.
-
각 고유 공간은 서로 직교한다. 이를 이용하면 i=j일 때 x∈V에 대하여 <T1(x),T2(x)>=0임을 알 수 있다. 반대로 i=j라면, <T1(x),T2(x)>=1이다.
-
Ti가 Wi로의 V의 정사영이기 때문에, N(Ti)=R(Ti)⊥=Wi⊥=Wi′가 된다. 즉, x∈V에 대하여 x = x_1 + x_2 + x_3 + \dots + x_k$이다.
-
x∈V를 x=x1+x2+⋯+xk라 표기하자. 이때 다음이 성립함을 보일 수 있다.
T(x)=i=1∑kT(xi)=i=1∑kλixi=i=1∑kλiTi(x)=(i=1∑kλiTi)(x)
즉 선형연산자 T는 T의 고유값과 그 고유값에 대응하는 정사영의 선형결합으로 표현할 수 있다. 이를 스펙트럼 분해라고 한다.
이때 T의 고유값으로 이루어진 집합 {λ1,λ2,…,λk}를 T의 스펙트럼이라 한다. 네번째 성질인 I=T1+T2+⋯+Tk를 T로 유도된 항등연산자 분해라 하고, 다섯번째 성질에서 나오는 T=(∑i=1kλiTi)를 T의 스펙트럼 분해라고 한다. 만약 고유값의 배열순서를 무시한다면 T의 스펙트럼 분해는 유일하다고 할 수 있다.
Wi의 정규직교기저의 합집합을 β, 차원을 mi이라 하자. 이때 [T]β는 다음과 같은 꼴이 된다.
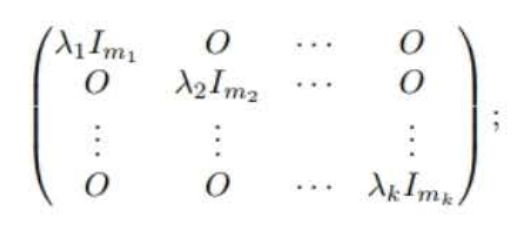
즉, [T]β는 중복도가 mi인 고유값 λi를 대각성분으로 하는 대각행렬이 된다. T의 스펙트럼 분해가 λ1T1+λ2T2+…λkTk라 하면, 어떤 다항식 g에 대해 g(T)=g(λ1)T1+g(λ2)T2+…g(λk)Tk가 성립하게 된다.
마지막으로 네가지 따름 정리를 살펴보도록 하자.
따름정리 1
F=C일 때, T가 정규연산자이기 위한 필요충분조건은 적절한 다항식 g에 대하여 T∗=g(T)인 것이다.
증명
T가 정규연산자라 가정하고, T의 스펙트럼 분해를 T=∑i=1kλiTi라고 하자. 이때 이 식의 양변에 수반연산자를 취하면, Ti는 자기수반연산자이기 때문에, T∗=∑i=1kλiˉTi가 될 것이다. 이때 라그랑주 보간법을 사용하여 1≤i≤k에 대해 g(λi)=λiˉ인 다항식 g를 찾을 수 있다. 이를 이용해 다음 식이 성립하게 된다.
g(T)=i=1∑kg(λi)Ti=i=1∑kλiˉTi=T∗
이제 T가 정규연산자라면 T∗=g(T)인 적절한 다항식이 존재함을 알았다. 역으로 어떤 다항식 g에 대하여 T∗=g(T)라 가정하면, T는 T에 대한 임의의 다항식과 가환적이기 때문에, T는 T∗가환적이다. 즉, T는 정규연산자라 볼 수 있다.
따름정리 2
F=C일 때, T가 유니타리 연산자이기 위한 필요충분조건은 T가 정규연산자이고, T의 모든 고유값 λ가 ∣λ∣=1인 것이다.
증명
T가 유니타리 연산자라면 자연스레 정규연산자이다. 유니타리 연산자의 성질로 인해 T의 모든 고유값은 절대값이 1임을 간단히 알 수 있다.
또한, T의 스펙트럼 분해를 T=∑i=1nλiTi라고 하자. 이때 T의 고유값의 절대값이 모두 1이라면 다음이 성립한다.
TT∗=(i=1∑nλiTi)(i=1∑nλiˉTi)=i=1∑n∣λi∣2Ti=i=1∑nTi=I
이때 정규연산자이므로 T2=T이고, 다른 고유값에 대응하는 연산자와 직교한다는 사실을 명심하자.
위의 결과로도 T가 유니타리 연산자임을 확인할 수 있다.
따름정리 3
F=C일 때, T가 자기수반연산자이기 위한 필요충분조건은 T가 정규연산자이고, T의 모든 고유값이 실수인 것이다.
증명
T가 정규연산자이고 모든 고유값이 실수라 가정해보자. T의 스펙트럼 분해를 T=∑i=1nλiTi라 하면, 다음이 성립할 것이다.
T∗=i=1∑nλiˉTi=i=1∑nλiTi=T
그러므로 T는 자기수반 연산자이다.
역으로 T가 자기수반연산자라 가정하면, 자연스레 T는 정규연산자일 것이다. 또한, 이때 자기수반연산자의 성질에 의해 T의 고유값은 모두 실수일 것이다.
따름정리 4
T의 스펙트럼 분해가 T=∑i=1nλiTi이면, 각 Tj는 T에 대한 다항식이다.
증명
gj(λi)=δij(1≤j≤k)가 되도록 다항식 gj를 잡아보자. 이때 다음과 같은 식이 성립할 것이다.
gj(T)=i=1∑ngj(λi)Ti=i=1∑nδijTi=Tj