1. 일차 종속과 일차 독립
앞에서 span에 대해 다루었다. 그렇다면 아래와 같은 상황을 생각해보자.
벡터 에 대해, 집합 가 생성한 의 부분 공간을 라고 하자. 혹시 W를 생성할 수 있는 S의 진부분집합이 존재하지 않을까? 즉, S의 일부로 S의 전체를 span할 수 있지 않을까? 이는 결국 S의 한 벡터가 S에서 꺼낸 다른 벡터들의 선형결합으로 표현되는지 묻는 것이다.
이에 대해 스칼라 에 대해 다음과 같은 식으로 표현되는지 묻는 것과 같다.
다시 표현해보면 다음과 같다.
결국 꼴로 표현할 수 있고, 여기서 해당 연립방정식의 해가 존재하는지 묻는 문제라고 할 수 있다. 해가 존재한다면 위 선형결합이 성립할 것이다. 하지만 위의 선형결합은 성립하지 않는다. 위 방정식의 해가 존재하지 않기 때문이다.
하지만 아래 선형 결합식은 성립한다.
벡터 는 다른 세 벡터의 선형결합으로 표현될 수 있다. 하지만 이것이 "S의 어떤 벡터가 S의 다른 벡터들의 일차결합으로 표현될 수 있다."는 명제를 검증할 수는 없다. 이를 위해선 모든 벡터에 대해 검증해야 한다. 번거롭고 효율적이지 못할 수밖에 없다.
이를 다르게 생각해보자. 위의 식을 조금 변형시켜서
즉, S의 어떤 벡터가 다른 벡터의 선형결합으로 표현될 수 있다면, 영벡터를 S의 벡터들의 일차결합으로 표현할 때, 어떤 계수가 0이 아니다.
즉, 위의 행렬을 통한 방정식의 표현을 빌리면 이 성립한다면 해당 공간 S의 어떤 벡터는 다른 벡터의 선형 결합으로 표현가능하다. 여기서 한가지 정의가 나타난다.
만약 벡터 공간 V의 부분집합 S에 대해 Ax = 0을 만족하는 유한개의 벡터 와 적어도 하나가 아닌 0이 아닌 스칼라 이 존재하면, 집합 S는 일차종속이며, S의 벡터 또한 일차종속이다.
임의의 벡터 에 대해 이면, 이다. 이를 의 일차결합에 대한 영벡터의 자명한 표현이라 한다.
다시말해, 어떤 집합이 일차 종속이라면 해당 집합에 속하는 벡터들을 이용해 영벡터를 자명하지 않은 표현으로 표현할 수 있다.
벡터 공간의 부분집합 S가 일차종속이 아니라면 일차독립이다
일차 독립은 매우 중요한 개념이다. 우리가 일차 독립인 벡터를 이용해 공간을 span할 수 있다면, 매우 효과적으로 span할 수 있고, 계산량이 줄기 때문이다. 이는 모델의 크기가 작아진다는 것을 의미할 수 있다.
일차 독립인 집합에 대해 다음 명제는 모든 벡터 공간에서 참이다.
- 공집합은 일차독립이다. 어떤 집합이 일차종속이기 위해선 반드시 공집합이 아니어야 한다.
- 영이 아닌 벡터 하나로 이루어진 집합은 일차독립이다.
증명: 만약 영벡터가 아닌 가 일차 종속이라면 0이 아닌 스칼라 a에 대해 이다. 양변에 을 곱하면 이므로, u가 영벡터가 아니라는 사실이 모순이 되어버린다. - 어떤 집합이 선형독립이기 위한 필요충분조건은 0을 주어진 집합에 대한 일차겹합으로 표현하는 방법이 자명한 표현뿐인 것이다. 즉, 에 대해 이 유일한 해여야 한다.
이를 정리해서 유용한 결론을 얻어보자.
우리는 벡터공간 에서 진부분집합 를 통해 를 span하고자 한다. 이때, 진부분집합 가 정말로 span하기 위한 최소한의 벡터만 가지고 있는지 확인하는 것은 가 선형종속인지 확인하여 알 수 있다. 의 선형독립은 를 span하는 최소생성집합이기 위한 필요조건이다.
2. 기저와 차원
앞의 내용을 종합해보자. 결국 벡터 공간 의 부분집합이면서 를 span할 수 있는 최소생성집합 를 찾고자 지금까지 내용들을 다뤄왔다. 이를 기저라고 한다.
기저에 대한 정의는 다음과 같다.
벡터공간 와 부분집합 를 생각하자. 가 선형독립이고, 를 span하면, 를 의 기저(basis)라 한다. 가 의 기저일때, 의 벡터는 의 기저를 형성한다.
주의 할 것은 기저가 항상 유일하지 않다는 점이다. 공간에 대한 기저는 도 있지만, 도 있다.
이제 우리가 원하는 문장을 쓸 수 있게 되었다.
벡터 공간과 와 의 부분집합 가 있을 때, 임의의 벡터 를 에 속한 벡터의 선형 결합으로 나타낼 수 있고, 그 표현은 유일하다면 부분집합 는 벡터 공간 의 기저이기 위한 필요충분조건을 충족한다.
여기서 중요한 정리가 나오고, 이 정리에서 차원(dimension)이 도출된다. 집중해보도록 하자.
2-1. 대체 정리(Replacement Theroem)
n개의 벡터로 이루어진 집합 가 벡터공간 를 span할 때, 이 m개의 선형독립인 벡터로 이루어진 의 부분집합이면, 이다. 또한, 다음 조건을 만족하는 집합 가 존재한다. 는 n - m개의 벡터로 이루어져 있으며, 는 를 span한다.
즉, 벡터공간 를 span하는 부분집합은 기저와 동일한 벡터 수를 가지거나 많고, 벡터공간 를 span하는데 필요한 최소 벡터의 수가 정해져있다.
증명해보자.
m에 대해 수학적 귀납법으로 증명할 것이다.
1. m = 0 이라면 H = G가 되면 성립하게 된다.
2. 이 m + 1개의 벡터로 이루어진 선형독립인 부분집합이라 하자. 가 벡터공간일때, 이라면 이 선형독립이면, 역시 선형독립이기 때문에, 선형독립이다.
가정에 의해 집합 이 를 span하도록 하는 의 부분집합 이 존재하게 된다.(단, ) 이제 다음 등식을 만족하는 스칼라 과 스칼라 이 존재한다.
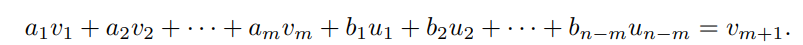
여기서 잠시 정리하고 넘어가자. 이때, 임을 유념하자. 만약 n = m이라면 은 의 선형결합이고, 이는 가정을 위반하게 된다. 그러므로 이다.
또한, b 중 0이 아닌 스칼라가 반드시 존재한다. 그렇지 않으면 방금 언급한대로 가정을 위반하게 된다. 이 스칼라를 이라 하자. 이때 식을 에 대해 풀면 다음과 같다.
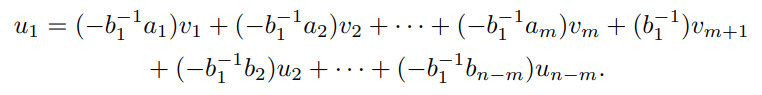
이때 이라 하면, 임을 알 수 있다. 이므로 다음이 성립하게 된다.
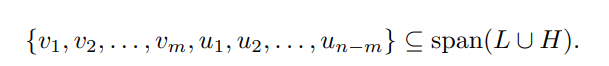
이때 가정에 의해 이 를 span하기 때문에 최종적으로 가 된다.
- 이때 H는 개의 벡터를 가진 의 부분집합이므로, 이 정리는 일 때도 성립한다.
증명은 여기서 끝이 난다.
그런데 이 대체정리에 따름정리가 존재한다.
벡터공간 가 유한집합인 기저를 포함한다고 가정하자. 의 모든 기저는 유한집합이며, 같은 개수의 벡터로 이루어져 있다.
증명은 위의 대체정리를 이용하면 간단하다.
n개의 벡터로 이루어진 벡터공간 에 를 기저로 가지면서 라는 기저가 n개를 초과하는 벡터로 이루어져 있다고 하자. 이때, 의 부분집합 중에 n + 1개의 벡터로 이루어진 부분집합 를 생각할 수 있다.
는 선형독립이고, 는 를 span하기 때문에, 대체정리에 의해 이 성립해야 한다. 하지만 이는 모순이므로, 가 m개의 벡터로 이루어진 유한집합이면 이 된다. 또한, 와 를 바꿔서 생각하면 이어야 하므로, 이어야 한다.
이를 조금 생각해보면 결국 유한집합의 기저를 가지는 벡터공간은 결국 그 벡터공간에 따라 정해진 갯수의 벡터로 이루어진 기저를 가지게 됨을 알 수 있다. 즉, 기저를 형성하는 벡터의 갯수는 벡터공간 의 본질적인 성질이다. 여기서 차원의 개념이 등장하게 된다.
기저가 유한집합인 벡터공간을 유한차원이라 한다. 또한, 의 기저가 n개의 벡터로 이루어질 때, 유일한 자연수 n은 주어진 벡터공간의 차원(dimension)이고 로 표시한다. 만약 벡터공간이 유한 차원이 아니라면, 무한차원이다.
결국 차원이란 벡터공간의 기저를 이루는 벡터의 갯수를 의미한다는 것을 알게되었다.
여기서 조금만 더 나아가서 대체정리를 생각해보자. 대체 정리를 증명하면서, 이라는 점을 한번 짚고 넘어갔다. 즉, 유한차원 벡터 공간 에서 보다 더 많은 갯수의 벡터를 가지는 부분집합은 절대로 선형독립일 수 없는 것이다.
