1. 행렬표현
유한차원 벡터공간 V의 순서기저는 순서가 주어진 기저를 의미한다. 즉, 기저벡터들이 유한수열의 형태로 주어지는 것을 순서기저라고 한다. 이를 이용하면 이제 좌표벡터를 우리는 표현할 수 있다.
정의 1. 유한차원 벡터공간 V의 순서기저를 β={u1,u2,…,un}이라 하고, x∈V에 대해 a1,a2,…,an은 x=∑i=1naiuu를 만족하는 유일한 스칼라라고 할 때, β에 대한 x의 좌표벡터는 다음과 같다.
[x]β=⎝⎜⎜⎜⎛a1a2…an⎠⎟⎟⎟⎞
다르게 이야기하면, x∈V에 대해 V의 순서 기저 β의 선형 결합으로 x를 만들때, 선형 결합의 계수가 좌표벡터 [x]β인 것이다.
이제 선형변환이 어떻게 행렬표현이 될 수 있는지 생각해보자. 유한차원 벡터공간 V,W와 각각의 순서기저 β={v1,v2,…,vn},γ={w1,w2,…wm}, 선형변환 T:V→W를 생각해보자. 이때, j=1,2,…,n일 때, j마다 다음을 만족하는 유일한 스칼라 aij∈F가 존재한다.
T(vj)=i=1∑maijwi
정의 2. 위의 상황에서 성분이 Aij=aij인 m×n 행렬 A를 순서기저 β와 γ에 대한 선형변환 T의 행렬표현이라 하고, A=[T]βγ라 표기한다. 이때, V=W,β=γ이면, 간단하게, A=[T]β라 표기하자.
즉, 행렬을 이용한 선형 변환이란 하나의 공간에 위치한 벡터를 다른 공간으로 선형 변환하여 나타내는 과정을 의미한다.
이때 영변환의 행렬표현은 영행렬이 되고, 항등변환의 행렬표현은 n×n인 In 항등행렬이 된다. 이제 행렬과 선형변환이 서로 연결되어 있음을 알 수 있다. 이때, 이 연결은 합과 스칼라곱을 보존한다.
정리 1. 즉, F-벡터공간 V,W와 선형변환 T,U:V→W에 대하여 다음이 성립한다.
1. 임의의 a∈F에 대하여 aT+U는 선형이다.
2. 선형변환의 합과 스칼라 곱을 정의할 때, V에서 W로 가는 모든 선형변환의 집합은 F-벡터공간이다.
위의 두번째 성질에서 다음과 같은 정의가 도출된다.
정의 3. F벡터공간 V,W에 대하여 V에서 W로 가는 모든 선형변환의 모임으로 이루어진 벡터공간을 L(V,W)라 표기한다. 이때, V=W라면 간단히 L(V)로 표기한다.
2. 선형변환의 합성과 행렬 곱
앞서 집합 L(V,W)가 벡터 공간의 공리를 만족하기 때문에, 선형변환의 합이 행렬의 합으로 표현될 수 있을 것이다. 그렇다면, 선형변환의 합성은 행렬로 표현하면 어떻게 될까? 행렬 곱으로 표현할 수 있다.
F-벡터공간 V,W,Z와 선형변환 T:V→W,U:W→Z를 생각하자. 두 선형변환의 합성 UT:V→Z는 선형변환이다.
즉, 선형 변환의 합성은 다시 선형변환이라는 것인데, 다음을 통해 확인할 수 있다.
UT(ax+y)=U(T(ax+y))=U(aT(x)+T(y))=U(aT(x)+U(T(y))=aU(T(x))+U(T(y))=aUT(x)+UT(y)
이제 선형변환의 합성이 선형변환임을 알았으니, 이를 어떻게 행렬곱이라 할 수 있는지 살펴보도록하자.
유한차원 벡터공간 V,W,Z와 선형변환 T:V→W,U:W→Z가 있다. V의 순서 기저 α={v1,…,vn}, W의 순서기저 β={w1,…,wm}, Z의 순서기저 γ={z1,…,zp}에 대하여, A=[U]βγ,B=[T]αβ라 하자. 이때, AB=[UT]αγ가 되는 행렬곱을 정의해보자. 이때 UT(vj)는 다음과 같이 자연스레 변환될 수 있을 것이다.
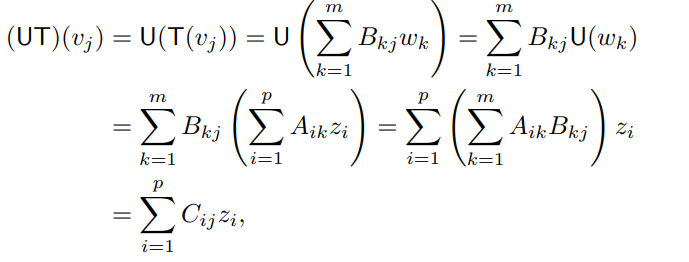
이때, Cij=∑i=1mAikBkj이므로, 행렬곱은 다음과 같이 정의가 가능해집니다.
정의 : m×n 행렬 A와 n×p 행렬 B에 대하여 두 행렬 A,B의 곱AB는 다음과 같이 정의된 m×p 행렬이다.
1≤i≤m,1≤j≤p에 대하여 (AB)ij=∑k=1nAikBkj
쉽게 표현하면 (AB)ij는 A의 i행과 B의 j열을 내적한 것이다.
이때, 행렬 곱에 대해 결합법칙은 성립하나, 교환법칙은 성립하지 않으며, 행렬곱의 전치는 위치가 바뀐다. 즉, (AB)T=BTAT이다.
행렬의 성징은 다음과 같다.
A 가 m×n 행렬, B와 C가 n×p 행렬, D와 E가 q×m 행렬일때,
- A(B+C)=AB+AB,(D+E)A=(DA+EA)
- 임의의 스칼라 a에 대하여, a(AB)=(aA)B=A(aB)
- ImA=A=AIm
행렬을 선형변환으로 볼 때, 일반적으로 행렬을 좌측에, 변환할 벡터를 오른쪽에 놓게 된다. 만약 행렬이 U:V→W에서 A=[U]αβ라면, Ax이고, x∈V여야 행렬 A가 선형변환 U에 대응되기 때문이다. 이를 좌측 곱 변환이라 하며 다음과 같이 정의할 수 있다.
정의 :A는 m×n행렬이고, 성분은 체 F의 원소이다. 다음 선형변환을 간단히 LA라고 표기하자.
LA:Fm→Fn,LA(x)=Ax
이때, LA는 좌측 곱 변환(left multiplication transformation)이라 한다. 이때, x는 Fn의 열벡터이고, Ax는 A와 x의 행렬곱이다.