이전까지 선형이 무엇인지, 선형변환이 어떻게 행렬과 이어지는지 공부했다. 이제 행렬에 대해 본격적으로 다루기에 앞서 다양한 행렬의 성질과 연산을 배워보자.

1. 기본행렬연산

$m \times n$ 행렬 $aA$에 대하여 $A$의 행에 대한 다음 세 연산을 기본행연산(elementary row operation)이라 한다. 또한 그 표기법 역시 보이자.

1. $A$의 두 행 i와 j를 교환하는 것 : $A_i\leftrightarrow A_j$
2. $A$의 한 행 i에 0이 아닌 스칼라 a를 곱하는 것 : $aA_i \to A_i$
3. $A$의 한 행 i에 다른 행 j의 스칼라 a배를 더하는 것 : $A_i + aA_j \to A_i$

위의 세 연산을 기본연산(elementary operation)이라 하며, 각 연산을 1형, 2형, 3형이라 한다.

이때 한가지 염두에 둘 것은 $A$ 행렬에 기본연산을 통해 $B$ 행렬을 만들었다면, 역으로 $B$ 행렬에 기본연산을 통해 $A$ 행렬을 만들 수 있다는 점이다. 또한, 기본행렬을 정의할 수 있다.

정의 1: $n\times n$ 기본행렬은 항등행렬 $I_n$에 기본연산을 적용하여 얻은 행렬이다. 이때, $I_n$에 1형, 2형, 3형 연산을 하여 얻은 행렬을 각각 1형, 2형, 3형이라 한다.

다른 말로 하면, 기본행렬에 기본 연산을 가하면 항등행렬을 만들 수 있다.

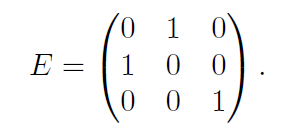
예를 들어 위의 기본 행렬 E에 1형 연산($E_1 \leftrightarrow E_2$)을 가하면 항등행렬이 된다.

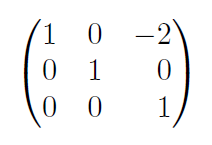
혹은 위의 기본행렬 E에 3형 연산($E_1 + 2E_3 \to E_1$)을 가하면 항등행렬이 된다.

그런데 어떠한 행렬에 기본행연산을 가하는 것은 그 행렬에 대응하는 기본행렬을 곱하는 것과 동일하다.

정리 1: 행렬 $A \in M_{m \times n}(F)$에 기본 행(열)연산을 하여 행렬 $B$를 얻었다면, $B = EA(B = AE)$가 되는 $m\times m (n\times n)$ 기본행렬 $E$가 존재한다. 혹은 $A$에서 $B$를 얻은 기본행(열)연산을 $I_m(I_n)$에 똑같이 적용하면 $E$가 된다.

즉, $E$가 $m\times m(n\times n)$기본행렬일 때, $I_m(I_n)$에서 $E$를 얻은 기본행(열)연산을 $A$에 똑같이 적용하면 $EA(AE)$가 된다.

즉 우리가 행렬 $A$를 일정한 기본 연산을 통해 행렬 $B$로 바꾸고 싶다면 각 기본연산의 역원을 $I_n(I_m)$에 가하여 $E$를 구하고, $E$를 $A$와 행렬곱하여 $B$를 구할 수 있다.

이때 유용한 특성 중 하나가 다음과 같은 정리이다.

정리 2. 기본행렬은 가역이다. 즉, 역행렬이 존재한다. 그 역행렬은 같은 종류의 기본행렬이다.

가역성에 대해서는 역행렬을 다루면서 좀 더 살펴보기로 하고, 중요한 것은 우리는 어떠한 기본행렬이든 구할 수 있다는 점이다.