A Short Introduction to Adaboost

Relation to Support-Vector Machines

이 장에선 SVM과 Adaboost의 관계에 대해 다루고 있습니다. 결론부터 이야기하면, "서로 다른 듯 보이지만 Adaboost는 SVM의 장점을 가져오고자 했다." 입니다. 여기서 장점이란 과적합에 강건하다는 점입니다. 이 점을 염두에 두고 시작하겠습니다.

margin theory에선 부스팅 모델들과 SVM의 공통점을 알 수 있습니다. 여기선 부스팅 모델이 약한 분류기를 이미 찾았고, 각각의 분류기를 엮어서 강한 분류기를 만들 때 필요한 $\alpha$를 찾는 단계라고 생각해봅시다.

합리적으로 생각해보면, 부스팅 모델이 일반화가 잘 될 수 있도록 $\alpha$를 선택해야 할 것 입니다. 이를 위해 앞에서 언급한 식인

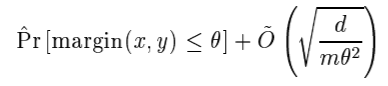
을 최소화하면 될 것입니다. 이 식이 나타내는게 부스팅 모델의 일반화 성능의 최대값이니까요(maximum error bound).

여기서 식이 너무 복잡하니까, 앞의 항은 0이라고 간주합시다. 즉, 모델이 예측한 레이블이 모두 정확하다고 간주하는 겁니다(과적합 상황 가정). 뒷 항은 분류기의 margin에 대한 항이므로 이제 SVM처럼 각 데이터 중 margin이 가장 작은 데이터의 margin을 최대화하는 문제가 됩니다.

여기서
$h(x) = <h_1(x), h_2(x), ... , h_N(x)>$
$\alpha =<\alpha_1 , \alpha_2, ..., \alpha_N>$
이런 식으로 벡터화하여 표현하겠습니다.

$h(x)$는 각 약한 분류기의 예측값이 될 것이고, $\alpha$는 각 약한 분류기의 예측값에 대한 가중치가 될 것입니다.

위에서 확인했던 margin에 대한 식과, 여기서 정의한 두 벡터를 이용하면 margin은 다음과 같이 표현할 수 있습니다.

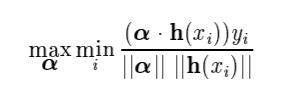
이 식을 해석해보면, margin이 제일 작은 데이터(row, instance)의 margin을 최대화 하는 $\alpha$를 찾는 것입니다.
그리고 여기서 l1 norm은 각 원소의 절대값의 합이고, lmax norm은 각 원소 중 최대값이므로 다음과 같은 식으로 표현할 수 있습니다.

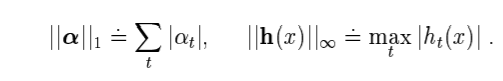
그런데 $h_t(x)$는 -1 혹은 1의 값을 반환하는 함수이므로 $\lVert {h(x)}_{\infin}\rVert = 1$일 것입니다.

하지만 SVM은 다음과 같은 식을 사용하여 각 벡터를 정의합니다.

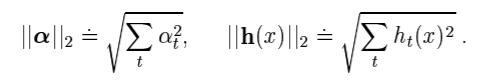
부스팅 모델과 다른 점은 두 항 모두 l2 norm을 이용하여 유클리드 거리를 사용한다는 점입니다.

부스팅 모델을 SVM처럼 보면, 이렇게 사용하는 norm의 차이 외에는 큰 차이가 없는 것으로 보입니다. 하지만 이 작은 차이로 인해 다음과 같은 3가지의 큰 차이점이 발생합니다.

1. 다른 norm의 사용 = margin의 큰 차이
   차원 수가 크지 않을 때, norm의 차이는 사실 크지 않습니다. 2차원에 l1 norm을 사용하나 l2 norm을 사용하나 대각선과 직선 정도의 차이를 가져올 뿐입니다. 하지만 차원이 커질 수록 norm에 따른 차이는 급격히 커지게 됩니다.
   예를 들어, 1x1 짜리 정사각형을 상상해봅시다. l1 norm을 사용할 경우 2지만 l2 norm을 사용하면 $\sqrt{2}$로 그 차이는 $2 - \sqrt{2}$ 입니다. 하지만 1x1x1 짜리 정육면체에선 l1 norm 은 3, l2 norm은 $\sqrt{3}$으로 두 차이는 $3 - \sqrt{3}$으로 2차원에서보다 커지게 됩니다.
   부스팅 모델이든 SVM이든 데이터의 차원수는 큰 것이 일반적인 경우입니다. 특히, 변수 간의 관계가 높을수록, 즉 $\alpha$가 매우 sparse한 벡터일 경우 이 문제는 커지게 됩니다. (변수 간 관계가 높다면 하나의 변수가 다른 변수의 많은 부분을 설명하기 때문에 $\alpha$가 대부분 작은 값을 가지는 벡터가 됩니다.) 이 경우 $l_{max}$ norm(부스팅)에선 단순히 큰 값을 취하면 되지만 l2 norm(SVM)에선 모든 원소를 제곱합하게 됩니다. 차원수가 많다면 두 norm 사이의 차이는 커질 수 밖에 없습니다.

2. 컴퓨터 연산량 차이
   SVM은 기본적으로 연산량을 많이 필요로 합니다. 커널에 따라 다르지만 보통 $O(N^2)$ 혹은 $O(N^3)$의 연산량을 필요로 합니다. 하지만 부스팅 모델은 (우리가 사용하는 한) 기본적인 트리 모델을 사용하기 때문에 $O(N)$으로 훨씬 적은 연산량을 가지고 있습니다. 맞아요 논문에서 자기들이 잘했다고 자랑하는 겁니다.

3. 고차원 데이터 사용
   SVM과 부스팅 모델은 고차원 데이터를 효율적으로 사용하기 위해 다루는 탐색 방식이 다릅니다.
   SVM은 고차원 데이터를 커널을 이용해 저차원으로 맵핑하여 문제를 해결하지만, 부스팅은 greedy search(탐욕 알고리즘)을 이용하여 문제를 해결합니다. 탐욕 알고리즘이란 최종적인 결과를 고려하지 않고(보통 최종 결과를 고려할 수 없을 때 사용합니다.) 현재 상황에서 최선의 결과를 선택하는 것을 의미합니다. adaboost는 이전의 학습기가 제대로 예측하지 못한 오류만 고려하므로 탐욕 알고리즘을 채택했다고 볼 수 있습니다.

Multiclass Classification

이전까지 이진 분류 문제를 가정하여 adaboost를 설명했습니다. 그렇다면 다중 분류 문제에선 adaboost를 어떻게 적용할 수 있을까요. 앞으로 몇가지 방법을 소개하도록 하겠습니다.

1. AdaBoost.MH
   이 모델은 n개 클래스에 대한 다중 분류 문제를 n개의 이진 분류 문제로 전환하여 해결합니다. 예를 들어 개, 고양이, 사자, 호랑이에 대한 분류 문제가 있다면, MH 모델은
   (1) 개인가 다른 동물인가
   (2) 고양이인가 다른 동물인가
   (3) 사자인가 다른 동물인가
   (4) 호랑이인가 다른 동물인가
   의 문제로 전환하여 문제를 해결합니다.

2. AdaBoost.M2
   이 모델은 MH 모델에 비해 조금 복잡하게 문제를 해결합니다. 위의 예시를 이용해보자면
   (1) 개인가, 고양이인가
   (2) 개인가, 사자인가
   (3) 개인가, 호랑이인가
   (4) 고양이인가, 사자인가
   (5) 사자인가, 호랑이인가
   (6) 사자인가, 호랑이인가
   의 문제로 변환합니다.

이렇게 각각의 이진분류문제로 전환하여 예측값을 산출하면 MH 모델은 4개, M2 모델은 6개의 예측값이 나오는데 이것들을 어떻게 합칠까요?
가장 단순한 방법은 voting, 즉 다수결을 통해 해결합니다.
혹은, margin 계산하기. 각 이진분류문제마다 margin을 계산할 수 있습니다. 이 margin을 이용하여 가장 margin이 먼 클래스로 분류하면 됩니다.

Experiments and Applications

Adaboost는 빠르고, 단순하며, 코딩하기도 쉽습니다. 크게 보면 round 수를 제외하면 튜닝해야할 파라미터도 없습니다. 심지어 약한 분류기를 어떻게 합쳐야 할지 고민할 필요도 없죠. 즉, 충분한 데이터와 충분한 약한 분류기를 확보할 수 있다면 최소한의 성능을 확보할 수 있는 모델입니다. 전체 변수, 전체 데이터를 잘 맞추는 모델을 만들 필요 없이 50% 이상의 정확도를 가지는 약한 학습기만 만들면 되니까요.

반대로 말하면, 데이터가 충분하지 못하거나, 학습기의 성능을 50%이상 확보하지 못하면, 절대로 제대로 학습하지 못하는 모델입니다. (현재 상황에서 생각하면 사실 고려할 필요도 없을 정도의 문제점이죠) 하지만 이외에도 단순한 트리 기반 + 탐욕 알고리즘의 조합으로 인해 노이즈에 예민하다는 문제점도 존재합니다.

그러면 실험은 어떻게 되었나 살펴보도록 합시다.

1. UCI benchmark Dataset + C4.5
   UCI 데이터셋은 UC 어바인 대학교에서 제공하는 머신러닝을 위한 다양한 데이터셋입니다. 이 논문에선 각각의 데이터셋에 대해 적용하여 결과를 살펴보았습니다.
   사용한 모델은 C4.5라는 트리 모델과 단순히 하나의 가지만 치는 stump 모델이었습니다. C4.5 모델은 가지치기(prunning)이 제공되는 트리 모델입니다. 그 결과는 다음과 같습니다.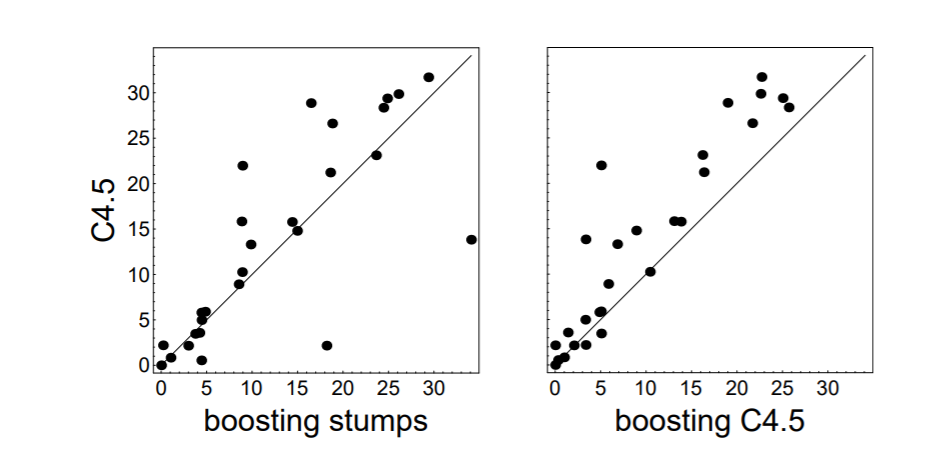
   y 축은 C4.5 모델만 사용한 것이고, x 축은 stump나 C4.5 모델을 부스팅한 결과입니다. 정확도를 scatter plot으로 나타낸 것이기 때문에, 부스팅을 사용하였을 때, 대부분의 경우에 C4.5보다 좋은 성능을 보이는 것을 알 수 있습니다.

2. Text Cateogorization
   자연어 처리에서 학습 시 사용되지 않은 단어나 문장이 테스트 시 나타나는 것은 큰 문제입니다(보통 Out of Bag, OOB 문제라고 합니다). 이를 고려하여 문서 분류 문제에선 테스트 시의 성능을 평가하였습니다. 결과는 아래와 같습니다.

그 결과 AdaBoost의 성능이 다른 어떤 모델보다 항상 좋은 것을 알 수 있습니다. 부스팅 방법론은 이외에도 문서 필터링(스팸 처리), 랭킹 시스템(추천), 분류 문제에서 광범위하게 사용되고 있다고 합니다.

3. 이상치 식별(identification of outlier)
   Adaboost의 장점 중 하나는 이상치를 식별한다는 것입니다. 우리가 흔히 사용하는 이상치 탐지가 아니라 식별한다고 번역한 것은 이상치(클래스가 잘못 분류되어 있거나, 데이터가 분류하기에 모호한 데이터일 경우)를 의미합니다. Adaboost는 round를 거듭하면서 분류하기 데이터에 집중하기 때문에
   가중치가 큰 데이터는 종종 이상치일 수 있습니다. 다음을 살펴봅시다.
   
   위 데이터는 각각 round가 4, 12, 25일 때 큰 웨이트를 가지고 있는 데이터입니다. 그림 밑에 써져 있는 숫자는 $d:l_1/w_1, l_2/w_2$ 입니다. d는 실제 클래스, $l_n$은 n번째로 높은 weight를 가진 클래스 $weight_n$은 해당 웨이트 입니다. 각각의 데이터들은 $w_1$과 $w_2$가 거의 동일한 것을 볼 수 있는데요. Adaboost에서 이를 분류하기 힘들어하는 것을 의미합니다.

이렇게 이상치에 민감하게 반응하다 보니, 이상치의 개수가 Adaboost의 성능에 큰 영향을 미치게 됩니다. 이를 해결하기 위해 이상치에 적은 가중치를 부여하는 Gentle AdaBoost가 제시되었다고 합니다!