1. Introduction

어느 딥러닝 분야가 그렇지 않겠냐만, 강화학습 분야에서 고차원 input을 이용하여 agent를 컨트롤하는 것은 오래된 숙원이었다. 이 논문 이전에 대부분의 강화학습 방법론은 임의로 정의된 선형 함수를 이용하거나 정책을 이용하여 고차원 데이터에 대응해왔다.

하지만 딥러닝이 발달하면서 고차원의 데이터에서 feature extraction이 가능해지기 시작했다. 휴리스틱한 임의의 함수를 정의할 필요없이, 딥러닝 모델을 이용해 feature map 혹은 embedding vector를 생성할 수 있게 된 것이다.

이는 CNN, RNN, 제한 볼츠만 머신 등을 지도학습, 비지도학습 방법론 등에 적용하여 가능하다. 강화학습을 연구하는 저자는 자연스레 이러한 feature extraction을 강화학습에 적용해보고자 했다.

하지만 기존의 딥러닝 방법론과 강화학습 방법론은 분명히 다른 점이 존재하고, 이는 feature extraction을 강화학습에 이식하는데 어려움으로 작용했다고 한다. 어려움을 정리해보면 다음과 같다.

1. 딥러닝 기법은 대부분 대량의 레이블이 있는 데이터를 이용해 학습한다. 하지만 강화학습은 그렇지 못하다. 강화학습 알고리즘은 보통 scalar 값인 리워드를 이용해 sparse하고 noise도 많고, 곧바로 적용되지 않는(delayed) 학습을 수행한다. 이 행동과 이에 수반되는 리워드 사이의 시간적 간극은 엄청 길 수도 있다(수 천 time step 만큼).
2. 딥러닝 기법은 각 instance가 독립이라고 간주한다. 즉, 이전의 학습에 사용된 instance와 현재의 instance가 전혀 연관이 없는 것이다. RNN류 모델에서도 time step 별로 instance를 전처리하여 생성하기 때문에 이 가정을 만족한다. 하지만 강화학습은 그렇지 못하다. 에이전트는 행동하고 환경이 변화하고 다시 변화한 환경에서 행동을 정해야 한다. 즉, instance 간에 상관 관계가 높다.
3. 아마 이게 가장 중요하지 않을까 싶은데, 강화학습에선 에이전트가 행동하고 결과를 학습하면서 데이터 분포가 지속적으로 변화한다. 딥러닝에서 데이터 분포는 절대 변할 리 없기 때문에 큰 차이점이다. (딥러닝에선 학습 데이터를 학습 중에 건들이지 않는다.)

이 논문은 CNN을 이용하여 비디오 데이터에서 성공적으로 정책을 학습했다고 한다. 특히, Q-learning 알고리즘을 사용하였다고 한다. 위에서 제시한 상관관계가 높은 데이터와 지속적으로 변화하는 데이터 분포 문제는 experience replay 메커니즘을 사용하여 극복하였다고 한다. experience replay 메커니즘이란 이전의 transition을 무작위 샘플링하여 학습 분포를 지속적으로 smoothing 해주는 것이라고 한다.

논문에선 실험을 위해 아타리 2600의 게임들을 활용했다고 한다. 아타리 2600 게임들은 210x160 RGB 이미지가 60Hz로 제공되기 때문에 매우 고차원의 입력데이터가 되어 강화학습에서 해결하기 어려운 태스크라고 한다.

논문 저자들은 정말 순수하게 신경망 에이전트만 이용하여 게임을 하게 만들고 싶었던 것 같다. 사전 규칙이나, 에뮬레이터의 정보, 휴리스틱하게 가공한 정보없이 정말 사람처럼 이미지만 이용해 에이전트를 학습시켰다. 게다가 게임마다 하이퍼 파라미터나 모델 구조를 변경하지 않았다고 하니, 목표가 높았다... 그 결과를 미리 말하자면 이전의 강화학습 알고리즘에 비해 전체 7개 게임 중 6개가 월등한 성능을 보였고, 심지어 3개의 게임에선 게임을 잘하는 사람보다도 월등했다고 한다.

2. Background

용어 정리

• 에이전트가 상호작용하는 환경 : $\epsilon$
• time step t마다 에이전트가 선택한 행동 : $a_t$
• 에이전트가 선택할 수 있는 행동 : $A = \{1, ..., K\}$
• 에뮬레이터가 출력하는 이미지 : $x_t\in \mathbb{R^d}$
• 게임 상태 변화에 따른 리워드 : $r_t$
• 현재 상태 : $s_t$

에이전트가 수행한 행동 $a_t$는 에뮬레이터에 입력되어 에뮬레이터 내부의 상태를 변화하게 하고, 점수를 조정한다. 하지만 에이전트는 에뮬레이터 내부를 볼 수 없기 때문에 관찰 할 수 있는 것은 오직 이미지 $x_t$ 뿐이다. 또한, 게임 점수가 변화함에 따라 얻는 $r_t$는 사실 하나의 행동이 아닌 이전의 수많은 행동의 연속적인 실행으로 얻어진다.

에이전트는 에뮬레이터가 현재 출력하는 이미지만 입력받을 수 있다. 즉, 에이전트가 현재 입력 데이터로 얻을 수 있는 정보가 매우 제한적이다. 그러므로 $s_t$는 다음과 같이 과거 행동과 입력값의 집합으로 표현된다.
$s_t = x_1, a_1, x_2, a_2, x_3, a_3, ..., a_{t-1} , x_t$
여기서 $s_t$를 이용해 다음 행동을 정해야 하기 때문에 이전 행동인 $a_{t-1}$까지만 상태에 포함된 것에 유의하자.

모든 시점 t마다 사실 이전의 모든 행동과 입력값만 가지고 있으면 표현이 가능하다. 이는 $s_t$가 매우 크지만 유한한 값을 가지는 것을 의미하고, 즉, 마르코프 결정 프로세스를 사용할 수 있음을 의미한다. 결과적으로, 마르코프 결정 프로세스를 이용한 일반적인 강화학습이 가능해진다.

에이전트의 목표는 현재 상태를 고려하여 미래의 리워드를 최대화할 수 있는 행동을 에뮬레이터에 입력하는 것이다. 하지만 먼 미래의 보상은 불확실하고, 가까운 미래의 보상은 비교적 확실하다. 즉, 같은 100의 보상이라고 예측되더라도 가까운 보상이 훨씬 큰 값이다. 이를 고려하여 할인율 $\gamma$를 매 타임스텝마다 곱해주었다. 할인율을 고려한 t 시점의 보상은 다음과 같다.

• $t 시점의 보상(R_t) = \sum^T_{\acute{t} = t} \gamma^{\acute{t} - t}r_{\acute{t}}$

식이 어려워 보이지만 단순하다. 현재 시점보다 먼 보상은 작게, 가까운 보상은 크게 반영한다는 것이다.

행동가치함수는 특정 상태 $s$일 때, 특정 행동 $a$을 할 경우 기대되는 최대 보상 $R_t$를 반환하는 함수로, 다음과 같이 정의할 수 있다.

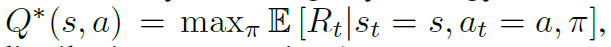
이때 $\pi$는 행동 분포라고 한다.

이때 행동-가치 함수는 벨만 방정식을 따르게 되는데, 벨만 방정식은 이번 시점에 가능한 모든 행동에 대해 알고 있을 때, 최적의 전략은 $r + \gamma Q(\acute{s}, \acute{a})$를 최대화하는 행동을 선택하는 것이다라고 정리할 수 있다.

수많은 강화학습 알고리즘들이 이 벨만 방벙식을 이용해 반복적으로 행동-가치 함수를 업데이트한다. 즉, t시점에서 벨만 방정식을 통해 t+2 시점의 최대화 행동을 선택하고 이를 통해 t+1 시점의 최대화 행동을 선택하는 식이다.

이러한 반복을 통해 무한히 큰 미래 시점을 고려하여 수렴하는 $Q$함수를 추정하게 되는 것이다.

하지만 이러한 방식은 실제로 적용이 가능하지 않다. 무한히 큰 미래 시점을 어떻게 고려할 수 있겠는가. 실제론 함수 추정자(approximator)를 이용한다. 일반적인 추정자는 선형 함수이지만, 신경망과 같은 비선형 함수 또한 사용이 가능하다. 논문 저자들은 추정자로서 신경망을 사용하여 Q-network를 구성하였다. Q-network는 로스 함수를 이용해 훈련될 수 있는데 로스 함수는 다음과 같이 정의된다.

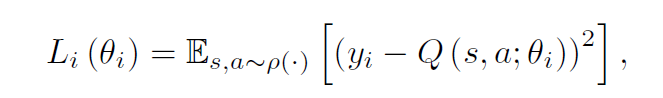
이때, $y_i$는 행동 확률 분포인 $\rho(s,a)$를 따르는 리워드 기대값이다.

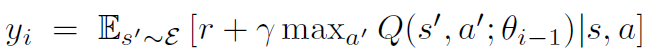
i-1 시점의 Q-network 파라미터인 $\theta_{i-1}$은 $L_i(\theta_i)$를 통해 업데이트 된다. 이때 $y_i$ 식 내부를 살펴보면 $\theta_{i-1}$이 있는 것을 알 수 있는데, 즉, 강화 학습의 신경망의 y값은 이전 시점의 신경망 파라미터의 영향을 받는다. 이 점이 지도학습의 신경망과 다른 점이다.

신경망 최적화기로는 SGD를 사용하였다. 즉, $\rho$를 따르는 하나의 instance에 대해 연속적으로 파라미터를 업데이트하는 과정을 모든 instance에 대해 전체 epoch만큼 반복하면, 비로소 Q-learning 알고리즘이 완성되는 것이다.

이렇게 만들어진 Q-learning은 두가지 특징이 있다.

• model-free: 이 알고리즘은 에뮬레이터에서 바로 샘플을 추출하여 사용한다. 에뮬레이터와 혹은 환경과 연동되지 않는다.
• off-policy: 이 알고리즘은 greedy startegy를 채용하였다. 이는 $\epsilon$의 확률로 랜덤한 행동을 하고, $1 - \epsilon$의 확률로 $a = max_a(Q(s,a;\theta)$인 행동을 한다. $a$는 신경망에 따라 추정된 리워드가 최대인 행동이다.

Related Work

논문에 따르면 가장 성공한 강화학습은 TD-gammon이다. backgammon 게임을 히든 레이어가 하나인 MLP를 이용한 가치 함수를 추정하여 자기 학습 및 강화 학습을 이용해 인간을 넘어서는 성능을 보였다고 한다.

그러나 TD-gammon의 방법론을 이용해 체스, 바둑, 체커스를 학습하려고 했던 시도들을 실패했다고 한다. 이는 해당 알고리즘이 backgammon 게임의 주사위 굴리기가 무작위성을 가지고 있어서 상태 공간을 탐색하는데에 특화되었기 때문으로 추정된다.

더군다나 비선형 함수나 off-policy learning를 이용한 Q-learning 강화학습 알고리즘들은 대체로 발산하는 것으로 알려져 대부분의 연구가 선형 함수를 이용했다고 한다.

논문이 쓰일 당시에는 강화학습에 딥러닝을 적용하려는 시도들이 여럿 있었던 것 같다. 강화 볼츠만 머신을 이용해 가치 함수나 정책 등을 학습하고자 했다. 또한 위에서 언급한 Q-learning의 발산 문제는 gradient temporal difference을 이용해 어느 정도 해결되었다고 한다(사실 어떤 것인지 잘 모른다... 기회가 되면 찾아보도록 하자). 하지만 이러한 시도들은 고정된 정책을 비선형 함수 추정자로 적용하거나 통제 정책(control policy)을 선형 추정자와 제한적인 파생 Q-learning으로 활용할 때 수렴한다고 증명된 것들이다. 아직 비선형 통제로는 확장되지 못했었다.

본 논문과 비슷한 연구로는 neural fitted Q-learning이 있다고 한다. NFQ는 위에서 언급한 로스 함수를 최적화하는데 RPROP 알고리즘을 사용한다. 하지만 배치 학습을 사용하여 컴퓨터 자원이 많이 필요하다는 한계가 있었다.
NFQ는 실제 이미지(real word)를 입력값으로 활용하기도 했다. 이때 오토인코더를 이용해 저차원으로 맵핑했다. 하지만 본 논문은 end to end 방법론으로 실제 입력값을 어떻게 하면 저차원에 맵핑시키는지 까지 학습하고 있다.

아타리 2600 게임을 강화학습에 이용한 것은 이미 다른 논문에서 소개된 적이 있다. 해당 논문에서는 일반적인 강화학습 알고리즘을 선형 추정자를 이용하여 게임을 학습하고자 했다. 그 결과 많은 양의 변수를 사용하고 tug of war 해싱을 이용해 변수들의 차원을 낮추어 성능을 향상시켰다. 또한, HyperNEAT이라는 아키텍처도 아타리 게임에 적용되었었습니다. 해당 아키텍처는 에뮬레이터의 리셋 기능을 이용하여 연속적으로 결정을 내리도록 학습되었는데, 각 몇몇 게임에서 디자인 결함을 이용하는 전략을 찾았습니다.

4. Deep Reinforcement Learning

컴퓨터 비전과 발화 인식 분야에서 대용량 데이터를 이용한 딥러닝 모델링이 큰 발전을 가져왔습니다. 그 중에서도 가장 큰 발전은 대용량의 raw data를 조금의 파라미터 업데이트(작은 람다 값)를 SGD를 이용해 수행하는 것을 발견한 것입니다. 특히나, 충분히 많은 데이터가 주어진다면 딥러닝은 휴리스틱하게 만들어낸 변수들보다 더 우수한 잠재 변수들을 raw data에서 추출해내는 것으로 알려져있습니다. 저자는 이러한 발견을 이용한 게임 실행 시 출력되는 RGB 값에서 딥러닝을 이용해 변수를 추출하고자 했습니다.

앞에서 이야기한 TD-Gammon은 이미 시행해본 미래 시점의 정책을 이용하여 가치 함수를 최적화했다고 합니다. 하지만 이런 방식은 매우 넓은 환경(enviroment)에서 효과적으로 작동할 리 없기 때문에 본 논문에선 다른 방법을 사용했습니다.

본 논문에선 expreience replay라는 기술을 활용했습니다. experience replay는 각각의 타임스텝 마다 $e_t = (s_t,a_t,r_t, s_{t+1})$로 정의된 경험을 랜덤하게 추출(여기서 SGD인 이유가 나타납니다.)합니다. 그리고 이 경험들은 $D = e_1, ..., e_N$으로 데이터셋으로 저장합니다. 그리고 이렇게 추출된 경험을 이용해 Q-learning을 업데이트합니다. Q-learning이 업데이트 되면, 에이전트는 $\epsilon$-greedy policy에 따라 행동을 선택하여 수행합니다. Q-learning 시 가변적인 길이를 가지는 input을 딥러닝 모델에 학습시키는 것은 무척 어렵기 때문에 $\phi$ 함수를 이용해 고정 길이 표상(representation)을 만들어 사용합니다.

이러한 방식은 기존의 Q-learning에 비해 몇가지 이점을 가집니다.

1. 각 경험 $\epsilon$는 랜덤하게 추출되어 반복적으로 파라미터 업데이트에 사용되므로 기존의 방법보다 데이터를 효율적으로 사용하게 됩니다.
2. 연속해서 샘플들을 사용할 경우 데이터 간에 상관관계가 높아서 효율적인 학습이 이루어지지 않습니다. 이를 $\epsilon$-greedy를 이용하여 학습 데이터 간 상관관계를 무너트렸기 때문에 훨씬 효율적으로 학습이 진행됩니다.
3. 안정적인 학습이 가능합니다. on-policy를 이용한 학습은 다음 데이터 샘플을 스스로 결정하기 때문에 편향이 발생할 수 있습니다. 예를 들어, 왼쪽으로 가는 것이 최적의 선택이라 판단한다면 이후 행동 분포는 이 선택에 모두 종속되게 됩니다. 이는 파라미터가 local minimum에 빠지거나 발산할 우려가 존재합니다. 하지만 본 논문은 experience replay를 이용해 이전의 학습 결과들을 smoothing하기 때문에 발산하거나 local minimum에 빠질 우려가 적습니다. 다시한번 강조하면, experience replay에선 행동 정책의 $\epsilon$과 추정자의 $\theta$가 다른 파라미터입니다.

여기서 전체 구조를 다시 짚고 넘어가면, 본 논문의 알고리즘은 직전 N개의 경험만 replay memory에 저장하고, 샘플들은 uniform distribution으로 $D$에서 추출됩니다. 이는 두가지 한계점을 가지고 있는데, 중요한 transition을 memory buffer가 구분하지 못한다는 점과 $D$에서 학습에 용이한 샘플을 구별하지 못한다는 점이 그것입니다.

4.1 Preprocessing and Model Architecture

아타리 프레임의 원본 데이터는 210x160의 128 색으로 컴퓨터 자원을 너무 많이 소모하기 때문에 별도의 전처리를 통해 입력 데이터의 차원을 줄였습니다. 우선 RGB는 grey scale로 전환하고, down sampling을 통해 110x84 크기로 이미지를 줄였습니다. 최종적인 이미지는 GPU가 정사각 입력값만 처리 할 수 있기 때문에 84x84로 임의로 이미지를 잘랐습니다. 이후 입력값을 representation으로 변환시키는 $\phi$로 이전의 4개의 프레임을 하나로 스택하도록 하였습니다.

기본적으로 Q는 과거의 행동을 Q-value를 추정하는 scalar로 맵핑합니다. 그리고 과거의 행동들은 Q의 입력값으로 사용되었습니다. 하지만 이러한 접근법은 각각의 행동에 대해 Q-value를 예측해야 하므로 선형적으로 연산량이 증가하게 됩니다. 그래서 저자들은 상태 표상(representation)만 입력값으로 하여 각 행동에 Q-value를 예측하도록 하였습니다. 이렇게 하여 각 출력값은 입력된 상태의 Q-value에 대응하게 됩니다. 이를 통해 하나의 순전파를 통해서도 주어진 상태에 대해 가능한 모든 행동의 Q-value를 구할 수 있게 됩니다.

전체 모델 구조는 다음과 같습니다.

• 입력값: $\phi$를 통해 생성된 84x84x4 이미지
• 첫번째 히든 레이어(Convolution layer): 8x8짜리 필터 16개(stride = 4, ReLU)
• 두번째 히든 레이어(Convolution layer): 4x4짜리 필터 32개(stride = 2, ReLU)
• 최종 히든 레이어(Fully Connected Unit): 256개 rectified unit
• 출력 레이어: 각 가능한 행동에 대한 하나의 노드
  -> 가능한 행동은 4개부터 18개까지 각 게임마다 저자들이 설정하였다.

5. Experiments

본 논문이 만든 모델의 장점한 모든 게임에 대해 동일한 파라미터와 구조를 공유하는 매우 강건한 모델이라는 점이다. 다만 저자들은 학습 과정에서 게임에 따라 보상을 변경했다고 한다. 그 이유는 게임마다 보상의 범위가 너무 차이가 나서 긍정적인 보상은 1, 부정적인 보상은 -1, 변화가 없을 경우 0으로 통일했다고 한다. 이를 통해 각 게임마다 다른 오차 범위 역시 제한되어 동일한 learning rate을 사용할 수 있었다. 하지만 당연하게도 성능에도 영향을 줄 수 밖에 없었다고 한다.

배치 사이즈는 32, optimizer는 RMSProp을 사용했다. 행동 정책은 100만번째 프레임까진 1부터 0.1까지 일정하게 감소하는 $\epsilon$을 사용하고 이후에는 0.1로 고정했다고 한다. 총 1000만 프레임을 학습에 사용했고, 최근 100만 프레임을 replay memory로 사용했다.

이전의 방법론과 같이 단순 frame skiiping을 사용했다. 이는 에이전트가 k번째 프레임마다 장면을 입력받고 선택하도록 하는 것으로 사이의 프레임에선 직전의 행동을 반복하도록 한다. 매 프레임마다 에이전트가 작동하도록 하는 것보다 frame skipping을 이용하여 더 적은 컴퓨터 자원을 소모시키므로, k배만큼 학습을 더 시킬 수 있다는 의미이기도 하다. 각 게임의 특성에 맞추어 k값은 조정되었다.

5.1 Training and Stability

지도학습에선 train 데이터와 evaluation 데이터를 매 학습마다 평가하여 성능을 비교적 실시간을 볼 수 있다. 하지만 강화학습에선 학습 과정 동안 그 성능을 정확하게 확인하는 것은 힘든 일이다. 본 논문은 평가 지표로 에이전트가 한 에피소드 당 획득한 총 리워드 혹은 전체 게임의 평균 리워드인데, 주기적으로 학습 동안 계산했다고 한다. 평균 전체 보상 지표는 노이즈가 매우 많은데 왜냐하면 정책에서 조그마한 변화가 상태 분포를 크게 변화시킬 수 있기 때문이다(지도학습으로 보자면 매 에포크마다 input data가 크게 바뀌면 성능이 엄청 요동치는 것과 동일하다.).

위 그래프의 왼쪽 두 개 플랏은 전체 보상의 평균이 에포크가 지나면서 어떻게 변화하는지 보여주고 있다(두 게임). 실제로 두 그래프는 무척 널뛰기를 하고 있는 모습을 보인다. 심지어 두번째 게임의 경우엔 어느 정도 학습이 이루어진 이후에도 아주 나쁜 리워드를 보이기도 했다.
이에 비해 안정적인 개선을 보이는 지표가 오른쪽에 있는 두 개의 플랏이다. 이는 Q함수의 action-value를 나타낸 것으로, 특정 state에서 에이전트가 얻을 수 있는 미래의 reward에 대한 할인율이 적용된 reward이다. 이는 에포크가 증가함에따라 실제로 얻은 리워드의 평균 그래프보다 훨씬 안정적으로 증가하는 모습을 보이고 있는데, 그래프에 나타나지 않은 다른 5개의 게임에서도 비슷한 양상을 보였다고 한다. 특히, 저자들은 실험 중 한번도 발산 이슈를 겪지 않았다고 하니, DQN의 안정적인 학습 성능을 알 수 있다.

5.2 Visualizing the Value Function

게임이 진행됨에 따라 가치 함수의 변화를 살펴보자. 실제 인간이 인식하는 게임 상황과 모델이 인식하는 reward가 비슷한지 살펴볼 필요가 있을 것이다.

위 표는 각각 A,B,C 시점에서의 학습된 value function을 나타낸 것이다. 해당 게임은 적선을 잡으면 점수가 오르는 게임인데, value function이 급증한 A는 실제로 새로운 적선이 등장한 시점이다. 또한, 에이전트는 A에서 어뢰를 발사하였고, 어뢰가 적선을 침몰시키기 직전인 B 시점에선 value function이 최고치를 달성한 것을 알 수 있다. 또한 적선이 사라지고 난 이후인 C 시점엔 평상시와 비슷한 value function을 보인다. 이는 모델이 복잡한 state와 연속적인 이벤트를 납득할만한 수준에서 파악하고 있다는 방증이기도 하다.

5.3 Main Evaluation

이번엔 아타리 게임에 대해 우수한 성능을 보인 다른 모델과 성능을 비교해보도록 하자. 논문에선 휴리스틱한 방법으로 feature extraction을 수행하고 선형 정책을 적용한 Sarsa 모델과 사전 학습된 방법으로 feature extraction을 수행하고 Sarsa 알고리즘을 사용하는 Contingency을 비교대상으로 삼았다. 두 모델 모두 사전 지식을 활용해 변수를 추출한다는 점에서 이미 DQN에 비해 단점을 가지고 있다고 할 수 있다.

두 모델 이외에도 게임을 잘하는 전문가의 스코어와 uniform distribution에서 랜덤하게 선택한 행동을 수행하는 정책을 비교대상으로 삼았다. 정책 은 $\epsilon$-greedy 정책을 $\epsilon = 0.05$으로, step 역시 고정하여 수행하였다. 그 결과는 다음과 같다.

결과는 인간과 동등한 성능을 보이거나 훨씬 뛰어넘는 성능을 보이기도 했다. 다른 모델 보다 훨씬 좋은 성능을 보이기도 했다. 특히 HNeat Pixel은 아타리 에뮬레이터로부터 8개의 사물에 대한 맵핑된 representation을 가져옴에도 불구하고 DQN이 성능이 좋았다. 사람에 비해 성능이 떨어지는 3개의 게임은 장기적으로 결과를 추정해야 하므로 사람에 비해 성능이 떨어지는 것으로 분석된다.

6. Conclusion

이 모델이 돌파한 challenge들은 다음과 같다.

• 같은 모델 구조와 파라미터를 가지고 다양한 게임에서 준수한 성능을 이끌어냈다.
• raw pixel data를 이용한 end to end 모델이다.
• SGD, replay memory 등의 개념을 Q-learning과 결합했다.

참고

https://mangkyu.tistory.com/60
https://hugrypiggykim.com/2019/03/10/playing-atari-with-deep-reinforcement-learning/