Summary

Different types of tasks :

• Node level
• Edge level
• Graph level

Choice of a graph representation

• Directed
• Undirected
• Bipartite
• Weighted Edge
• Advacency Matrix
• Connectivity

투빅스 사람들과 함께 GNN 스터디를 시작했다. 유튜브에 공개된 스탠포드 대학의 CS224W 강의를 기반으로 진행될 예정이다.

그래프 이론들이 자연어에서 지식 그래프 등으로 활발히 활용되고, 이외에도 다양한 방식으로 활용되는 것 같아 이후에 어떻게 사용될지 모르지만 우선 학습해두고자 한다. (사실 그냥 궁금하다.)

0. Why Graphs?

왜 그래프를 배워야 하는지 우선 생각해보고 시작하자.

그래프란 두 요소의 관계 혹은 상호 작용을 표현하고 분석할 수 있는 일반적인 언어다.
Graphs are a general language for describing and analyzing entities with relations/interactios

라고 강의에서는 소개하고 있다.

현실 세계의 현상들은 단순히 각 요소들이 독립적으로 존재하거나, 발생하지 않습니다. 다양한 요소들이 서로 영향을 주고 받으며 존재하고 발생하게 됩니다. 그래프는 이런 상황을 효과적으로 표현할 수 있게 해줍니다.

대표적으로 지하철 노선, 소셜 네트워크, 뉴런의 상호작용, 인터넷 사용자의 활동 기록 등이 요소 간의 상호작용으로 이루어집니다. 또한 지식 그래프처럼 사실들이 어떻게 연관되어 있는지를 표현할 수도 있습니다.

1. Types of Networks and Graphs

네트워크 혹은 그래프는 두가지 종류가 있습니다.

1-1. Networks (also known as Natural Graphs)

기본적으로 원래 네트워크나 그래프의 형태로 이루어진 데이터입니다. 즉, 우리가 임의로 그래프의 형태로 만들어주는 것이 아니라, 원래 그래프의 형태를 가지고 있습니다.

1. Social networks
   사회라는 그래프는 700만 개의 요소들이 관계를 맺고 있는 그래프라고 간주할 수 있습니다.
2. Communication and transactions
   전자기기 간의 소통이나 채권 거래 등의 형태는 요소 간의 상호 작용으로 표현됩니다.
3. Biomedicine
   생물은 결국 세포나 유전자의 관계를 통해 삶을 영위하게 됩니다.
4. Brain Connections
   인간의 두뇌에서 이루어지는 사고작용은 수많은 뉴런들의 상호작용으로 구성되어 있습니다.

1-2. Graphs(as a representation)

실제로 그래프의 모습을 가지고 있지 않지만, 임의의 방법을 통해 그래프로 나타낼 수 있는 데이터들도 있습니다.

1. Information/Knowledge
   지식과 정보를 정리하고 그 관계를 연결하여 그래프로 나타낼 수 있다.
2. Software
3. Similarity networks
4. Relational Structures
   화학 분야에서 분자와 원자의 구조, 물리학에서 입자의 움직임 등을 그래프로 나타낼 수 있다.

2. Graph in ML, DL

그렇다면 나를 비롯해서 ML과 DL 등의 다양한 분야의 사람들이 그래프를 배워야하는 이유는 무엇일까? 무엇이 그래프를 배워야 하는 분야로 만드는 것인가?

간단히 말하면 "성능이 좋아지니까!"이다.

좀 더 자세히 말해보자면, 시간이 지날수록 두 분야에서는 복잡한 관계를 모델링하고자 한다. 과거엔 붓꽃의 꽃받침 크기, 너비 등으로 붓꽃의 종류를 맞추는 수준이었다면, 이제는 질의 관계를 모델링하고, 더 나아가 그 과정에서 사용되는 논리 구조나 근거 역시 모델링하려 하고 있다. 이러한 복잡한 관계는 당연히 데이터에 잠재되어 있고, 모델은 이를 패턴화하여 인식하는 것이다.

기존의 모델은 내재된 패턴을 인식하려한다. 하지만 그래프는 그 복잡한 관계를 끌어낼 수 있다. 명시적으로 복잡한 관계를 잡아내서, 모델의 입력에 활용할 수 있다면, 당연히 그 성능은 비약적으로 상승하게 될 것이다.

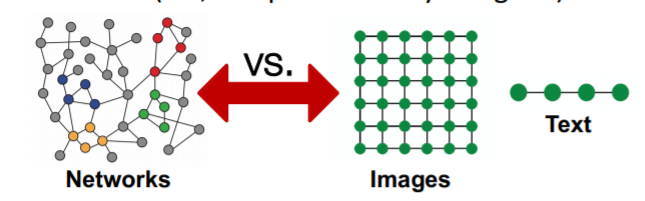
단순하게 생각하면 CNN은 그리드 형식의 데이터 관계를 다루고, RNN은 시간에 대해 선형적인 데이터 관계를 다루게 된다. 하지만 이미지가 정말 그리드 형태이고, 음성과 텍스트가 시간에 선형적인가? 그렇지 않아서 수많은 복잡한 모델이 개발되고 있는 것이 아닌가? 복잡한 관계를 그래프로 나타낼 수 있다면 더 효과적인 모델링이 가능할 것이다.

3. So... What are we going to do in this lecture?

기존의 DL, ML이 그래프에 비해 쉽지 않다는 것은 알겠다. 그렇다면 이 수업에선 뭘 하려고 하는 걸까?

1. Neural Network
   어쨌든 신경망을 이용한 수업이 될 것이다.

2. Graph Input
   하지만 입력값은 벡터나 텐서가 아니라 그래프 구조가 될 것이다.

3. Predict Graph
   물론 예측도 하게 된다. 하지만 단순한 레이블 보다는 노드의 레이블, 새로운 연결, 혹은 아예 새로운 그래프를 예측하게 된다.

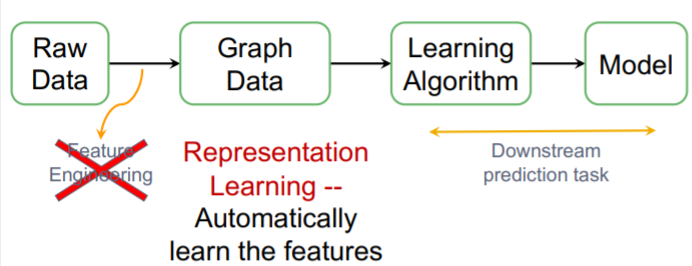
3-1. Representation Learning

representation learning이란 특정 변수를 함수 f(x)를 통해 벡터화 시키는 것을 의미한다. NLP에서 사용하는 임베딩 벡터가 바로 그 사례이다. 그래프에선 특정 노드를 입력받은 함수 f가 이를 임베딩하여 벡터화시키게 된다. 이때, 노드의 값, 주변 링크의 값, 주변 그래프 구조 등 다양한 값을 입력으로 사용할 수 있다. 그리고 함수 f(x)는 당연하게도 신경망 기반 모델이 되게 된다.
위 도식은 전통적인 ML 프로세스를 나타낸다. 데이터에서 정교한 엔지니어링을 통해 최적의 변수를 찾고 이를 기반으로 모델링하여 예측값을 산출하게 된다. 하지만 도메인마다, 사례마다 새로 데이터 엔지니어링이 필요하다.

그래서 그래프를 이용해 데이터 엔지니어링을 대체해보고자 한다. representation learning을 이용해 변수를 따로 엔지니어링하지 않고 효과적으로 사용해보자.

이 수업에선 그래서 전통적인 그래프 모델에서부터 기본적인 GNN, 다양한 딥러닝 기반 그래프 모델들과 그 적용 분야에 대해 공부하게 될 것이다.

4. Types of Tasks

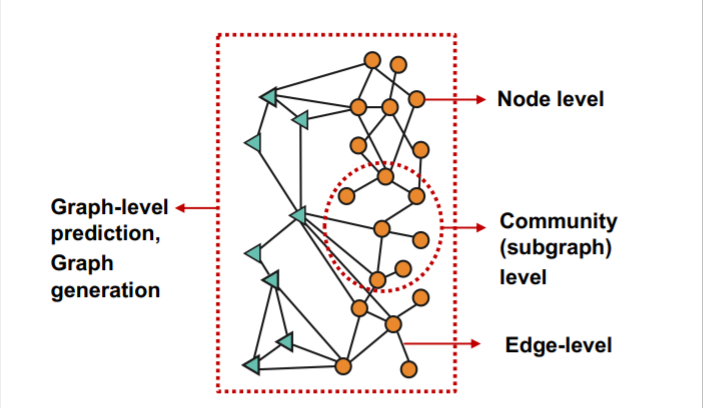
그래프 분야의 태스크는 크게 단일 노드 단위, 단일 엣지 단위, 부분그래프 단위, 전체 그래프 단위 태스크로 나뉘게 된다.

1. Node Classification
   노드 분류는 온라인 유저나 아이템 분류시 사용되는 태스크로 단일 노드 단위의 태스크이다.

2. Link Prediction
   링크 예측은 지식 그래프에서 사용되는 태스크로 엣지 단위 태스크이다. 두 노드 간의 관계를 모델링하게 된다.

3. Graph Classification
   그래프 분류는 화학구조 특징 예측 등에 사용되어 신약 개발에 활용되는 태스크로 그래프 전체를 이용해 해당 그래프를 분류하는 태스크이다.

4. Clustering
   클러스터링은 일부 노드들이 커뮤니티(부분 그래프)를 형성하는지 감지하는 태스크로, 소셜 군집 감지 등에 사용된다.

5. Etc...
   이외에도 Graph generation은 신약 개발에 사용되는 태스크이고, Graph evolution은 물리학에서 시뮬레이션 시 사용되는 태스크이다.

4-1 Applications

1. Node Level
   2020월 12월 중순 구글 딥마인드는 단백질 구조를 예측하는 태스크에서 혁신적인 개선을 보인 모델을 선보였다. 단백질은 아미노산이 체인처럼 연결되어 있는 구조인데, 문제는 자성과 화학적 구조 등에 의해 이 체인이 꼬이고 접히게 된다는 점이다.
   
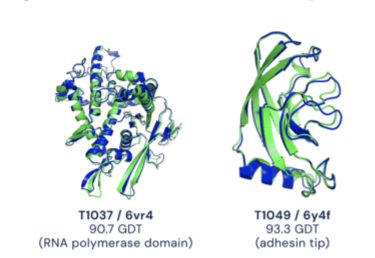
   그래서 위 그림처럼 단백질은 하나의 선이 복잡하게 얽힌 구조를 가지게 된다. 딥마인드는 아미노산 하나를 노드로 설정하고, 아미노산 간의 거리를 엣지로 하여 GNN을 적용하였다고 한다. 그 결과 이전에 비해 효과적으로 모델링할 수 있었고, 그 정확도가 획기적으로 개선되었다고 한다.

2. Edge Level
   중증 환자 혹은 고령 환자의 경우 한번에 여러 약을 복용하게 된다. 다양하고 심각한 질환에 대응해야 하기 때문이다. 하지만 이렇게 여러 약, 많게는 20알이 넘게 한번에 복용하다보면 예기치 못한 부작용을 겪게 된다. 하지만 약의 종류는 너무 많아서, 모든 조합의 부작용을 실험할 수 없다. 이에 그래프 문제로 전환하여 해결할 수 있다.
   
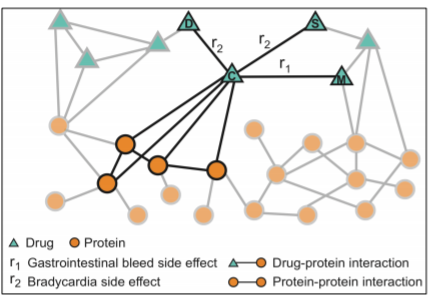
   위의 그림에서 세모 노드는 약이고, 동그란 노드는 인간의 단백질이다. 약과 단백질 간의 엣지는 해당 약이 타겟으로 작용하고자 하는 단백질과의 연결이다. 단백질 간의 연결은 기존의 생리학적 연구들을 통해 밝혀진 단백질 간의 상관관계와 작용 방식을 이용해 구성하게 된다. 또한, 약들 간의 엣지는 해당 조합의 약을 복용할 경우 발생하는 부작용이 된다. 하지만 모든 약 조합의 부작용을 알지 못하기 때문에, 당연하게도 엣지들이 무척이나 비어 있게 되고, 이 엣지들을 채우는 태스크로 전환된다.

3. Subgraph Level
   구글맵, 네이버 지도 등을 통해 경로를 탐색하고 예측되는 시간을 추정할 때, 그래프가 사용된다고 한다. 각 도로가 노드가 되고, 도로에서 도로로 건너가는 시간이 엣지가 되어, 이를 학습하게 되면, 출발지에서 목적지까지 소요되는 시간을 추정하는 GNN 모델을 개발할 수 있다고 한다.

4. Graph Level
   그래프 생성 및 진화 태스크에서는 분자 구조 이야기가 많이 나왔다.
   
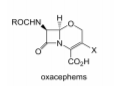
   분자는 기본적으로 원자와 원자 간의 화학적 결합으로 이루어져 있는데, 이는 그래프 형태라고 할 수 있다. 원자는 노드로, 화학적 결합은 엣지로 표현 가능하기 때문이다. 이를 통해 원하는 효과를 가지는 신약 개발이나 현재 약의 효과를 보강할 수 있는 분자 구조 생성 등이 가능해진다.

5. Choice of Graph Representation

위와 같은 그래프가 있다고 해보자. 그래프는 두가지 요소로 이루어져 있다.

• Node : 노드는 그래프를 이루는 각 개체로 node 혹은 vertice로 표현한다고 한다. 또한 N으로 나타낸다.
• Interactions : 노드 간의 상호작용은 link 혹은 edge로 표현되며 E로 나타낸다.
• System : 노드들과 엣지들로 이루어진 전체 그래프는 network 혹은 graph로 표현되며 그래프를 이루는 노드와 엣지 집합을 이용해 G(N, E)로 나타낸다.

우리가 어떠한 데이터를 그래프로 나타낼 때 무엇을 노드와 엣지로 할 지 선택하는 것은 매우 중요하다고 할 수 있다.

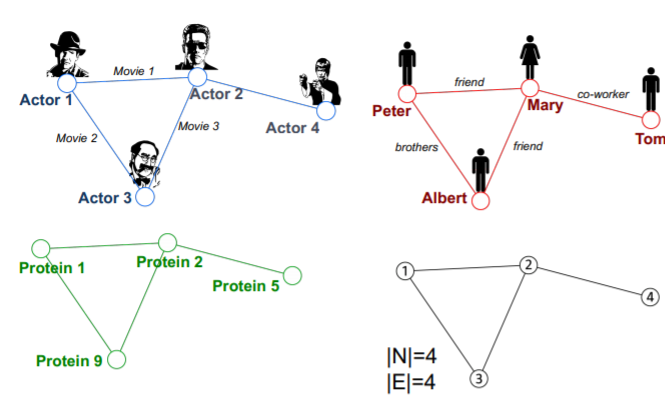
위 그림처럼 각기 다른 데이터라 하더라도 동일한 그래프 구조로 표현될 수 있고, 반대로 동일한 데이터라도 다른 그래프 구조를 만들 수 있기 때문이다.

사회를 그래프로 표현할 때 직업적 관계를 엣지로 가지면 직업과 관련된 그래프가 표현되겠지만, 성관계를 엣지로 가지면 성생활 네트워크가 그래프로 표현되게 될 것이다.

6. Types of Graphs

Node degree : 노드에 연결된 엣지의 수를 의미하게 된다.

6-1. Undirected vs Directed

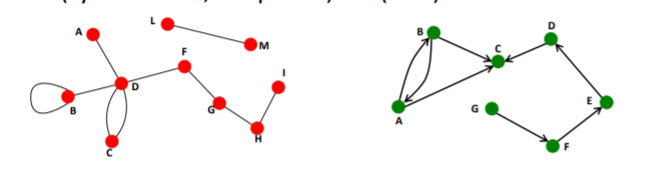
Undirected 그래프는 엣지에 방향성이 없는 그래프이다. 즉, 엣지가 대칭적인 형태를 가진다. 주로 협업이나 친구 등의 상호적 관계를 나타낼 때 사용된다.
Node degree, $k_i$는 i 노드에 연결되어 있는 모든 엣지의 수이다.
평균 Node degree는 $\bar{k} = < k > = {1 \over N}\sum^N_{i = 1}k_j = {2E \over N}$

Undirected 그래프는 degree를 셀 때 각 엣지가 각 노드마다 중복되어 세지기 때문에 Avg. Node Degree 식의 분자는 2E가 되게 된다.

Directed 그래프는 엣지에 방향성이 있는 그래프로 출발 노드와 도착 노드가 구분된다. 주로 트위터 등의 팔로우 관계, 전화 수발신 기록 등이 이를 통해 표현된다.

Node degree는 엣지의 출발과 도착에 따라 두가지가 있다.
k^{in}은 해당 노드가 도착지인 엣지에 대한 degree이고, k^{out}은 해당 노드가 출발지인 엣지에 대한 degree가 된다.

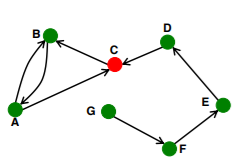
위의 그래프에선 다음과 같다.

$k^{in}_C = 2, k^{out}_C = 1, K_C = 3$

$\bar{k} = {E \over N}, \bar{k^{in}} = \bar{k^{out}}$

6-2. Bipartite Graph

Bipartite Graph는 두 노드 집합으로 나눠질 수 있는 그래프를 의미한다. 이때 두 노드 집합은 내부에는 엣지가 없고, 두 집합 간에만 엣지가 존재한다. 즉, 두 노드 집합을 U와 V라고 할 때, U와 V는 서로 독립적인 집합이 된다.

그 예시로는 다음과 같은 데이터들이 있다.

• 저자 - 논문
• 배우 - 영화
• 사용자 - 영화 (리뷰)
• 레시피 - 재료

또한 이러한 Bipartite Grph는 두 노드 집합의 결합이라는 점에서 이를 분리해서 다시 하나의 노드 집합으로 나타낼 수도 있는데, 이를 Folded network라고 부른다. 또한 이 과정을 Projection이라고 하는데 선형대수학의 사영과 비슷한 개념인지는 확실하지 않아 project로 표현하겠다.

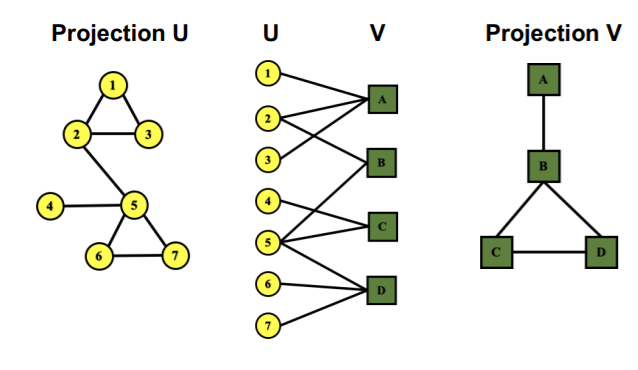
위 그림에서 가운데에 있는 Bipartite Graph를 접어서 U와 V projection으로 나타내면 각각 좌우에 위치한 그래프가 된다. 1과 2가 A에 연결되어 있으므로, 1과 2는 서로 연결될 수 있고, A와 B는 2와 연결되어 있으므로 A와 B는 연결될 수 있어, 이렇게 접은 그래프가 만들어지게 된다.

6-3. Adjacency Matrix

그럼 그래프를 실제로 어떻게 표현할 수 있을까? 가장 단순한 방법으론 행렬로 표현 할 수 있을 것이다.

$A_{ij} = 1$ if there is a link from node i to node j
$A_{ij} = 0$ if there is not a link from node i to node j

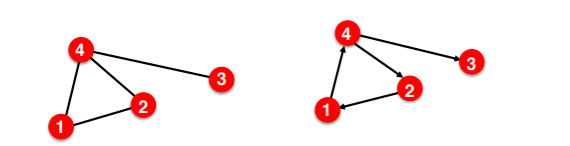
그런데 이는 Directed Graph인지 Undirected Graph인지에 따라 다른 형태를 지니게 된다. 위의 두 그래프를 Advacency Matrix로 나타내면 아래와 같다.

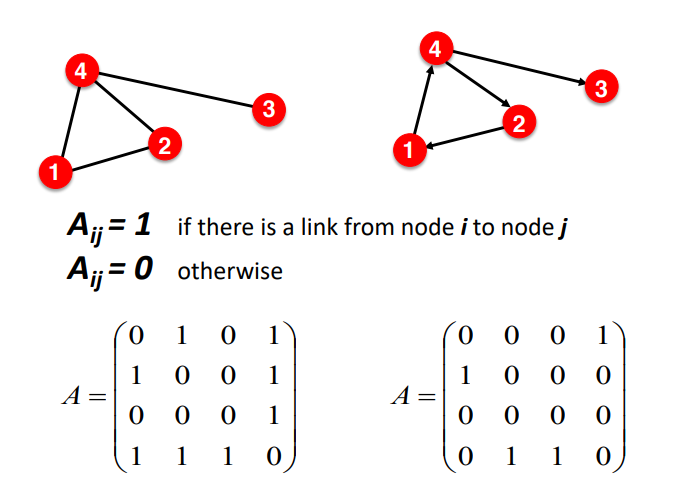
Undirected Graph는 하나의 엣지에 연결된 두 노드 모두의 element가 1이 되므로 대칭행렬이 된다. 하지만 Directed Graph는 방향서을 가지고 있기 때문에 대칭행렬이 될 수 없다.

이와 더불어서 Undirected Graph는 대칭행렬이므로 하나의 노드의 degree는 해당 노드의 행 또는 열의 원소의 합과 같다. Directed Graph는 대칭행렬이 아니므로 행과 열이 각각 해당 노드를 도착지로 갖는 엣지에 대한 degree이거나 출발지로 갖는 엣지에 대한 degree가 된다.

6-4. Adjacency Matrix are Sparse

실제 세계의 인접행렬은 매우매우 sparse해진다.

위 그림은 강의에서 보여준 인접행렬인데, 비어있는 값이 훨씬 많은 것을 볼 수 있다.
어찌 생각해보면 당연한 결과이다. 하나의 노드가 만날 수 있는 다른 노드는 한정적일 수 밖에 없다. 소셜 네트워크를 보면, 한 명의 사람이 팔로우하거나 친구를 맺을 수 있는 인원은 많아 봤자 500명 내외일 것이다. 분자 구조를 생각해도, 하나의 원자가 100개 이상의 원자와 연결될 수는 없다. 그래서 교수님은 우리가 다룰 Graph들은 대부분 sparse matrix가 될 것이라 이야기하신다.

6-5. Edge List

그래프를 표현하는 또다른 방법은 엣지 리스트가 있다. 엣지로 연결된 두 노드만 이용하여 표현하는 건데, 다음과 같다.

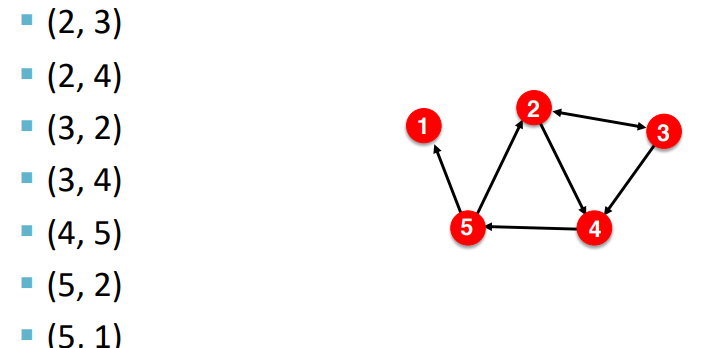
직관적이고, 딥러닝 분야에서 많이 사용되는 표현방식이라고 한다. 하지만, 이렇게 표현하면 degree 계산이나 그래프 분석이 어려워진다고 한다. 두 노드의 관계는 보이지만, 전체 구조를 보기 힘들어진다는 이야기인 것 같다.

6-6. Advacency List

인접행렬은 너무 sparse해서 메모리 등의 낭비가 있을 것이고(물론 언어마다 sparse matrix를 따로 다뤄서 메모리 소모를 줄이기는 한다.) 엣지 리스트는 분석이 어려워진다는 단점이 있었다. 두 방법을 보완한 것이 인접 리스트이다. 인접 리스트는 네트워크가 커지고, sparse할 때 효과적으로 다룰 수 있다는 장점이 있다.

인접 리스트로 그래프를 표현해보면 다음과 같다.

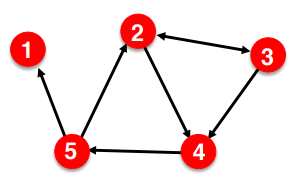
• 1 :
• 2 : 3, 4
• 3 : 2, 4
• 4 : 5
• 5 : 1, 2

즉 각 노드가 인접한 노드를 리스트로 표현한 것이다. Undirected Graph의 경우엔 위의 방법을 사용하면 되고, Directed Graph의 경우에는 Incoming 혹은 Outgoing Edge만 표현하면 될 것이다.

7. Various Graph Property

그래프는 단순히 노드와 각 노드 간 하나의 엣지로만 이루어져 있지 않다.

각 노드 연결의 강도를 나타내는 weight나, 하나의 노드가 다른 노드와 연결된 순위를 정하는 ranking이나, 연결의 종류를 의미하는 type 등으로 엣지가 다양하게 표현될 수도 있다.

또한, 각 노드가 가지는 요소들이 여러가지일 수도 있다. 소셜 네트워크에선 나이, 성별, 거주지, 직업 등이 노드가 가질 수 있는 요소가 될 것이다.

이를 표현하는 방법은 인접행렬에서 단순히 바이너리로 표현하던 것을 float으로 표현하면 된다.

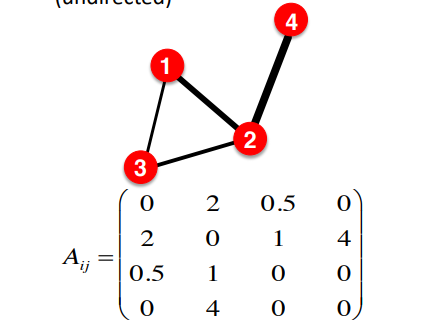
즉, weight를 엣지에 추가한다면 위와 같이 표현할 수 있게 된다. 이때의 degree는 단순한 count가 아니라 0이 아닌 값들을 카운트하게 된다.

이외에도 다음과 같은 요소들이 있다.

-self edge(self loop)
: 노드가 스스로 연결되어 엣지를 가질 수도 있다. 이때는 인접 행렬에서 대각 성분에 값을 가지고 있게 된다.

• Multigraph
  : 두 노드의 연결이 하나의 엣지가 아니라 여러 엣지로 표현될 수도 있다. 위에서 언급한 다양한 엣지의 요소들을 표현하고자 한다면 두 노드 사이에도 여러 개의 엣지가 필요할 것이다.

• Connectivity of Undirected Graph
  :
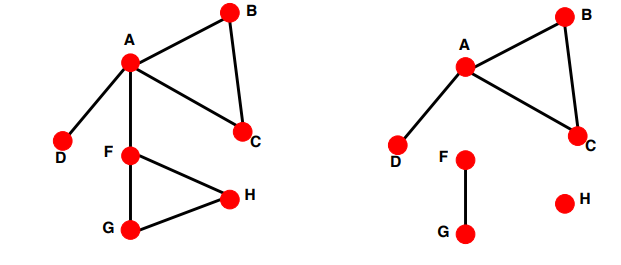
  위 그림에서 왼쪽 그래프는 모든 노드가 엣지로 연결되어 있는 모습을 보이지만, 오른쪽 그래프는 일부 노드가 연결되어 있지 않다. 특히 H 노드의 경우 어떠한 노드와도 연결되어 있지 않은 고립된(isolated) 노드이다.
  이러한 Connectivity는 인접행렬로 표현하게 되면 재밌는 모습을 보이게 된다.
  
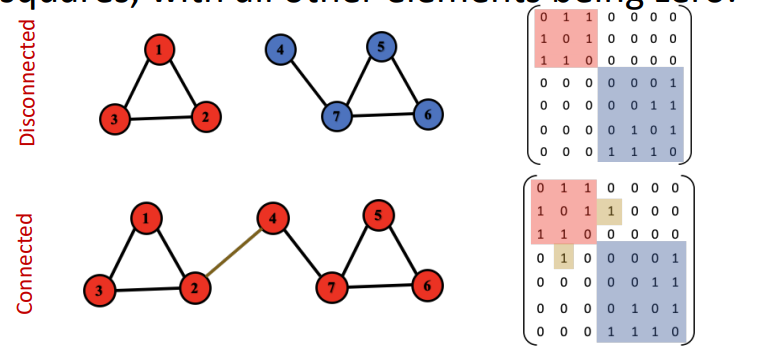
  연결되지 않은 그래프의 인접행렬은 대각 성분에 부분 행렬을 가지게 된다(이 표현이 맞는지 모르겠다). 하지만 하나의 노드라도 연결된 그래프라면 아래의 그림과 같이 대각 성분에 부분행렬 외에도 다른 element에 0이 아닌 값을 가지게 된다.

• Connectivity of Directed Graph
  Directed Graph에서의 연결성은 조금 다르다. 강한 연결과 약한 연결로 구분한다. Directed 라는 것은 엣지에 방향성이 있다는 말이 되므로, 이 방향성과 연결의 강도가 관련이 있다.

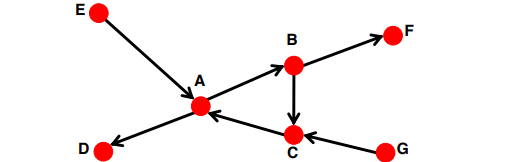
위 그래프에서 A, B, C 노드는 서로 강한 연결을 가지고 있다. 세 노드끼리는 엣지를 통해 직접 연결되어 있기 때문이다. 하지만 E와 A 노드 간에는 약한 연결이 있다. E에서 A로만 엣지가 연결되어 있어, A 에서 E 방향으로 향할 수 있는 엣지가 없기 때문이다.

• Strongly Connected components(SCCs)
  
  : 이를 좀더 복잡한 그래프에서 살펴보면 위 그림과 같다. 즉, Directed Graph의 전체 부분이 강하게 연결되어 있지 않지만, 부분 그래프가 강하게 연결되어 있는 SCC가 있을 수 있는 것이다.

---

참고

CS224W 1강
CS224W 강의 자료