0. Intro
이전의 강의에서 그래프를 이용한 머신러닝은 세가지 차원에서 다뤄진다고 했다.
Node, Line, Graph 세가지 차원이다.
- Node level prediction은 해당 노드의 특징들이 어떠한 지 예측한다.
- Link level prediction은 두 노드 간의 링크의 강도 혹은 연결 여부를 예측한다.
- Graph level prediction은 새로운 노드가 주어졌을 때, 전체 구조에서 어떻게 형성되는지를 예측하게 된다.
이번 시간에는 그래프를 입력값으로 하는 머신러닝에서 새로운 변수가 주어졌을 때, 이것으로 인해 전체 구조가 어떻게 변할지 살펴볼 것이다.
그래프를 이용한다고 해서 전반적인 머신러닝 파이프라인이 변하지 않는다.
주어진 값들은 벡터 형태의 변수가 되고, 이를 이용해 Node, Link, Graph level의 레이블을 짝지어 학습한다. 그리고 다시 벡터 형태의 변수를 가지는 node, link, graph가 주어졌을 때, 이를 예측하게 된다.
전통적인 머신러닝 기법은 feature engineering이 직접 가해지게 되는데, 이번 시간에는 GNN을 제외한 전통적인 머신러닝 기법을 다루게 된다. 또한, 간단한 개념을 이용하기 위해 Undirected Graph로 한정짓는다.
1. Goal
전반적인 파이프라인은 같지만, 우리에게 주어지는 것이 (case, feature) 형태의 매트릭스가 아니라 노드와 엣지로 이루어진 그래프 형태라는 점이 다르다. 즉
이 상황에서
이런 함수 f를 찾고자 하는 것이다. 여기서 레이블은 노드의 변수값, 링크의 강도, 노드의 연결 여부 등 다양한 실수가 될 수 있다.
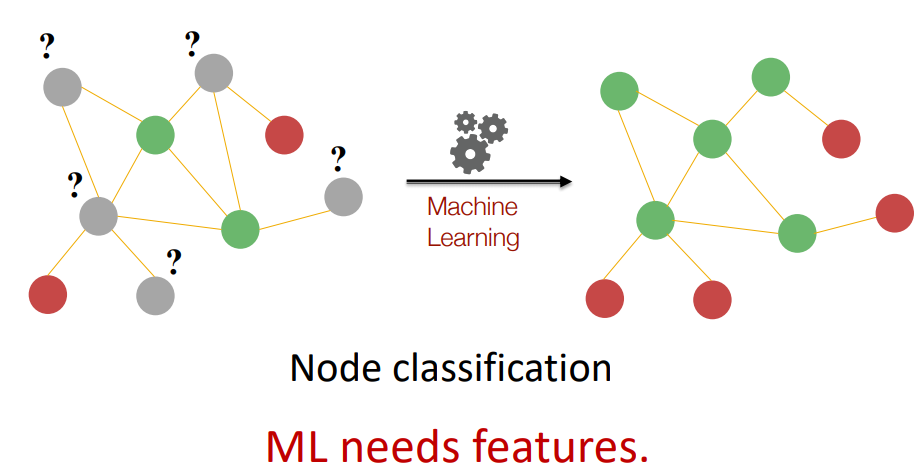
기존의 머신러닝과 다른 부분이 여기 있다고 생각하는데, 위 그림에서 입력값은 왼쪽 그림이다. node level prediction의 경우 위와 같이 전체 그래프 구조는 주어진 상태에서 각각의 노드의 레이블을 예측하게 되는 것이다. 위 그림은 하나의 엣지만 가지면 빨간색, 두개 이상의 엣지를 가지면 녹색임을 알 수 있다.
그렇다면 어떻게 그래프의 구조를 변수화하여 머신러닝의 입력으로 사용할 수 있을까?
이 수업에선 총 네가지 방법을 배우게 된다.
- Node Degree : 이전 시간에 배웠던 개념이다.
- Node Centrality : 노드가 전체 그래프에서 얼마나 중심에 위치하는지이다.
- Clustering Coefficient : 전체 그래프의 구조에서 해당 노드의 의미를 살피는 것이라고 한다.
- Graphlets
2. Node Degree
node degree는 단순하다. 해당 노드가 몇개의 엣지를 가지고 있는지를 의미한다. 단순한만큼 사용하기도 편하지만 문제점도 크다.
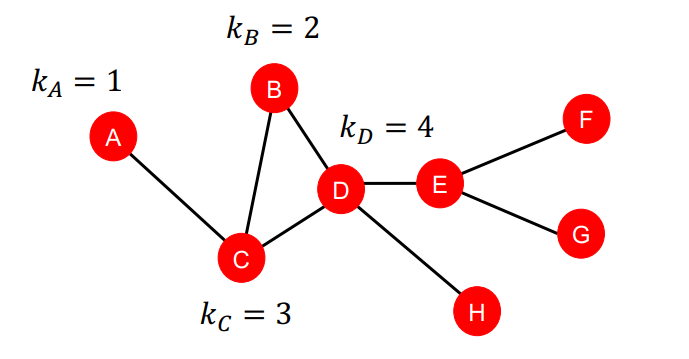
연결된 엣지의 갯수는 사실 그렇게 다양할 수 없다. 이전에도 말했듯이, 하나의 노드는 그렇게 많은 노드와 연결될 수 없는 것이 현실 세계의 데이터이다. 그러므로 degree가 비슷한 노드는 수없이 많을 수 밖에 없다. 하지만 정말 해당 노드들이 비슷한 특성을 가지는지는 고민이 필요하다. 위의 그래프에서도 A, H, G, F 노드 모두 degree가 1이지만, 각각이 그래프에서 차지하는 위치가 다르다. 즉, Node Degree만으론 각 노드의 특징을 충분히 볼 수 없다.
3. Node Centrality
Node Degree가 단순히 엣지의 수를 세서 제대로 노드의 특징을 담을 수 없다면, 각 노드가 그래프에서 어떤 의미를 지니는지 담고자 한 것이 Node Centrality이다. 이는 각각의 노드가 그래프에서 어디에 위치하는지에 대한 정보를 담게 된다. 대표적인 방법으론 다음과 같은 것들이 있다고 한다.
- Eigenvector centrality
- Betweenness centrality
- Closeness centrality
3-1. Eigenvector Centrality
아이겐 벡터 중심성은 어떤 노드 v의 주변에 있는 노드들이 중요한 노드들이라면 v 역시 중요한 노드라고 간주한다. 이를 식으로 나타내면 다음과 같다.
여기서 는 임의의 양의 상수이다. 하지만 이렇게 풀자면, 결국 v 노드 중심의 중요한 노드를 알아야 하는 재귀적 문제에 빠지게 된다. 이를 해결하기 위해 위 식을 약간 바꿔보자.
여기서 summation 함수를 행렬과 벡터로 표현할 수 있다(NLP의 Embedding 레이어처럼).
이랫더니, 선형대수학에서 정말 많이 봤던 식이 나왔다. 즉, 는 아이겐벨루, 는 아이겐벡터가 된다.
여기서 A는 인접행렬이 될 것이고, 는 중심성 벡터가 된다. 아이겐값 중 가장 큰 값 는 Perron-Frobenius 정리에 의해 항상 양의 값이고 유니크하다고 한다. 여기서 Perron-Frobenius 정리는 '0보다 큰 값을 가지는 행렬 A는 항상 양수인 dominant eigenvalue를 가진다'는 정리이다.
즉, 아이겐 벡터 개념을 이용하면, 인접 행렬에서 중심이 되는 노드를 산출할 수 있다는 것이 중요한 내용인 것 같다. 자세한 내용은 4강에서 Pagerank를 배우며 소개하는 것 같으니 이정도 하고 넘어가자.
3-2. Betweenness Centrality
betweenness centrality는 주변 노드와의 관계를 직접 살펴보는 방법이다. 우선 식은 다음과 같다.

위 그래프에서 는 당연히 0이다. A를 거쳐서는 어떤 두 노드도 최단 경로를 가질 수 없기 때문이다. 이에 반해 는 3이다. (A, E), (C, E), (B, E)로 가는 최단 경로는 D를 거쳐야 하기 때문이다. 이와 같이 betweenness centrality는 다른 노드로 가는 최단 경로에 놓여있는 노드를 중심이 되는 노드로 여긴다.
3-3. Closeness Centrality
Closeness centrality는 다른 노드로 가는 최단 경로가 짧을수록 중심 노드라고 본다.
즉, 위의 예시에서 가 된다.
하지만 로 더 작은 값을 가지게 된다. C 노드가 그래프의 중심에 가까워서 다른 노드와 최단거리가 짧아졌다고 보는 것이다.
3-4. Clustering Coefficient
Clustering coefficient는 그래프 전체를 고려하지 않고, 해당 노드의 주변 부분 그래프만 살펴보게 된다. 해당 노드의 이웃 노드가 서로 얼마나 연결되어 있는지 보는 것이다. 즉, 중심 노드라면 중심 노드 주변의 이웃노드들이 당연히 서로 연결되어 있어야 한다고 생각한다.
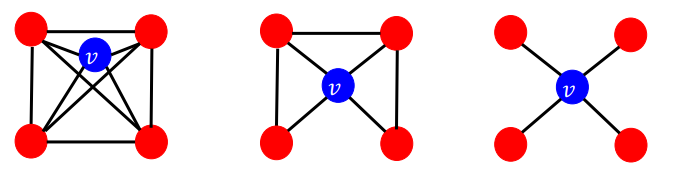
위 그림에서 v 노드는 모두 이웃 노드 4개를 가지고 있지만 이웃 노드 간의 엣지 수가 다르다. 왼쪽 그림의 경우 이웃 노드가 모두 연결되어 있으므로 이 된다. 하지만 가운데 그림의 경우 이웃 노드들이 최대 6개의 엣지를 가질 수 있는데 그 절반인 3개만 연결되어 있어 가 되게 되는 것이다.
3-5. Graphlets
위에서 예시로 들었던 그래프를 다시한번 살펴보자.
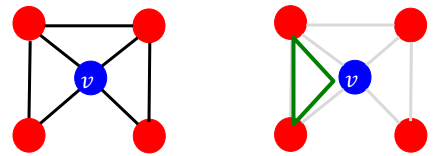
소셜 네트워크를 예시로 들어보면, 내 친구 a와 다른 친구 b는 시간이 흐르면서 친구가 될 수 있다. 만약 내가 좀더 외향적이고, 사교관계에서 중심을 이룬다면, 더 빨리 친구가 될 것이다. 즉, 노드 v의 이웃 노드들끼리 이어져 있을수록, 노드 v는 중심노드라고 할 수 있다. 위의 그림에선, 오른쪽처럼 삼각형을 이루면, 노드 v가 중심이 될 조건이 채워지게 되는 것이다.
여기서 삼각형과 같이, 노드 v가 중심노드로서 역할을 하게 하는 구조를 graphlet이라고 한다. 그렇다면 우리가 찾고자 하는 것은, 노드 v와 주변 노드들이 graphlet을 이룰 수 있는 경우의 수 중에 얼마나 이루고 있는지 보면 된다.
다섯개의 노드가 이룰 수 있는 graphlet은 총 73가지나 된다.
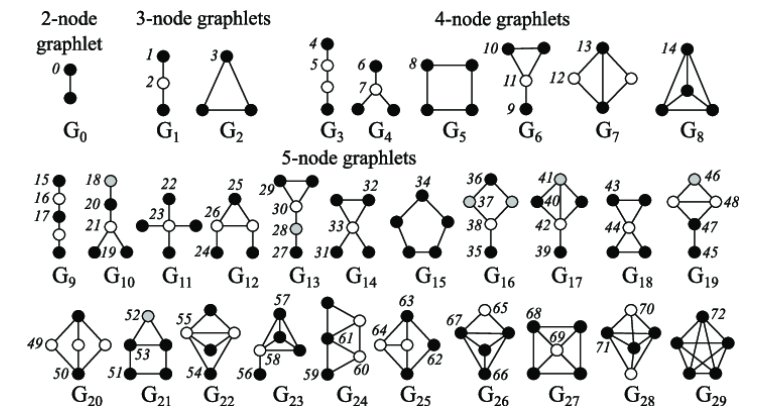
하지만 여기서 하나의 graphlet에서도 어느 점에 기준 노드를 둘 지에 따라 여러가지가 될 수 있다. G7을 보면 검은점과 흰 점은 서로 다르다. 하지만 검은 점 두개는 사실 서로 똑같은 위치를 가지고 있다. 반전 시키거나 회전시켜도 변하지 않기 때문이다. 이를 수학적으로 동형 사상이라고 한다는데, 이걸 다루기 시작하려면 공부해야하는게 넘쳐나고, GNN 수업을 들을 수 없을 것 같아, 나중에 필요해지면 다시 이야기해보도록 하자.
중요한 것은, graphlet 이 될 수 있는 모양은 많고, 하나의 모양에서도 위치에 따라 달라진다는 점이다.
- Degree : degree는 단순히 노드와 연결된 엣지의 갯수를 센다.
- Clustering Coefficient : clustering coefficient는 해당 노드를 기준으로 형성되는 삼각형의 갯수를 센다.
- Graphlet Degree Vector(GDV) : GDV는 다양한 graphlet에 대한 degree를 벡터로 표현한 것이다. GDV는 결국 해당 노드를 기준으로 각각의 graphlet이 몇개나 형성되었는지 센다.
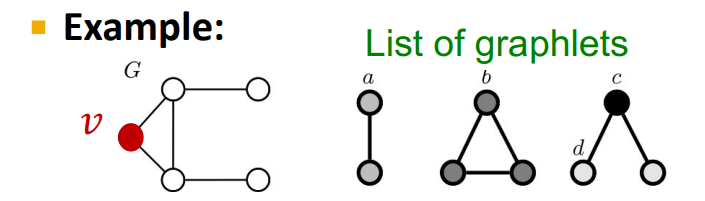
예를 들어 위와 같은 그래프오 graphlet 리스트가 있다고 가정해보자. 그러면 아래와 같이 graphlet의 갯수를 셀 수 있다.

이를 벡터로 표현하면 다음과 같이 표현할 수 있게 된다.
a, b, c, d
[2, 1, 0, 2]
만약 중심이 되는 노드 v를 포함해 5개의 노드로 graphlet을 계산하고자 한다면 총 73개의 graphlet을 계산하게 되고, 73차원 벡터로 표현가능하기 때문에, 변수가 73개 생성되게 된다. 또한, 해당 변수는 각각의 노드에 대해 거리가 4인 부분 그래프의 구조를 고려하게 되는 것이다.
즉, Graphlet Degerr Vector는 특정 노드의 부분 그래프의 위상적 특징을 추출할 수 있게 된다.
이를 통해 GDV는 단순한 node degree나 clustering coefficient에 비해 좀 더 위상학적으로 유사한 노드를 볼 수 있다.
정리
Importance-based Features : 각각의 노드가 그래프 전체에서 얼마나 중요한가?
- Node Degree
- Node Centrality
=> 그래프 전체에서의 해당 노드의 영향력을 예측할 때 유용(소셜 네트워크에서 유명인 예측)
Structure-based Features : 특정 노드 주변의 부분 그래프가 어떠한 위상학적 특징을 가지고 있는가.
- Node Degree
- Clustering Coefficient
- Graphlet Degree Vector
=> 특정 노드가 그래프에서 수행하는 역할에 대해 예측할 때 용이(단백질 상호작용 네트워크에서 특정 단백질의 역할 규명)
4. Link Prediction
지금까지 살펴본 Graph level prediction과 달리, link prediction은 두 노드 간의 관계에 집중한다. 즉, 지금의 그래프에서 모든 노드의 조합을 살피고, 그 중 상위 K 개의 조합을 최종 예측으로 산출하게 된다. 이를 위해선 변수로 두 노드의 조합을 생성하는 것이 중요하다.
가장 쉽게 생각할 수 있는 것은, 두 노드 변수를 단순하게 concat하는 것이다. 하지만 이는 두 노드의 정보를 담고 있지만, 두 노드의 관계를 정확하게 담고 있지 못하다. 그래서 주로 다른 방법들이 사용된다고 한다.
Link prediction을 접근하는 두가지 방법은 다음과 같다.
1. Links missing at Random
이미 존재하는 그래프에서 임의로 몇개의 링크를 지우고, 그 링크들을 예측하게 하는 것이다. 하지만, 이 경우 실제로 하고자 하는 태스크가 새로운 링크를 발견하고자 한다면, 훈련과 예측에서 다른 과정이 반복될 수 있다. 생명공학자들이 단백질 간의 관계를 새로 찾고자 하는 상황에서, 기존의 단백질 관계를 임의로 지우고 이를 예측하게 한다고 해서, 이것이 새로운 단백질 관계를 찾는데 도움이 된다는 보장이 없는 것이다.
2. Links over Time
그래프가 계속해서 변화하는 상황에서 사용하게 된다. 교통상황이나 소셜 네트워크와 같이 정적인 관계가 아닌 동적으로 계속 변화하는 관계를 예측할 때, time series prediction과 같이 작동하게 된다. 즉, 현재 시점의 그래프에서 다음 시점의 링크를 예측하고, 이를 다시 그 다음 시점의 예측에 사용하게 되는 것이다.
그렇다면 실제 모델링 과정을 살펴보도록 하자.
각각의 노드 쌍 (x, y)가 있을 때 다음과 같은 과정이 이루어진다.
1. 각 노드 쌍에 대한 임의의 점수 c(x, y)를 계산한다.
2. 모든 노드 쌍의 점수를 정렬한다.
3. 상위 K개의 쌍을 새로운 링크로 예측한다.
4. 실제 링크와 비교한다.
상당히 간단한 과정이다. 여기서 c(x, y)를 계산하는 과정에 따라 방법들이 달라진다는 것을 예측할 수 있는데, 이 수업에선 총 세개의 방법을 소개하고 있다.
4-1. Distance-Based Features
이 방법은 단순하게, 최소 거리를 점수로 사용하는 것이다.
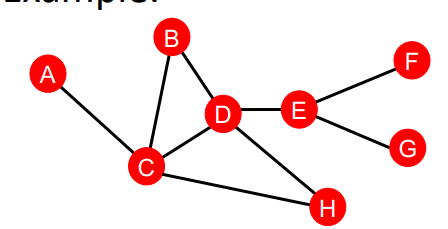
위 그래프에서 c(B, H) = 2가 된다. 또한 c(D, F) = 2가 된다. 하지만 점수가 나타내고자 하는 것이 두 노드가 연결된 강도임을 감안하면, (B, H) 쌍과 (D, F) 쌍의 점수가 동일한 것은 뭔가 석연치 않다. 누가봐도 B, H 조합이 좀 더 강하게 결합될 수 있는 것 같다. 이는 두 노드 간에 경로의 갯수와 관련이 있다고 할 수 있다. 둘 사이에 경로가 많고, 그 경로들이 짧기 때문이다.
4-2. Local Neighborhood Overlap
두 노드가 공통으로 가지고 있는 이웃을 고려하여 점수를 내는 방법엔 다음과 같은 것이 있다.
- Common Neighbors : 단순하게 두 노드가 공통으로 가지는 이웃 노드의 수이다.
- Jaccard's Coefficient : common neighbors를 두 노드의 이웃의 총합으로 정규화한 식이다.
- Adamic-Adar index : 두 노드가 공유하는 이웃 노드가 많을수록, 또한 그 이웃노드가 가진 이웃 노드(degree)가 적을수록 높은 점수를 부여하는 방법이다. 이웃노드가 적은 노드를 가지고 있는데, 두 노드가 포함된다는 의미는, 두 노드가 좀 더 밀접하다는 의미가 될 수 있기 때문이다.
하지만 이러한 Local neighborhood overlap에도 한계는 있다. 두 노드가 가지는 이웃노드만 살피다 보니, 두 노드의 거리가 3 이상이 되면 어떠한 경우에도 그 점수가 0이 된다는 것이다.
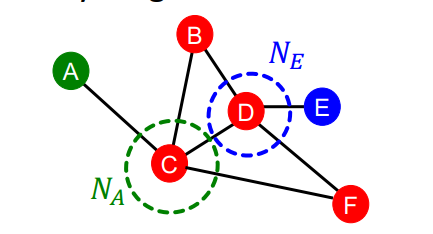
위의 그래프에서 A와 E는 거리가 3이지만, 관련성이 있을 수 있다. 하지만 local neighborhood overlap으론 이를 계산할 수 없다.
4-3. Global Neighborhood Overlap
그래서 좀 더 넓게 그래프를 보고 이웃 노드를 살피고자 Global neighborhood overlap이 있다. 이에 대해 이야기 하기에 앞서 Katz Index를 이야기 해야 한다.
Katz index : 주어진 두 노드 간의 모든 길이에 대해 경로의 수의 합
그렇다면 어떻게 길이가 3 이상일 때 경로의 수를 계산할 수 있을까? 놀랍게도 인접 행렬의 거듭제곱을 이용하면 된다.
노테이션을 잠시 짚고 넘어가자면 다음과 같다.
- if
- Let 길이가 K인 u와 v의 경로의 수
우리가 보이고자 하는 것은 이다.
우선 K = 1이면, 당연히도 참이다. 인접행렬의 의미가 u와 v의 엣지 존재 여부이니 말이다.
K=2이면, u -> i -> v로 경로를 분해할 수 있다. 즉, 가 된다.
그러면 i에 대한 summation을 적용하면 전체 과정이 종료된다.
결국 K가 3이상이더라도, 이와 같이 경로를 분해하면 동일한 과정이 되기 때문에 아래와 같이 성립한다.
이제 Katz index를 이용해 Global neighborhood overlap을 일반화해보자.
Global neighborhood overlap는 결국 길이가 1부터 무한대에 이르기까지의 Katz index의 합이다.
여기서 베타는 길이가 길어질수록 영향도를 줄이기 위한 discount factor이다.
위의 식을 closed-form으로 정리하면 다음과 같다.
짜잔! 우리는 이제 두 노드의 길이가 1부터 무한대에 이르기까지 모든 경로의 수를 더할 수 있게 되었다!
정리
Distance-based Features
- 두 노드 간 가장 짧은 거리를 사용하나, 이웃 노드의 정보가 활용되지 않음
Local Neighborhood Overlap
- 두 노드간 정보와 이웃 노드의 정보를 활용하나 길이가 3 이상인 노드 간 계산 불가
Global Neighborhood Overlap
- 두 노드간 거리에 관계없이 그래프 전체에 걸쳐 정보를 활용.
5. Graph Prediction
마지막으로 그래프 레벨에서의 예측 태스크를 알아보도록 하자.
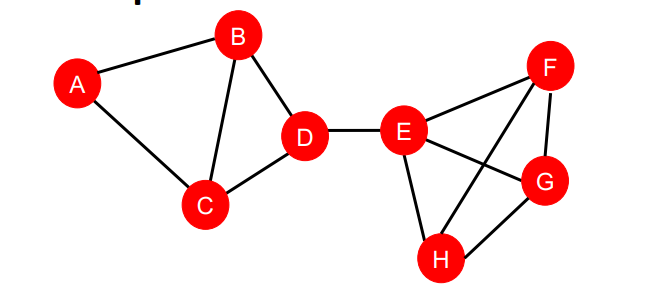
위의 그래프를 설명해보면 다음과 같다.
두개의 부분 그래프로 이루어져 있다. 각 부분 그래프는 일부 노드가 연결되어 있으며, 부분 그래프 간에는 하나의 엣지를 통해 연결되어 있다.
이러한 그래프에 대한 묘사를 어떻게 하면 변수화하여 사용할 수 있을지 고민하는 것이 그래프 레벨에서의 예측 태스크라고 할 수 있을 것이다.
5-1. Kernel Methods
이 때 사용하는 것이 커널은 다음과 같이 정의하고, 성질을 가지고 있다.
1. Kernel 은 데이터(그래프) 간의 유사도를 계산한다.
2. Kernel Matrix 은 항상 positive semidefinite한 행렬이다.
*positive semidefinite은 위키피디아에 나와있듯이, 항상 양의 실수를 아이겐벨류로 가진다.
3. 임의의 함수 는 feature vector를 생성하는 함수이며, 다음과 같이 정의된다.
4. 커널이 일단 정의되면, kernel SVM과 같은 다양한 ML 기법이 사용 가능하다.
5-2. Key Idea
커널을 이용하는 방법의 주요 목적은 그래프를 feature vecotr로 변환시켜주는 함수 를 설계하는 것이다.
이때 자연어 처리에서 사용하는 BoW(Bag of Words) 개념을 차용한다.
가장 단순하게는 모든 노드를 동일하게 보고, 노드의 갯수를 세면 된다.
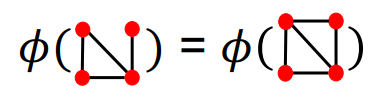
하지만 이런 방식은 그래프 구조가 달라도, 노드 갯수가 같으면 동일한 변수로 간주하기 때문에 좋지않은 방법이다.
여기서 한걸음 더 나아가면, Node Degree를 이용할 수 있다. 즉, node degree를 하나의 단어로 보고, node degree마다 빈도수를 세어 벡터화 하는 것이다.
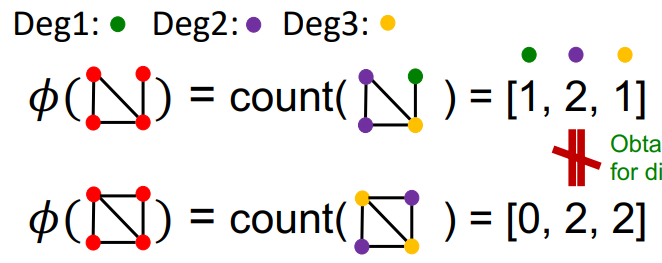
이를 통해 위와 같이 다른 구조의 그래프를 다르게 표현할 수 있게 된다.
물론 Node Degree를 사용하는 것 역시 너무 단순하고, 한계점이 있기 때문에, 이번 수업에서 배울 Grphlet Kernel과 Weisfeiler-Lehman Kernel(이하 WL Kernel) 모두 Bag-of-Something을 통해 를 정의한다.
5-3. Graphlet Kernel
Graphlet Kernel은 노드 레벨에서 봤던 그 graphlet을 이용하지만 조금 개념이 다르다. 두가지에서 다른데 다음과 같다.
- 모든 노드가 연결될 필요가 없다. 즉, 고립된 노드도 graphlet의 요소로 다룬다.
- 기준이 되는 노드를 설정하지 않는다.
예를 들어서 를 k의 크기를 가지는 graphlet의 리스트라고 할 때,
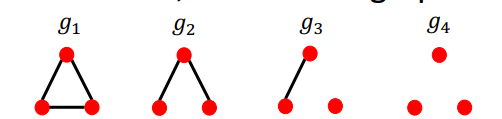
위와 같은 4개의 Graphlet을 가지게 된다.
즉, 어떤 그래프 G에 대해 graphlet list 은 Graphlet count vector인 를 정의하게 된다. 식으로 나타내면 다음과 같다.
예를 들어 K = 3일때 다음과 같은 그래프는 아래와 같이 를 가지게 된다.
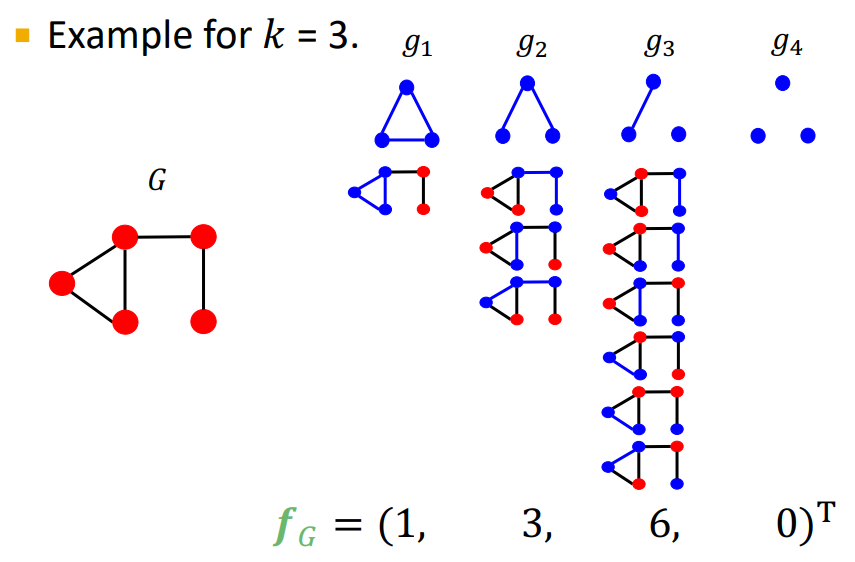
결국 graphlet kenel은 아래와 같이 계산되게 된다.
하지만, 이런 방식은 문제가 있다.
G와 G'의 크기가 다를 경우, 즉, 노드의 갯수가 다르게 되면 그 값이 왜곡되기 쉽다는 점이다. 우리는 두 그래프의 유사도를 측정하고 싶은건데, 단순히 한 그래프의 노드 수가 많다고 두 그래프가 비슷하지 않은 것은 아닐 것이다. 이를 보정하기 위해 정규화를 취해준다.
이렇게 되면 kenel함수 역시 조금 달라지게 된다.
하지만 Graphlet Kernel은 큰 단점이 있다.
매우 계산비용이 크다는 점이다. 만약 크기가 k인 graphlet을 크기가 n인 그래프에서 세고자 한다면, 이는 의 계산이 필요하다. 이를 효과적으로 줄이는 방법은 힘들다.
5-4. Weisfeiler-Lehman Kernel
WL Kernel은 다른 방법을 통해 을 효율적으로 만든다.
그 핵심 개념은 반복적으로 이웃 구조를 이용하여 노드 보캡을 구성하는 것이다. 즉, 앞서 언급한 Bog of Node Degrees를 일반화한 것이라 볼 수 있다. Bog of Node Degrees은 1-hop 이웃 정보만 활용하는 한계가 있어, 이를 개선한 것이다. 결국 우리는 가 효과적으로 그래프의 정보를 압축한 벡터만 뽑으면 되니 그 보캡이 효과적으로 정보를 압축하면서도 빠르게 계산할 수 있으면 되는 것이다.
그 방법은 다음과 같다.
- 그래프 G가 노드 집합 V로 이루어져 있을 때
- 초기 색 $c^{(0)}(v)를 각 노드 v에 배정한다.
- 다음 식을 이용해 반복적으로 색을 변화시킨다.
즉, 다음 색은 현재 노드 v의 색과 이웃노드 v의 색을 해쉬 함수를 이용해서 만들어지는 것이다.
이를 일정 수준 이상으로 반복하게 되면 은 K-hop만큼의 이웃에 대한 정보를 요약하게 된다.
예시를 통해 자세히 살펴보자.
-
Assign initial colors
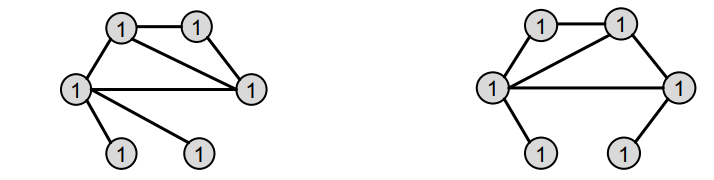
위 그림과 같이 두 그래프가 있다고 했을 때, 모두 동일한 색(1)로 배정한다. -
Aggregate neighboring colors

이웃 노드의 색을 concat하여 정보를 모은다. -
Hash aggregated colors

임의의 함수인 해쉬함수를 이용해 모은 정보를 하나의 색으로 변환한다. 이를 통해 현재는 1-hop에 해당하는 정보가 요약된 것을 알 수 있다. -
aggregate neighborring colors
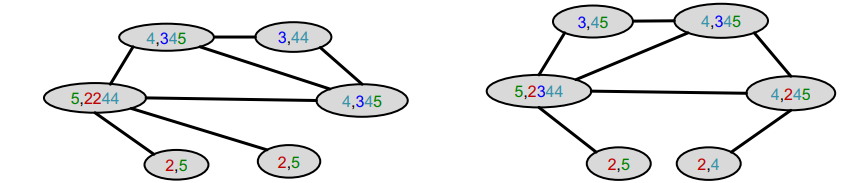
다시 이웃 노드의 색을 concat하여 정보를 모은다. -
Hash aggregated colors
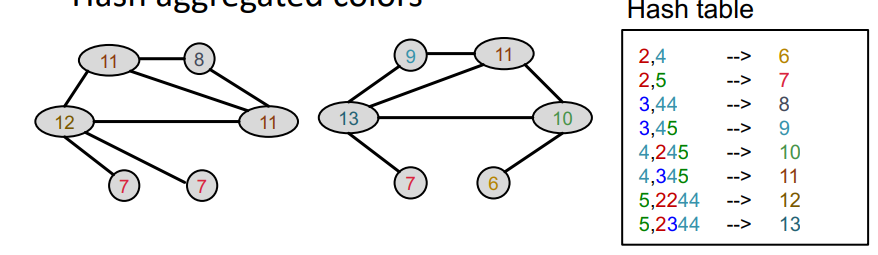
동일하게 해쉬함수를 이용해 모은 정보를 하나의 색으로 변환한다. 이를 통해 현재는 2-hop에 해당하는 정보가 요약된 것을 알 수 있다.
이 과정에서 중요한 것은 해쉬함수이다. 해쉬함수는 조금이라도 다른 입력값에 대해서는 전혀 다른 출력값을 반환하는 함수로서, 주변의 구조가 조금만 바뀌어도 다른 값을 반환하게 되는 것이다.
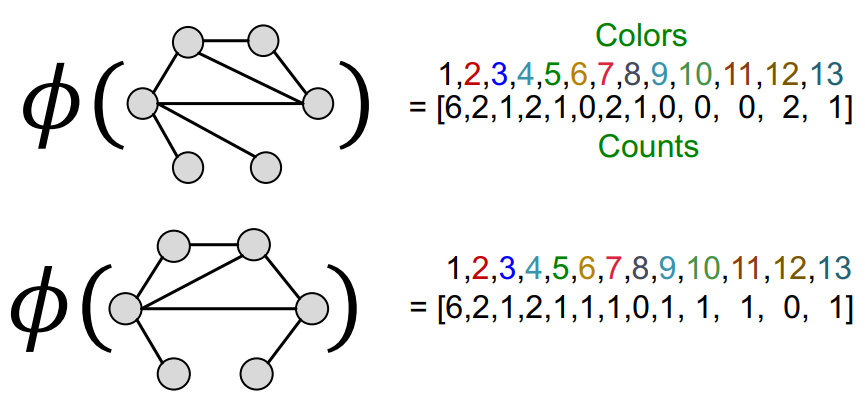
이렇게 변환된 색에 대한 결과를 벡터의 형태로 표현하면 함수가 완성된다. 여기선 K가 1, 2일때의 색을 표현하여 1-hop, 2-hop의 정보를 요약하여 나타낸 것임을 알 수 있다.
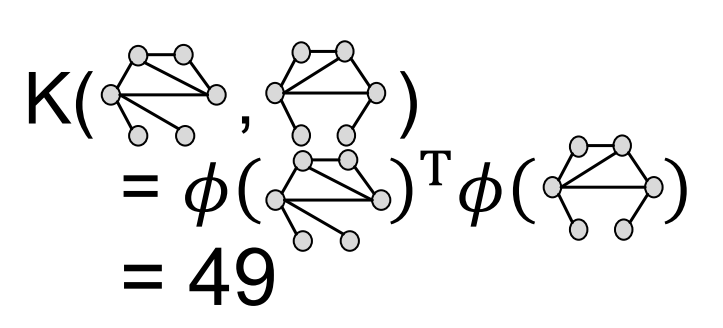
그리고 이러한 함수를 이용해 kernel을 구성하면 위와 같은 결과를 얻을 수 있다.
이런 방식을 이용한 WL Kernel은 엄청 빠르다는 장점이 있다.
- 색을 만드는 과정 : O(엣지의 수)
- 색의 갯수 : O(노드의 수)
- 색을 세는 과정 : O(노드의 수)
- 전체 과정 : O(엣지의 수)
위와 같이 모든 과정이 선형적인 시간 복잡도를 가지기 때문에, 사이즈가 큰 그래프에 대해서도 빠르게 연산이 가능하다.
정리
Graphlet Kernel
- 그래프는 bag-of-graphlet을 통해 표현된다.
- 시간복잡도가 매우 크다.
Weisfeiler-Lehman Kernel - K-스텝의 색 조합 알고리즘을 통해 노드의 색을 다양화한다.
- 그래프는 bag-of-colors를 통해 표현된다.
- 시간복잡도가 매우 작다.
- GNN과 매우 관련이 깊다.
참고
성균관대학교 이상구 교수님 연구실의 Perron-Frobenius 정리에 대한 설명
CS224W 강의자료
CS224W 2강
위키피디아

이해에 큰 도움이 되었습니다. 감사합니다!