Linear Classification

Linear classification (선형 분류)

문제 정의

입력–출력 : 데이터 (x,y)가 주어질 때, $x \in \mathbb{R}^d$ 로부터 분류 ID y를 예측

• 이진 분류: $y∈{0,1}$ (또는 $\{+1,−1\}$)
• 다중 분류: $y∈{0,1,…,N−1}$

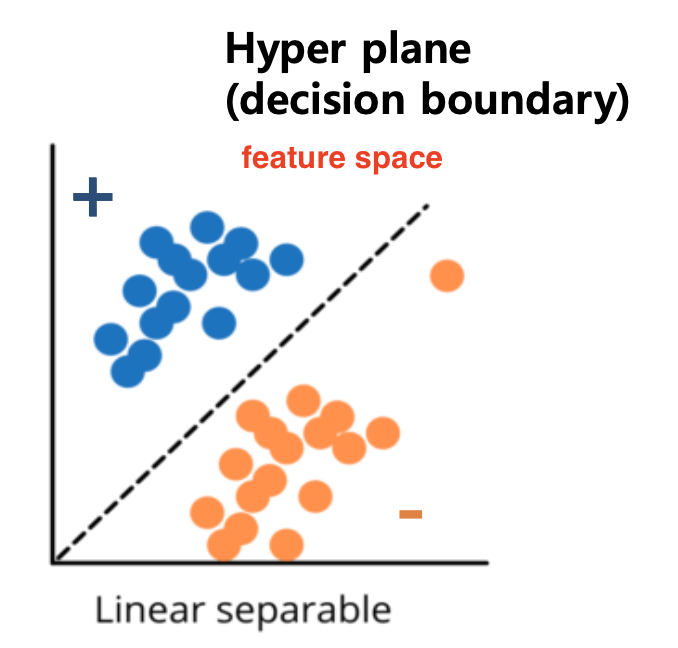
가설 집합 H: 초평면(Hyperplane)

선형 분류기는 결정 경계(decision boundary)를 Hyperplane으로 결정
Hyperplane을 기준으로 점들이 어느 쪽에 속하는지에 따라 레이블을 결정

선형 모델 표현

• 입력을 그대로 사용
  $h_w(x) = w_0 + w_1x_1 + \cdots + w_dx_d = w^T x$
  $w = (w_0, w_1, \ldots, w_d)^T$ : 학습되는 파라미터 벡터

• 특징 맵(feature map) 활용
  $h_w(x) = w_0 + w_1\phi_1(x) + \cdots + w_d\phi_d(x) = w^T \phi(x)$
  $\phi_j(x)$ : 비선형 함수를 씌운 새로운 특징

→ 고차원 특성 공간에서 비선형 결정 경계도 선형 모델로 학습 가능

Problem formulation

이진 분류 문제(binary classification) 를 수학적으로 나타내기

입력 공간 X 정의

d-차원 실수 공간을 입력 벡터의 집합으로 봄
ex. d=2라면 $x=(x_1,x_2)$ 형태의 2차원 좌표들이 모두 가능

출력 공간 Y 정의

두 가지 클래스를 +1, –1로 표시

목표 함수(target function) $f$

구현하고자 하는 이상적인 결정 규칙

가설(hypothesis) h와 가설 공간 $\mathcal{H}$

$\mathcal{H}$는 탐색(search) 가능한 함수들의 집합

Linear classification framework

선형 분류기(linear classifier)를 구성하는 요소

Hypothesis class (예측기 선택)

선형 결정 함수
$h(x) = \text{sign}(w_0 + w_1x_1 + \cdots + w_dx_d) = \text{sign}(w^T x)$

Loss function

• 0–1 손실 (Zero–one loss)
• Hinge loss
• Cross-entropy loss

Optimization algorithm (최적의 모델 파라미터를 찾는 방법)

경사 하강법 (Gradient Descent)

Linear classification model

예측 함수 h의 수식

$\sum_{i=1}^{d} w_i x_i$ 은 입력 x와 파라미터 w 간의 내적(dot product) 으로,
얼마나 + 쪽일지 vs − 쪽일지 판단하는 점수(score)를 줌

sign 함수의 역할

• z= $w^T x$가 양수면 +1 클래스
• z가 음수면 −1 클래스

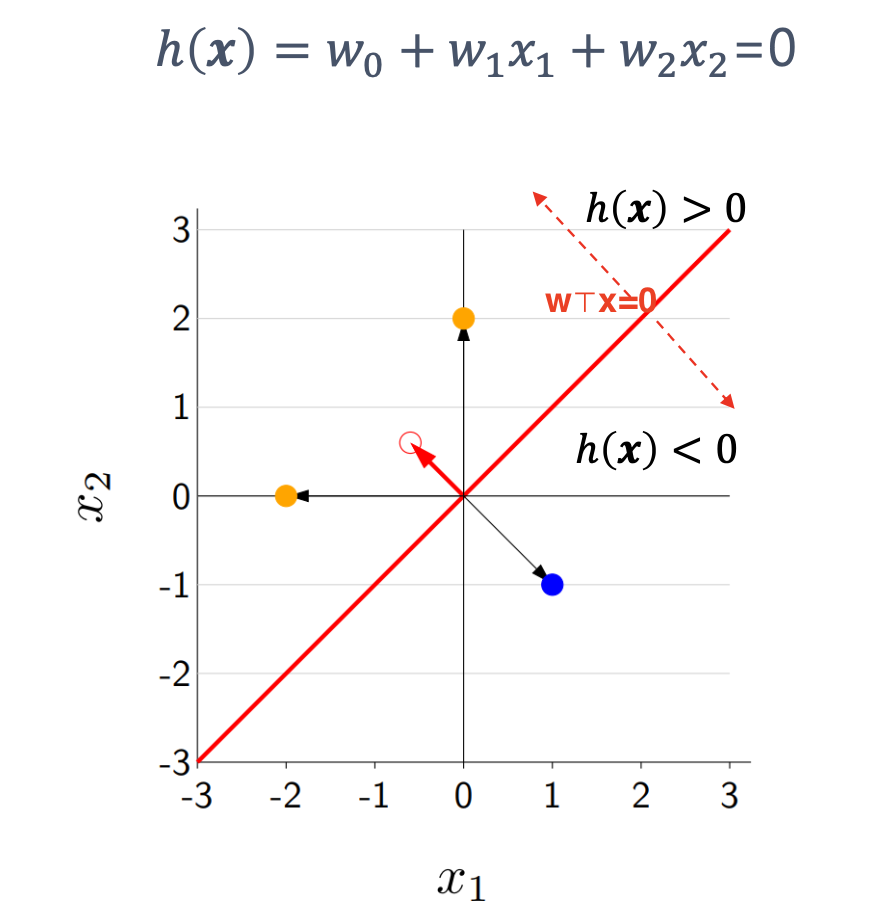
선 위쪽 영역: $w^T x>0$ ⇒ 예측값 +1
선 아래 영역: $w^T x<0$ ⇒ 예측값 -1

Example of linear classifier

모델 정의

• 파라미터 벡터

  $w = \begin{bmatrix} -1 \\ 1 \end{bmatrix}$

• 입력 특징 벡터

  $\phi(x) = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$

• 예측 함수

  $h(x) = \text{sign}(w^T \phi(x)) = \text{sign}(-1 \cdot x_1 + 1 \cdot x_2)$

점수(score) 계산 예시

Hypothesis class : which classifier?

두 가지 가설 클래스 비교

• 붉은 결정 경계

  $h_{w_{\text{red}}}(x) = \text{sign}([-1, 1] [x_1, x_2]^T) = \text{sign}(-x_1 + x_2)$

  결정 경계는 $x_2=x_1$ 직선

• 보라 결정 경계

  $h_{w_{\text{purple}}}(x) = \text{sign}([0.5, 1] [x_1, x_2]^T) = \text{sign}(0.5x_1 + x_2)$

  결정 경계는 $x_2=-0.5x_1$ 직선

0–1 손실 함수 정의

입력 x, 실제 y, 가중치 $w=[0.5,1]$ 일 때 $h_w(x)$ 계산

1. x=[0,2], y=+1,
   $h_w(x)=sign(0.5⋅0+1⋅2=2 >0)→ +1$
   → 정답, 손실 = 0

2. x=[1,-1], y=-1,
   $h_w(x)=sign(0.5⋅1+1⋅(-1)=-0.5 <0)→ -1$
   → 정답, 손실 = 0

Score and margin

선형 분류기에서 점수(score)와 여유도(margin)

Score(점수)

이 샘플이 +1 클래스일 확신도를 나타냄
s(x)>0 이면 모델은 +1,
s(x)<0 이면 –1 로 예측
→ s(x)값의 절댓값 ∣s(x)∣이 클수록 prediction에 더 confident

Margin(여유도)

예측이 올바른 정도를 수치화
ex.

• y=+1인데 $s(x) = w^T \phi(x)=5$ 면 margin = 5
  → 올바른(+1) 예측에 강한 여유가 있다

• y=+1인데 s(x)=−2 이면 margin = –2
  → 잘못(–1) 예측했고, 그 정도도 강하다(큰 음수)

기하학적 관점

margin은 (초평면에서부터의 거리) × (정답 부호) 로,

• 양수가 크면 “경계에서 멀리 떨어진 올바른” 샘플
• 음수가 크면 “경계에서 멀리 떨어진 잘못된” 샘플

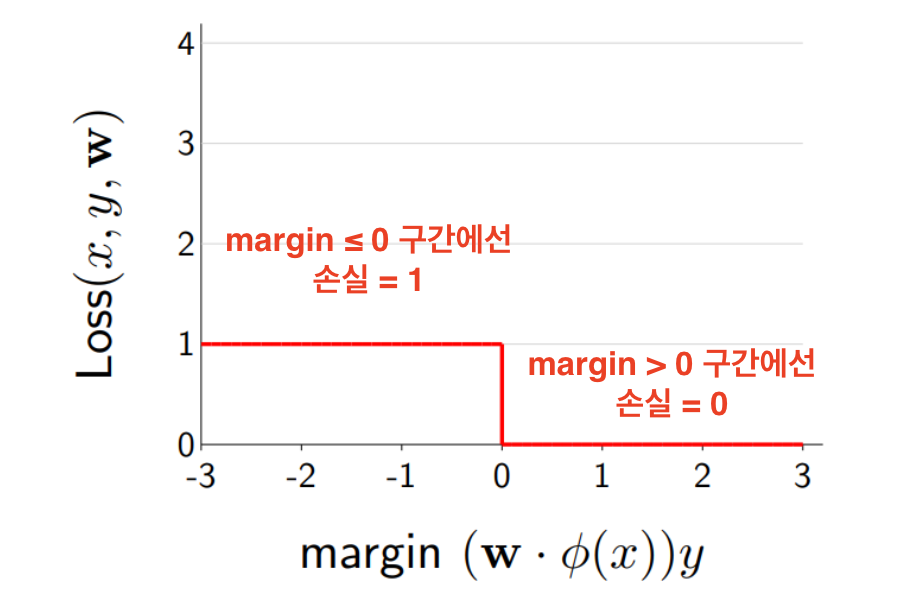
Zero-one loss

정의 : 맞음/틀림만 결정

틀렸으면 1, 맞혔으면 0

최적화 관점

Zero-one loss는

손실이 줄어드는 방향을 알려주는 기울기(gradient)가 거의 항상 0
→ 경사하강법이 전혀 동작하지 않음

Hinge loss

정의

margin $m=y (w^T \phi(x))$
m>0 이면 올바른 예측,
m<0 이면 오답

• m ≥ 1 일 때 Loss=0 (자신 있게 올바르게 분류)
• m < 1 일 때 Loss=1−m (거리에 비례해 선형 감소)

Hinge loss 사용 이유

Margin maximization
: 단순히 맞힌 여부(0–1)를 넘어서,
얼마만큼 경계에서 멀리 떨어져 올바른지(여유도)를 고려

경사하강법으로 최적화

경사하강법을 쓰려면 각 샘플에 대해
$\nabla_w \text{Loss}_{\text{hinge}}(x, y; w)$를 구해야함

• m<1 구간 (손실이 1−m인 구간)
  $\text{Loss}_{\text{hinge}} = 1 - y (w^T \phi(x)) \implies \nabla_w \text{Loss} = -y \phi(x)$

• m≥1 구간 (손실이 0인 구간)
  $\text{Loss}_{\text{hinge}} = 0 \implies \nabla_w \text{Loss} = 0$.
  이 샘플이 학습에 기여할 필요 없음

margin이 1 미만일 때만,
그 샘플이 내적 $w^T \phi(x)$ 방향으로 w를 당기도록 하는 역할
→ 전체 데이터에 반복 적용하면, 모든 샘플의 margin이 1 이상이 되도록 w가 학습

Cross-entropy loss

모델이 예측한 확률 분포 {q,1−q}와
실제(관측된) 분포 {p,1−p} 간의 크로스 엔트로피(Cross-entropy)

크로스 엔트로피 공식

→ 모델 예측 분포 q가 실제 분포 p와 얼마나 다른지 나타냄

Kullback–Leibler 발산과의 관계

KL 발산 $D_{\text{KL}}(p \| q)$ : 실제 분포 p와 모델 분포 q 간의 불일치 정도를 측정

→ 크로스 엔트로피 전체를 최소화 = $D_{\text{KL}}(p \| q)$를 최소화

Logistic Regression → classification

기존 linear models: Hard decision

입력 x를 직접 클래스 레이블 $y∈{+1,−1}$ 로 매핑

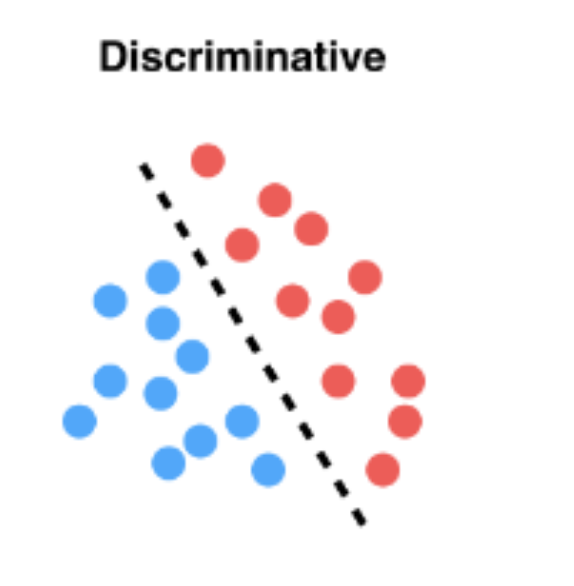
→ discriminative 모델

로지스틱 회귀 : Soft decision

입력→출력 매핑(판별적)이지만 확률을 출력
손실 함수로 크로스엔트로피(cross‐entropy loss) 사용

Probabilistic VS (Deterministic) discriminative function

확률적 판별 모델 (Probabilistic Discriminative)

주어진 입력 x 에 대해 샘플이 클래스 $C_k$ 에 속할 확률 $p(C_k | x)$을 예측

결정론적 판별 모델 (Deterministic Discriminative)

모델이 x라는 입력을 받으면 곧바로 $\{C_1, C_2, \ldots, C_K\}$ 중
하나의 클래스 레이블 $C_k$를 출력

Decision using a probabilistic model

문제

입력 x가 주어졌을 때
$y \in \{C_1, C_2\}$ 두 클래스 중 어디에 속하는지 예측

확률 기반 결정

확률 예측

x가 클래스 $C_K$ 일 사후 확률을 모델이 직접 계산

결정 규칙

확률이 더 큰 클래스를 고르는 최대 사후 확률(MAP) 방식

확률 예측을 위한 함수 설계 (Soft scoring)

점수(score) 계산

선형 모델로 점수 $z = w^T x$ 계산

로지스틱(시그모이드) 함수

점수 z 를 [0,1] 사이의 값으로 옮겨줌

• z≫0 이면 σ(z)≈1
• z≪0 이면 σ(z)≈0
• z=0 에서 σ(0)=0.5

Cf) Logistic regression VS Linear regression

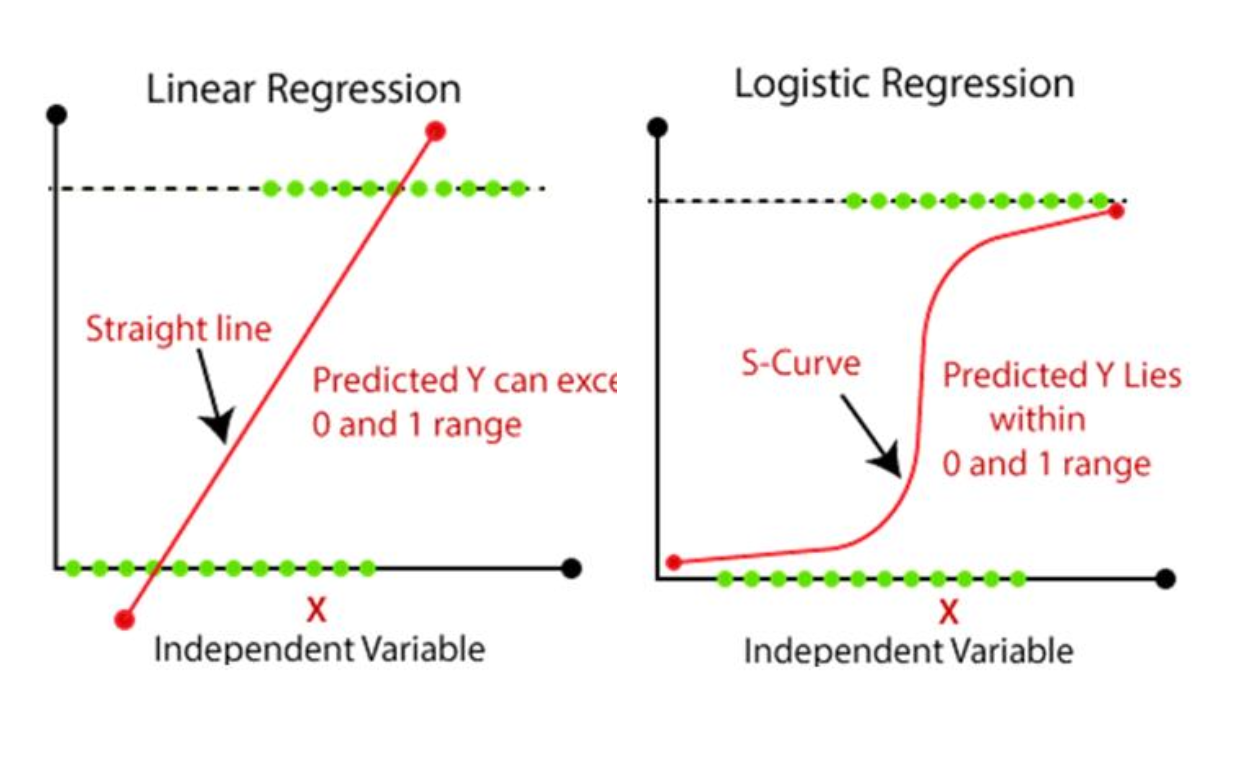
선형 회귀의 출력

연속적(continuous)이지만, 특별한 상한·하한(bound)이 없음
→ 분류에 바로 쓸 수 없음

로지스틱 회귀의 출력

시그모이드(s-curve) 형태로 부드럽게 연속적 값을 내지만,
항상 0과 1 사이로 제한(bounded)

Sigmoid function

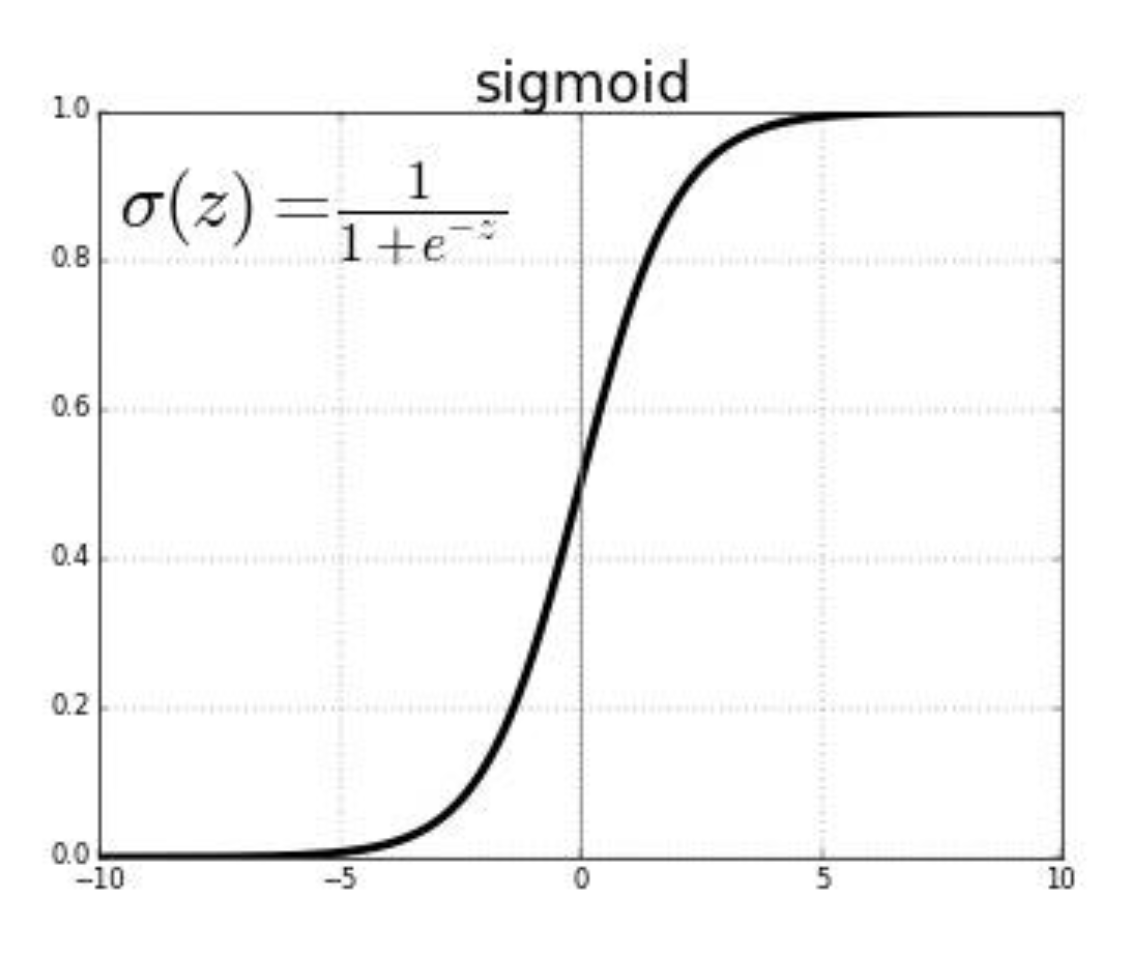
• 대칭성
  $σ(−s)=1−σ(s)$

• 중심값
  $\sigma(0) = \frac{1}{2}$

• 미분(기울기)
  → 최대 기울기는 $σ(0)=0.5$ 일 때, $σ'(0)=0.25$

선형 점수 → 시그모이드 로 스쿼시(squash)

확률 해석

x가 주어졌을 때 y=1일 사후 확률

x가 주어졌을 때 y=0일 사후 확률

→ 0–1 사이의 수치이므로 바로 확률로 사용 가능

Logistic Regression

그냥 linear regression

• 모델

  $h(x) = Wx + b \quad ( h(x) = W^T x)$

• Cost function
  평균제곱오차(MSE) 사용

  $\text{Cost}(W, b) = \frac{1}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})^2$

logistic regression

• 모델

  $h(x) = \sigma(W^T x + b) = \frac{1}{1 + e^{-(W^T x + b)}}$

• Cost function
  평균제곱오차를 그대로 쓰면, 비용 함수가 비볼록(non-convex) 이 되어
  → 경사하강법이 전역 최솟값을 보장하지 못함

→ new cost function required

Loss function for Linear Regression

엔트로피 H(X)의 정의

데이터가 얼마나 불확실한지를 측정

X는 확률변수,
$p_X(x)$는 확률변수 X가 값 x를 가질 확률.

크로스엔트로피 $H(p,q)$

실제 분포 p와 모델 분포 q 간 엔트로피를 측정

정보 이론(Information Theory) 에서 정의한 엔트로피(Entropy)
→ 머신러닝 분류 모델의 Loss 설계

Entropy

불확실성 측정:

• X가 여러 값으로 골고루 나타날수록(균등 분포) → 엔트로피 최대
• X가 한 값에 거의 확정적이면 → 엔트로피 0

$p_X(x)$ : 확률변수 $X$가 값 $x$를 가질 확률
$\log \frac{1}{p_X(x)}$ : 값 x가 발생할 때 얻는 정보량(비트 단위)

결합 엔트로피 (Joint Entropy)

확률변수 X와 Y를 한쌍 $(X,Y)$로 보고,
두 변수가 동시에 어떤 값을 가질 확률분포 $p_{X,Y}(x, y)$

→ 두 변수를 합쳐 하나의 큰 확률변수로 봤을 때의 전체 불확실성을 나타냄

조건부 엔트로피 (Conditional Entropy)

Y를 알았을 때 X가 여전히 가질 평균 불확실성

상호 정보량 (Mutual Information)

두 변수가 얼마나 서로 정보를 주고받는지(의존성·연관성)를 측정

H(X) : Y를 모를 때 X의 불확실성
H(X∣Y) : Y를 알았을 때 남는 X의 불확실성

Relative Entropy (K-L divergence)

두 확률분포 p와 q 사이의 거리(dissimilarity) 측정

KLD(상대 엔트로피) 정의

데이터의 실제 분포 p(x) 를 모델 분포 q(x) 로 근사하여 인코딩, 전송할 때
평균적으로 소비하는 추가 정보(비트)
→ p=q 이면 0

엔트로피·크로스엔트로피와의 관계

크로스엔트로피 $H(p, q)=\sum_{x \in {X}} p(x) \log \frac{1}{q(x)}$
엔트로피 $H(p)=\sum_{x \in {X}} p(x) \log \frac{1}{p(x)}$

따라서,

Cross-entropy loss

$\{p,1−p\}$ (실제 레이블 분포)와
$\{q,1−q\}$ (모델 예측 분포) 사이의 크로스엔트로피

크로스엔트로피 식

$p \log \frac{1}{q}$ : 실제 사건 발생 빈도 p만큼,
예측 확률 q을 쓸 때 드는 정보량(=손실)

${(1 - p) \log \frac{1}{1 - q}}$ : 사건 불발 빈도 1−p만큼,
불발 예측 확률 1−q을 쓸 때 드는 손실

→ 두 항을 더하면 모델 예측 확률 분포 {q,1−q}가 실제 분포
{p,1−p}를 얼마나 잘 근사하는가에 대한 평균 정보량(손실)

KL 발산과의 관계

크로스엔트로피 $H(p,q)$ 를 최소화하면,
상수인 H(p)를 제외하고 자동으로 ${D_{\text{KL}}(p \| q)}$ 최소화

로지스틱 회귀(Logistic Regression) 작동 방식

선형 점수 계산 (Score)

시그모이드로 확률 변환 (Sigmoid)

score을 0~1 사이 확률로 바꿈

크로스엔트로피 손실로 학습 (CE loss)

실제 레이블 $y∈{0,1}$와 예측 확률 $q$ 사이의
크로스엔트로피 함수를 손실로 사용

다중 클래스 예측에서 크로스-엔트로피 손실

예측 확률 벡터 $\bar{Y}$ 와 실제 레이블 L

$\bar{Y}$(estimated) : 모델이 소프트맥스 등을 통해 예측한 각 클래스의 확률 분포

$L$ (real): 실제 레이블을 원-핫(one-hot) 인코딩한 벡터
ex. 클래스 1이 정답 : L=[1,0,0]

크로스-엔트로피 손실 식

→ $L_i$가 1인 i번째 항만 살아남고, 나머지는 0이 되어 사라짐

계산 예시

정답 L=[1,0,0]

• $\bar{Y}=[1,0,0]$ (모델이 확신을 가지고 완벽히 맞춤)

  $\mathcal{L} = -[1 \cdot \log 1 + 0 \cdot \log 0 + 0 \cdot \log 0] = -\log 1 = 0$

  → 손실 0 (완벽)

• $\bar{Y}=[0,1,0]$ (모델이 완전히 틀림)

  $\mathcal{L} = -[1 \cdot \log 0 + 0 \cdot \log 1 + 0 \cdot \log 0] = -\log 0 = +\infty$

  → 손실 무한대 (매우 큰 패널티)

Learning target in logistic regression

클래스별 확률 정의

레이블 $y∈\{+1,−1\}$일 때 각각의 사후확률

하나로 합치기

시그모이드 성질 $1−σ(s)=σ(−s)$ 를 적용

Error for logistic regression

로지스틱 회귀에서 손실 함수(logistic loss)가 도출되는 방법

우도(likelihood) 최대화 관점

학습 데이터 $\{(x_n, y_n)\}_{n=1}^N$ 가 주어졌을 때,
모델이 각 샘플 $x_n$에서 실제 레이블 $y_n$를 맞출 확률

의 곱을 최대화(maximize)하려고 함
→ 확률을 곱하게 되면 값이 매우 작아져 0에 가까워짐

Negative Log-Likelihood

대신 로그를 취하고, 부호를 바꿔 minimize하는 관점으로 전환

로지스틱 손실(Logistic Loss) 식

$P(y_n | x_n) = \sigma(y_n w^T x_n)$을 대입하면

따라서 전체 학습 에너지(평균 손실)는

전체 평균 손실은

Training a logistic regression model

로지스틱 회귀 모델을 경사 하강법으로 학습하는 방법

가중치 초기화

t=0일 때 모델 파라미터 $w_0$ 를 무작위(또는 0 근처의 작은 값)로 설정

기울기(Gradient) 계산

현재 파라미터 $w_t$에 대한 손실 함수

에 대한 기울기(편미분)를 구함

이동 방향 결정

최솟값으로 가려면 손실의 증가 방향의 반대로 움직여야 함

파라미터 업데이트

Multiclass classification

세 개 이상(다중 클래스)을 한 번에 바로 처리할 수 없는 경우

One-vs-All

• 클래스 A 대 나머지(A vs not-A)로 하나의 이진 모델을 학습
• 클래스 B 대 나머지(B vs not-B)로 하나의 이진 모델을 학습
• 클래스 C 대 나머지(C vs not-C)로 하나의 이진 모델을 학습

예측 시에는 각 이진 모델이 내놓는

를 비교해 가장 높은 클래스로 결정

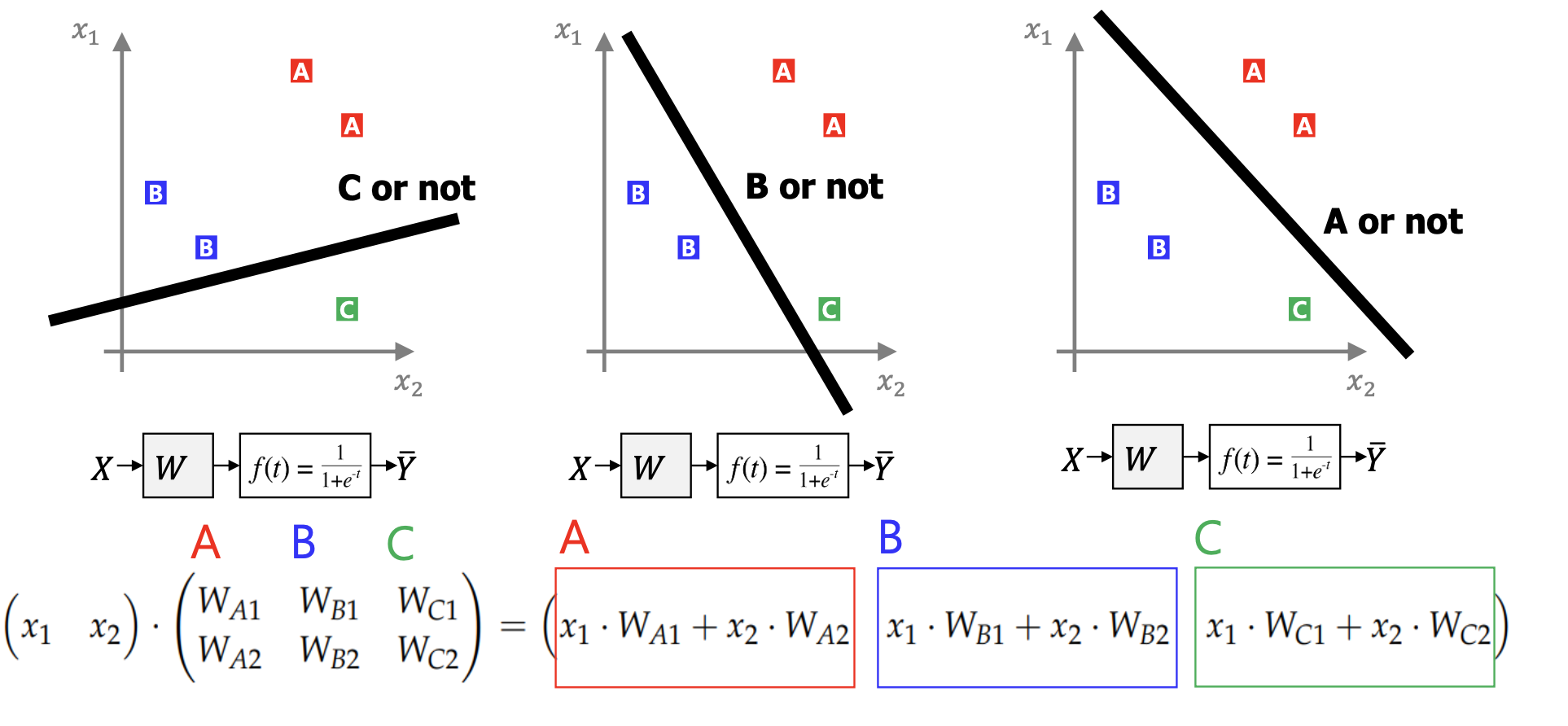
클래스별 이진 분류기

A vs not-A 이진 분류기의 선형 결정 경계 :

행렬곱으로 정리하기

입력 벡터 $x=(x_1,x_2)$ 를 가중치 행렬 W 와 곱하면

세 개의 스칼라 값이 각각
“A vs not”, “B vs not”, “C vs not” 분류기의 점수(score)

단점

다중 클래스 분류 - 마지막 출력층에 Softmax

선형 점수 계산

입력 벡터 x에 대해, 클래스 A,B,C 각각의 가중치 벡터를 내적해
선형 점수 $z_A, z_B, z_C$ 를 구함

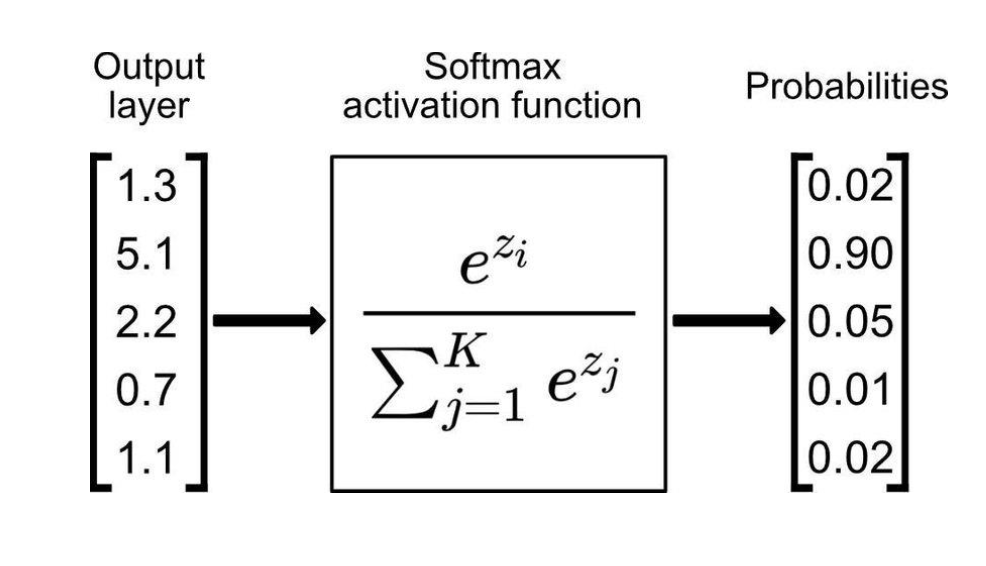
Softmax 활성화

구해진 점수 $z_i$ 를 Softmax 함수에 통과시키면,

로 확률 벡터 $(p_A, p_B, p_C)$를 얻음

Softmax의 특징:

• 모두 0~1 사이
• 합이 1

확률에 따른 최종 클래스

Softmax 결과 벡터를 얻으면
가장 높은 확률을 가진 인덱스를 골라 최종 예측을 내림

Wrap-up Logistic Regression

선형 스코어 $s = w^T x$

입력 벡터 x에 가중치 벡터 w를 내적해 스코어 s를 계산

시그모이드 함수 σ(s) → 확률 해석

시그모이드 함수를 씌우면 0~1 사이로 출력
= 샘플이 +1일 확률

소프트(threshold) vs 하드 분류

단순한 linear classification
: 스코어 s가 0 이상이냐 미만이냐에 따라 +1/−1로 hard하게 나눔

로지스틱 회귀
: 시그모이드를 거쳐 나오는 확률을
크로스엔트로피 같은 연속적 손실 함수로 측정하며,
최종 예측 시에도 h(x)>0.5를 기준으로 +1/−1을 결정하는 soft한 방식 사용

Advantage of linear classification

• 간단함 (Simple)
• 해석 가능성 (Interpretability)