Support Vector Machine

chelseey·2025년 4월 26일
MLL

Intuition: margin

margin : 어느 정도까지 허용하고도 제대로 분류할 수 있는 여유 공간

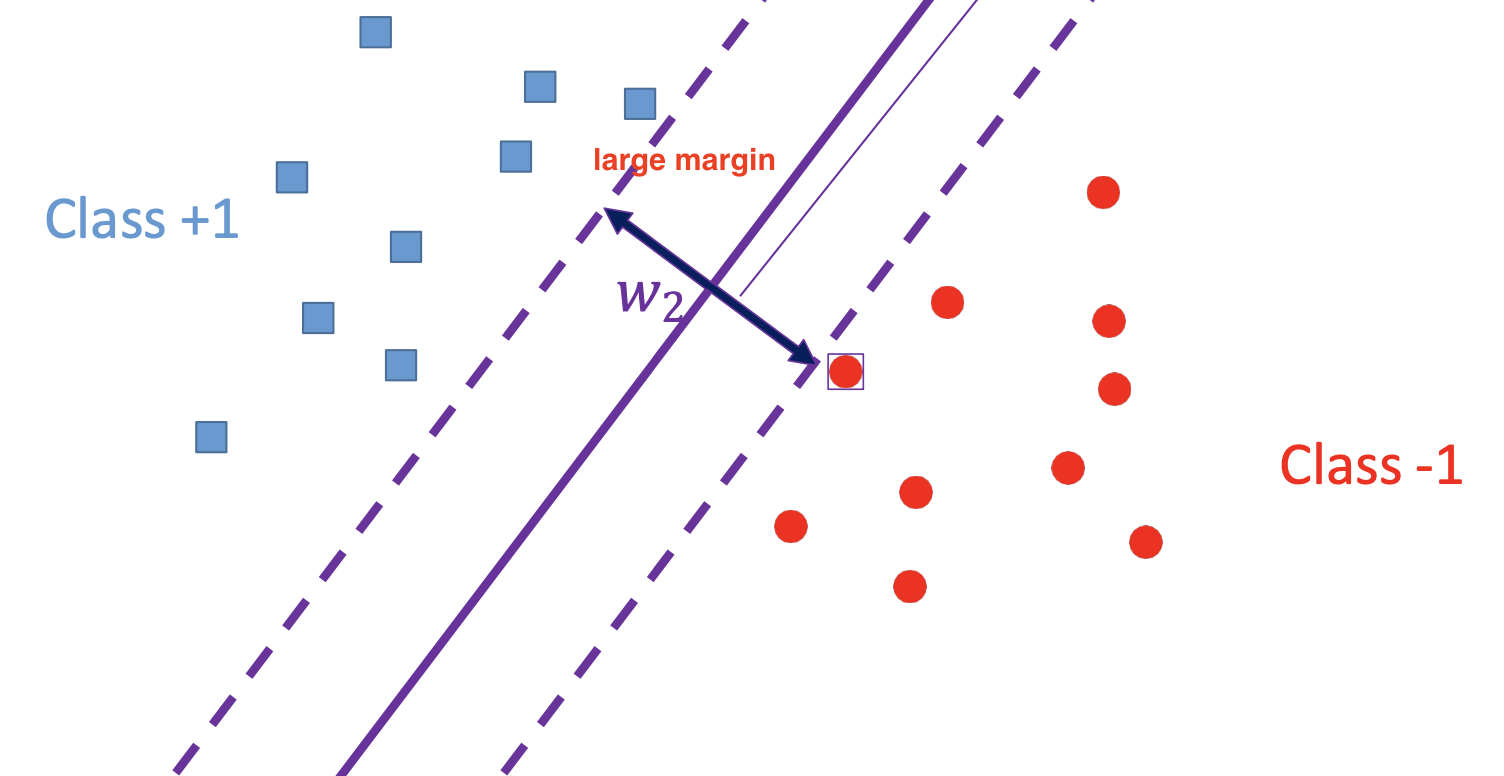
margin이 클수록 두 클래스의 “안전 영역”이 넓어져서,
새로운(시험) 데이터가 조금 이동해도 결정 경계 쪽으로 치우칠 가능성이 줄어들어
→ 일반화 성능이 좋아짐

Support Vector Machine

가장 넓은 margin을 주는(=가장 안정적인) 선형 경계를 찾아서 분류하고,
이 경계를 결정짓는 서포트 벡터들만
학습에 실제로 영향을 미치도록 설계된 모델

서포트 벡터(Support Vectors)

마진을 결정짓는(=경계에 가장 가까이 붙어 있는) 데이터 포인트

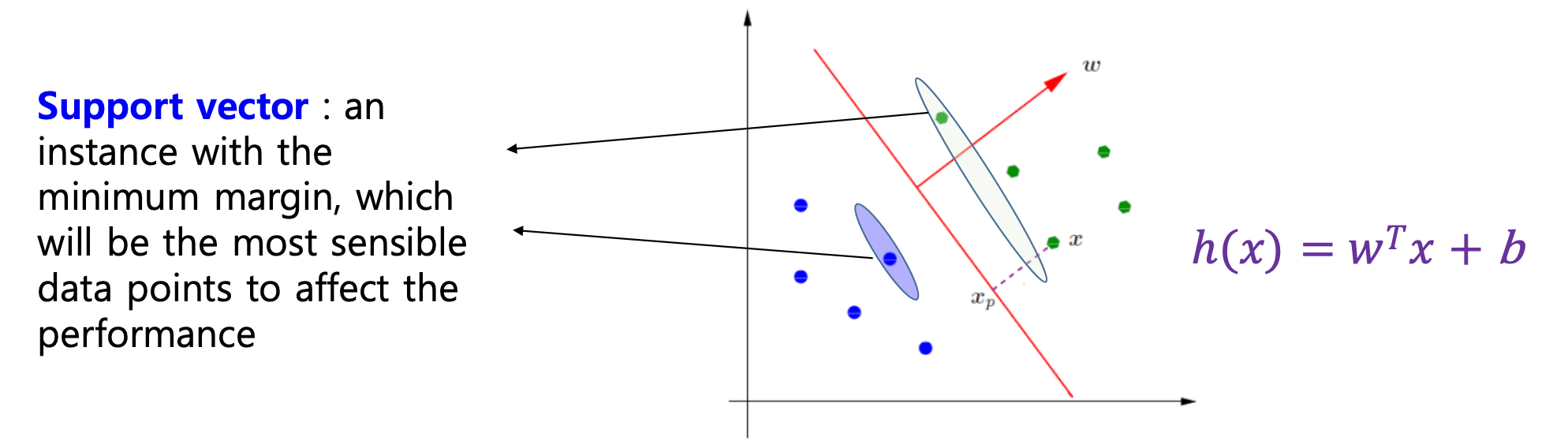
데이터 셋에 멀리 떨어진 노이즈나 이상치가 섞여 있어도,
그 포인트가 서포트 벡터 자리에 들어오지 않는 이상 경계를 바꾸지 않음
→ 모델이 이상치에 덜 민감해져서 robust(강건)

Margin

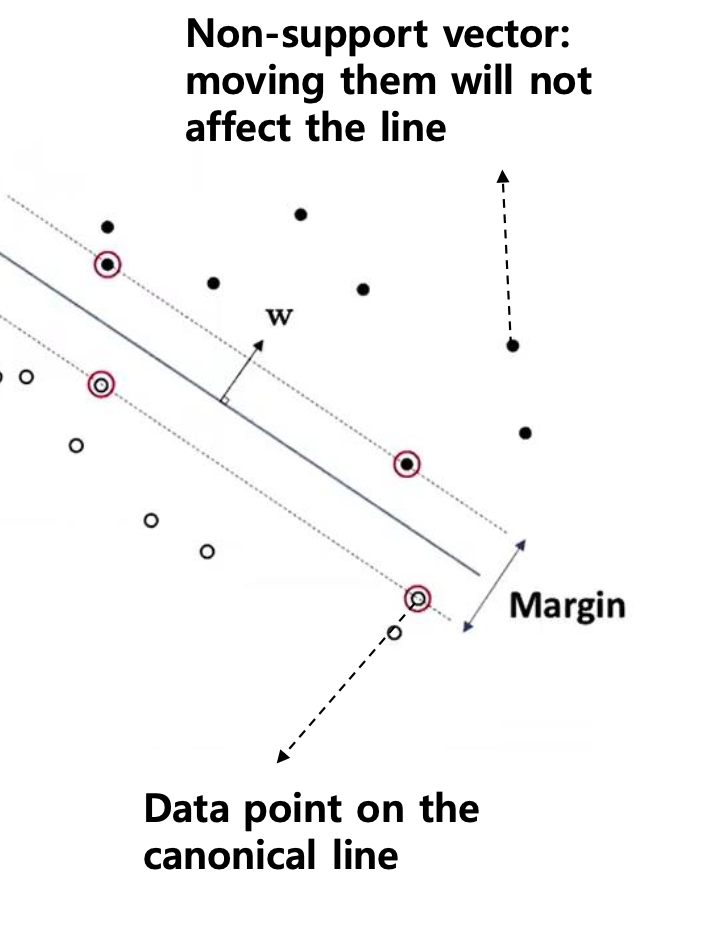
서포트 벡터

  • 위쪽 클래스(+1)에서 가장 가까운 점을 하나
  • 아래쪽 클래스(−1)에서 가장 가까운 점을 하나 선정

hyperplane ⇔ 서포트 벡터 간 거리

최적화가 잘 된 상태라면 :

  • 한쪽 서포트 벡터가 hyperplane으로부터 떨어진 거리 = d라고 하면,
  • 다른 쪽 서포트 벡터도 똑같이 d만큼 떨어져 있음

→ 마진(margin) = 2 × d

거리 공식

distance(x,hw,b(x)=0)=∣wTx+b∣∥w∥\text{distance}(x, h_{w,b}(x) = 0) = \frac{|w^T x + b|}{\|w\|}

: hw,b(x)=wTx+b=0h_{w,b}(x) = w^T x + b=0인 hyperplane에서
어떤 점 xx가 떨어진 수직 거리

→ 두 클래스의 서포트 벡터들은 이 거리가 가장 작은 점들이고,
SVM은 이 최소 거리를 최대화 하도록 w,b 를 학습

Margin distance

어느 한 점 x가 hw,b(x)=wTx+b=0h_{w,b}(x) = w^T x + b=0인 hyperplane에서
얼마나 떨어져 있는지를 보여주기 위한 증명

점 x 를 두 부분으로 분해하기

x⊥ : 주어진 점 x에서 hyperplane으로 수직으로 내렸을 때 닿는 점
w∥w∥\frac{w}{\|w\|} : hyperplane의 법선(수직) 방향 단위벡터
r : x⊥로부터 x 까지 hyperplane에 수직으로 이동한 거리

x=x⊥+rw∥w∥x = x_\perp + r \frac{w}{\|w\|}

양변에 wTw^T를 곱하고 b를 더하기

wTx+b=wT(x⊥+rw∥w∥)+b=(wTx⊥+b)+rwTw∥w∥w^T x + b = w^T \left( x_\perp + r \frac{w}{\|w\|} \right) + b = (w^T x_\perp + b) + r \frac{w^T w}{\|w\|}

rwTw∥w∥=r∥w∥2∥w∥=r∥w∥r \frac{w^T w}{\|w\|} = r \frac{\|w\|^2}{\|w\|} = r \|w\| 이므로,

hw,b(x)=wTx+b=0+r∥w∥=r∥w∥h_{w,b}(x) = w^T x + b = 0 + r \|w\| = r \|w\|

거리 공식

∣wTx+b∣∥w∥\frac{|w^T x + b|}{\|w\|}

Optimization

모든 점을 올바르게 분류하면서, 두 클래스 간 margin을 최대화하는
최적의 w와 b를 찾는 방법

선형분리가 안 될 때 → 커널 트릭

현실 세계 데이터는 완벽히 선형분리가 어렵기 때문에,
비선형 특징 변환 ϕ(x)ϕ(x)를 한 뒤
내적을 ϕ(x)Tϕ(x′)\phi(x)^T \phi(x') 대신 커널 함수 K(x,x′)K(x,x')로 계산하여
고차원 공간에서는 선형 분리가 가능하도록 만들어줌

Support vectors

서포트 벡터와 정규화

하이퍼플레인(결정경계) : hw,b(x)=wTx+bh_{w,b}(x) = w^T x + b
margin 계산을 편하게 하기 위해
서포트 벡터에 대해 h(x)=±1h(x)=±1이 되도록 w,b 스케일을 정규화

ex. 어떤 점 xtx_t가 클래스 +1 쪽 가장 가까이 붙어 있다고 하면,
h(xt)=+1h(x_t)=+1이 되도록 w,b를 전체적으로 늘이거나 줄임

거리 공식 유도

서포트 벡터는 wTx+b=±1w^T x + b=±1이므로
support vector 거리 =∣±1∣∥w∥=1∥w∥= \frac{|\pm 1|}{\|w\|} = \frac{1}{\|w\|}

margin=1∥w∥−(−1∥w∥)=2∥w∥\text{margin} = \frac{1}{\|w\|} - \left(-\frac{1}{\|w\|}\right) = \frac{2}{\|w\|}

constraints: linearly separable

클래스별 경계식

  • y=+1은

    h(x)=wTx+b≥+1h(x) = w^T x + b \geq +1

    실선 위쪽 영역에 있어야 하고

  • y=−1은

    h(x)=wTx+b≤−1h(x) = w^T x + b \leq -1

    실선 아래쪽 영역에 있어야 함

따라서,

yn×(wTxn+b)≥1y_n × (w^T x_n + b) \geq 1

objective function

마진을 크게 ⇔ ∥w∥∥w∥을 작게

거리를 최대화하려면 2∥w∥\frac{2}{\|w\|}를 키워야 하고,
이는 결국 ∥w∥∥w∥을 최소화하는 것과 동일

→ ∥w∥2∥w∥^2 최소화

최종 SVM Primal 문제

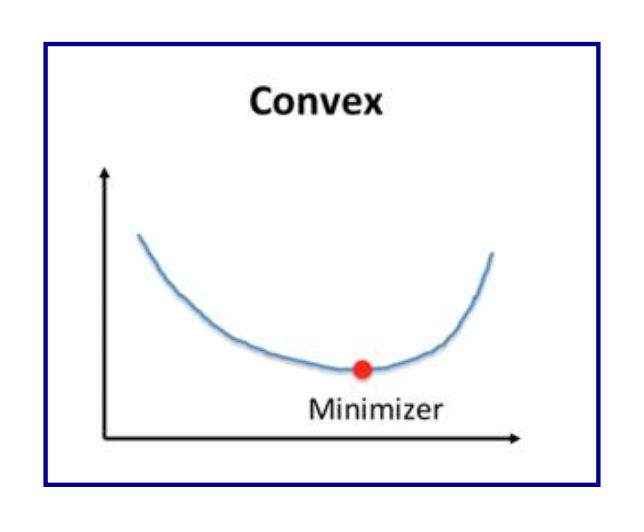
min⁡w,b∥w∥2subject toyi(wTxi+b)≥1(∀i)\min_{w,b} \|w\|^2 \quad \text{subject to} \quad y_i (w^T x_i + b) \geq 1 \quad (\forall i)

convex optimization

목적 함수가 2차(quadratic) 형태

min⁡w,b∥w∥2\min_{w,b} \|w\|^2

제약 조건이 선형(linear) 형태

yi(wTxi+b)≥1for all samples iy_i (w^T x_i + b) \geq 1 \quad \text{for all samples } i

부등식은 w와 b에 관해 linear

→ convex quadratic programming 문제, 전역 최적해가 보장

Primal and Dual problem for understanding SVM

SVM 최적화를 풀기 위해
primal problem → dual problem 로 바꾸는 과정

제약이 있는 일반적 최적화 문제

min⁡wf(w)s.t.{gi(w)≤0,i=1,…,K(부등식 제약)hj(w)=0,j=1,…,L(등식 제약)\min_{w} f(w) \quad \text{s.t.} \quad \begin{cases} g_i(w) \leq 0, & i = 1, \ldots, K \quad (\text{부등식 제약}) \\ h_j(w) = 0, & j = 1, \ldots, L \quad (\text{등식 제약}) \end{cases}

→ 이 상태로는 부등식 제약 + 등식 제약을 그대로 다루면서
w만 최적화해야 해서 풀기가 까다로움

라그랑지안(Lagrangian) 도입

제약(부등/등식)을 목적 함수 안으로 옮겨오기 위해
Lagrange multipliers αi,βjα_i,β_j 를 도입

L(w,α,β)=f(w)+∑i=1Kαigi(w)+∑j=1Lβjhj(w)L(w, \alpha, \beta) = f(w) + \sum_{i=1}^{K} \alpha_i g_i(w) + \sum_{j=1}^{L} \beta_j h_j(w)

Dual Problem (이중 문제)

  • Primal Problem (원래 문제) : P∗=min⁡wmax⁡α≥0,βL(w,α,β)P^∗=\min_{w} \max_{\alpha \geq 0, \beta} L(w, \alpha, \beta)

  • Dual Problem : d∗=max⁡α,βmin⁡wL(w,α,β)d^* = \max_{\alpha, \beta} \min_{w} L(w, \alpha, \beta)

볼록(convex)한 문제라면 Strong Duality가 성립해 두 값이 같음

→ Dual 문제만 풀어도 Primal 해 w∗w^∗를 구할 수 있음

KKT 조건 (Karush–Kuhn–Tucker)

Primal과 Dual의 해 w∗w^∗와 α∗α^∗,β∗β^∗는
다음 네 가지 조건을 모두 만족해야만 최적해가 됨

  • ∇wL(w∗,α∗,β∗)=0\nabla_w L(w^*, \alpha^*, \beta^*) = 0
  • gi(w∗)≤0,hj(w∗)=0g_i(w^*) \leq 0, \quad h_j(w^*) = 0
  • α∗≥0α^∗≥0
  • αi∗gi(w∗)=0\alpha_i^* g_i(w^*) = 0

→ 네 가지를 만족할 때에만
Strong Duality, 두 문제의 해가 일치

Optimization objective function

Primal 문제: 제약 있는 최적화

min⁡w,bJ(w)=∥w∥2\min_{w,b} J(w) = \|w\|^2
s.t. yi(wTxi+b)≥1,i=1,…,Ny_i (w^T x_i + b) \geq 1, \quad i = 1, \ldots, N

마진(margin) ∥w∥2\|w\|^2를 최소화하면서
모든 샘플 (xi,yix_i,y_i)이 hyperplane로부터 최소 1 이상 떨어지도록

Dual 문제로 전환: Lagrangian 도입

L(w,b,α)=∥w∥2+∑i=1Nαi[1−yi(wTxi+b)]L(w, b, \alpha) = \|w\|^2 + \sum_{i=1}^{N} \alpha_i [1 - y_i (w^T x_i + b)]

Solving a dual problem

라그랑지안 정류 조건(Stationarity)

라그랑지안 함수 L(w,b,α)를 실제로 최적화하려면
w와 b에 대해 기울기(편미분)가 0이 되어야 함

L(w,b,α)=∥w∥2+∑i=1Nαi[1−yi(wTxi+b)]L(w, b, \alpha) = \|w\|^2 + \sum_{i=1}^{N} \alpha_i [1 - y_i (w^T x_i + b)]

를 w와 b에 대해 편미분하여 0으로 놓으면 :

∂L∂w=0  ⟹  w=∑i=1Nαiyixi\frac{\partial L}{\partial w} = 0 \implies w = \sum_{i=1}^{N} \alpha_i y_i x_i

→ 1. 최적 w는 샘플 벡터의 선형 결합

∂L∂b=0  ⟹  ∑i=1Nαiyi=0\frac{\partial L}{\partial b} = 0 \implies \sum_{i=1}^{N} \alpha_i y_i = 0

→ 2. αiα_i는 레이블 yiy_i 합이 0이 되도록 분포

Primal 변수 w,bw,b 제거

1번, 2번 식을 원래 Lagrangian에 대입해
w항은 ∑i=1Nαiyixi\sum_{i=1}^{N} \alpha_i y_i x_i 으로 바꾸고
b항은 ∑i=1Nαiyi=0\sum_{i=1}^{N} \alpha_i y_i = 0 으로 반영해서 제거

정리하면,

L(α)=∑i=1Nαi−12∑i=1N∑j=1Nαiαjyiyj(xiTxj)L(\alpha) = \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i^T x_j)

subject to

αi≥0,∑i=1Nαiyi=0\alpha_i \geq 0, \sum_{i=1}^{N} \alpha_i y_i = 0

Convex Quadratic Programming(QP)

SVM Dual 문제는
일반적인 Convex Quadratic Programming(QP) 문제의 한 예

일반 QP 문제의 형태

목표

min⁡x12xTPx+qTx\min_{x} \frac{1}{2} x^T P x + q^T x

제약

Ax=b,Gx≤hA x = b, \quad G x \leq h

SVM Dual ↔ QP 대응

max⁡α∑i=1Nαi−12∑i=1N∑j=1Nαiαjyiyj(xiTxj),\max_{\alpha} \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i^T x_j),

s.t.

∑i=1Nαiyi=0,αi≥0(∀i)\sum_{i=1}^{N} \alpha_i y_i = 0, \quad \alpha_i \geq 0 \quad (\forall i)

  • 목표식

    max⁡α[1Tα−12αTHα]⟺min⁡α12αTHα−1Tα\max_{\alpha} \left[ \mathbf{1}^T \alpha - \frac{1}{2} \alpha^T H \alpha \right] \quad \Longleftrightarrow \quad \min_{\alpha} \frac{1}{2} \alpha^T H \alpha - \mathbf{1}^T \alpha

  • H 행렬의 구성

    Hij=yiyj(xiTxj)H_{ij} = y_i y_j (x_i^T x_j)

→ 표준 QP 포맷으로 SVM Dual을 풀 수 있음

Final solution

QP가 내놓은 최적의 αi∗α_i^∗ 값을 바탕으로, SVM의 최종 해인
w∗w^∗,b∗b^∗ 를 구하는 과정

가중치 벡터 w∗w^∗

QP 솔버가 반환한 αi∗α_i^∗ 중 0이 아닌 것(=서포트 벡터)에 대해서만 더함

편향(bias) b∗b^∗

서포트 벡터 중 하나를 골라, 결정 경계 조건

w∗Tx++b∗=+1,w∗Tx−+b∗=−1w^{*T} x_+ + b^* = +1, \quad w^{*T} x_- + b^* = -1

을 평균내면 편향이 구해짐

b∗=−12(w∗Tx++w∗Tx−)b^* = -\frac{1}{2} (w^{*T} x_+ + w^{*T} x_-)

예측 함수 h(x)

최종 분류기는

h(x)=sign(w∗Tx+b∗)=sign(∑i=1Nαi∗yixiTx+b∗)h(x) = \text{sign}(w^{*T} x + b^*) = \text{sign}\left(\sum_{i=1}^{N} \alpha_i^* y_i x_i^T x + b^*\right)

Example (in 2D)

2차원 공간에 3개의 샘플이 있을 때
SVM의 듀얼 문제를 풀어서 w와 b를 구하기

예제에서 주어진 xix_i와 yiy_i

입력 벡터

x1=(10),x2=(01),x3=(02)x_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad x_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \quad x_3 = \begin{pmatrix} 0 \\ 2 \end{pmatrix}

레이블

y1=+1,y2=−1,y3=−1y_1 = +1, \quad y_2 = -1, \quad y_3 = -1

입력 내적(Gram) 행렬 Kij=xiTxjK_{ij} = x_i^T x_j

K=(100012024)K = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 2 \\ 0 & 2 & 4 \end{pmatrix}

H 행렬 : Hij=yiyjKijH_{ij} = y_i y_j K_{ij}

H=((+1)(+1)1(+1)(−1)0(+1)(−1)0(−1)(+1)0(−1)(−1)1(−1)(−1)2(−1)(+1)0(−1)(−1)2(−1)(−1)4)=(100012024)H = \begin{pmatrix} (+1)(+1)1 & (+1)(-1)0 & (+1)(-1)0 \\ (-1)(+1)0 & (-1)(-1)1 & (-1)(-1)2 \\ (-1)(+1)0 & (-1)(-1)2 & (-1)(-1)4 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 2 \\ 0 & 2 & 4 \end{pmatrix}

dual 목적함수

J(α)=∑i=13αi−12[α1,α2,α3][100012024][α1α2α3]J(\alpha) = \sum_{i=1}^{3} \alpha_i - \frac{1}{2} [\alpha_1, \alpha_2, \alpha_3] \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 2 \\ 0 & 2 & 4 \end{bmatrix} \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{bmatrix}
=α1+α2+α3−[0.5α12+0.5α22+2α32+2α2α3]= \alpha_1 + \alpha_2 + \alpha_3 - [0.5\alpha_1^2 + 0.5\alpha_2^2 + 2\alpha_3^2 + 2\alpha_2\alpha_3]

제약조건

제약조건 ∑i=13αiyi=0\sum_{i=1}^{3} \alpha_i y_i = 0

(+1)α1+(−1)α2+(−1)α3=0  ⟹  α1−α2−α3=0(+1) \alpha_1 + (-1) \alpha_2 + (-1) \alpha_3 = 0 \implies \boxed{\alpha_1 - \alpha_2 - \alpha_3 = 0}

부등식 제약

α1≥0,α2≥0,α3≥0\alpha_1 \geq 0, \quad \alpha_2 \geq 0, \quad \alpha_3 \geq 0

최적조건(편미분)

목적함수 J(α₁,α₂,α₃)의 최적점을 찾기 위해
변수 α₁, α₂, α₃에 대해 편미분(∂J/∂αᵢ)을 모두 0으로 놓음

{1−α1=0,1−α2−2α3=0,1−2α2−4α3=0.\begin{cases} 1 - \alpha_1 = 0, \\ 1 - \alpha_2 - 2\alpha_3 = 0, \\ 1 - 2\alpha_2 - 4\alpha_3 = 0. \end{cases}

α1−α2−α3=0\alpha_1 - \alpha_2 - \alpha_3 = 0 과 풀면

α1=1,α2=1,α3=0\alpha_1 = 1, \quad \alpha_2 = 1, \quad \alpha_3 = 0

w와 b 복원

가중치 벡터 ww

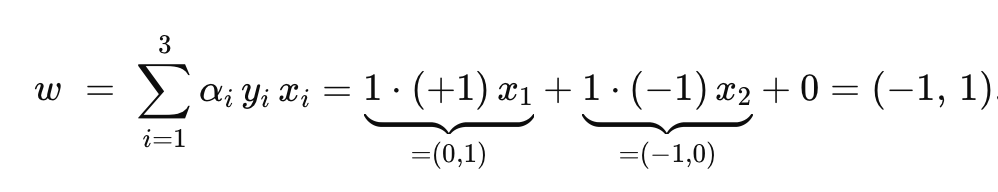
bias bb
서포트 벡터로 (0,1) (양성) 과 (1,0) (음성)을 고르면 :
w∗Tx++b=+1w^{*T} x_+ + b = +1
w∗Tx−+b=−1w^{*T} x_- + b = -1

b+=1−wT(0,1)=1−(−1⋅0+1⋅1)=1−1=0b_+= 1 - w^T (0, 1) = 1 - (-1 \cdot 0 + 1 \cdot 1) = 1 - 1 = 0
b−=−1−wT(1,0)=−1−(−1⋅1+1⋅0)=−1−(−1)=0b_-=-1 - w^T (1, 0) = -1 - (-1 \cdot 1 + 1 \cdot 0) = -1 - (-1) = 0

두 값을 평균 내 주면 b=0b=0

최종 분류함수

h(x)=sign(wTx+b)=sign(−1⋅x1+1⋅x2)h(x) = \text{sign}(w^T x + b) = \text{sign}(-1 \cdot x_1 + 1 \cdot x_2)

Properties of dual variable 𝜶

Lagrangian multipliers 𝛼

SVM의 듀얼 문제를 세울 때, 각 훈련 샘플 i 마다 하나씩 도입됨
비음수여야 함. αiα_i≥0

서포트 벡터와 비서포트 벡터

  • 서포트 벡터(Support Vector)
    αi>0α_i>0 인 샘플들만 최종 결정 경계를 결정하는 데 기여
    Margin 경계에 걸려 있어서 yi(wTxi+b)=1y_i (w^T x_i + b) = 1 만족

  • 비서포트 벡터(Non–Support Vector)
    αi=0α_i=0인 샘플들
    yi(wTxi+b)>1y_i (w^T x_i + b) > 1 인 영역에 있어서 경계 결정에 전혀 영향을 주지 않음

결정 계수 w 의 표현

w=∑i=1Nαiyixi=∑i:αi>0αiyixiw = \sum_{i=1}^{N} \alpha_i y_i x_i = \sum_{i: \alpha_i > 0} \alpha_i y_i x_i

0인 αiα_i들은 합에 기여하지 않으므로
실제로는 서포트 벡터들만으로 w 를 구성

Drawbacks of SVM

원래 입력 공간에서는 서로 섞여 있어서
선형(직선·평면)으로 분리할 수 없는 데이터를 다루는 방법

원래 입력 공간에서 비선형 모델을 쓰는 방법

결정 트리나 신경망처럼
복잡한 경계(곡선·곡면)를 학습하는 분류기를 쓰는 방법

커널 트릭(kernel-trick)

입력을 더 높은 차원의 공간으로 변환한 뒤(=특징 변환),
그 공간에서 선형 모델을 사용

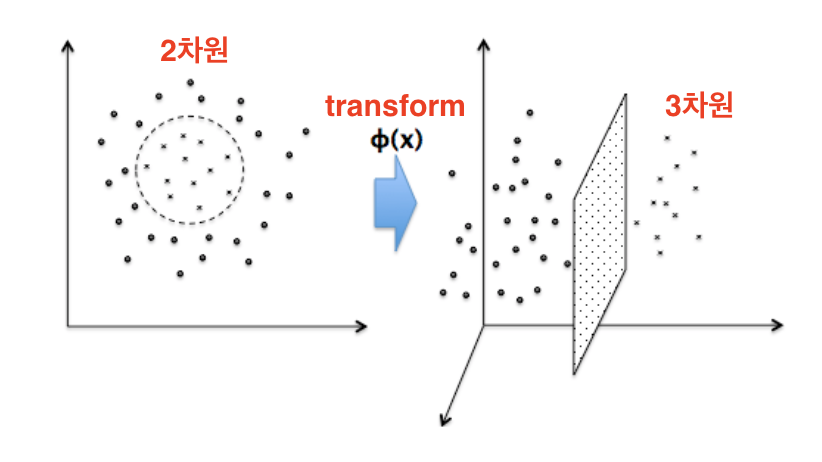
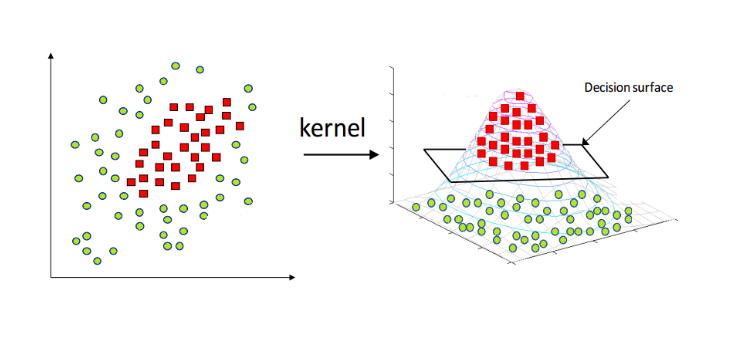
  • 원형 영역 안팎으로 구분된 데이터는
    2D 입력 평면상에서 원 하나로는 분리할 수 없지만,
  • ϕ(x)ϕ(x) 라는 함수로 3차원으로 transform하면
  • 3D 공간의 하나의 평면으로는 나눌 수 있음

Linearity in linear models

비선형 입력을 쓰고 싶을 때

x가 복잡해서 직선·평면으로 분리할 수 없는 경우
원래 x 대신 ϕ(x)ϕ(x)처럼 고차원·비선형 특징을 새로 만들어 사용

선형성은 w에 대해서만 유지됨

모델을

f(x)=wTx⟶f(x)=wTϕ(x)f(x) = w^T x \quad \longrightarrow \quad f(x) = w^T \phi(x)

바꿔도, 파라미터 w에 대해서는 여전히 linear하기 때문에

  • 목적 함수는 여전히 볼록이고
  • 경사(gradient), Lagrange multiplier를 구할 수 있음

Transform

비선형 변환 φ:X→Z,φ:X→Z,

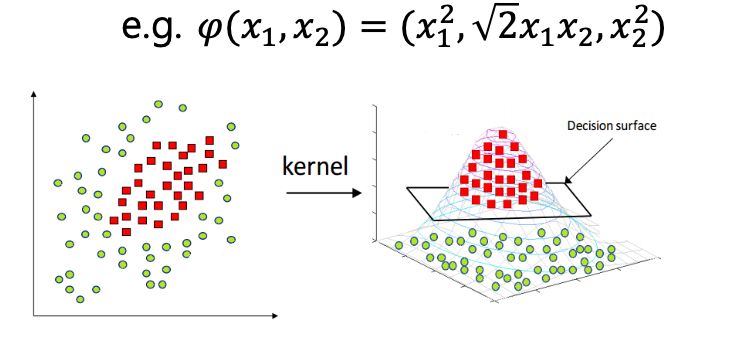
x∈X⟼z=φ(x)∈Zx \in \mathcal{X} \quad \longmapsto \quad z = \varphi(x) \in \mathcal{Z}

Z\mathcal{Z}는 X\mathcal{X}보다 차원이 높음

원래 (x1,x2x_1,x_2) 평면에서 원형·타원형 경계가
Z에서는 평면 하나로 분리됨

복잡한 경계 → 고차원에서 선형

Some thoughts

SVM의 dual 목적함수

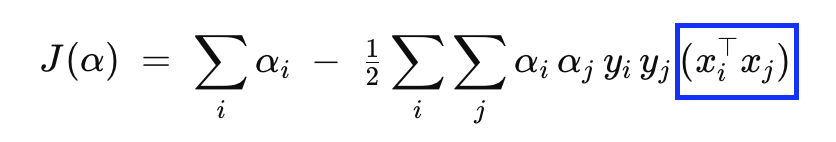
(xiTxj)(x_i^T x_j)만이 실제 입력 벡터의 차원 d 에 따라 달라지는 부분

고차원 맵 φ(x)φ(x)을 만들면 계산·메모리 비용이 큼

Kernel

저 차원의 벡터를 받아서, 고차원 공간에서의 내적값만 돌려주는 함수

SVM dual 형태에서는 내적 φ(xa)⋅φ(xb)φ(x^a)⋅φ(x^b) 만이 필요하고,
이는 커널 함수 K(xa,xb)K(x^a, x^b)로 대체할 수 있음

φ(xa)⋅φ(xb)=(a12,2a1a2,a22)⋅(b12,2b1b2,b22)=a12b12+(2a1a2)(2b1b2)+a22b22=a12b12+2a1a2b1b2+a22b22=(a1b1+a2b2)2=(xa⋅xb)2.\begin{aligned} \varphi(x^a) \cdot \varphi(x^b) &= (a_1^2, \sqrt{2} a_1 a_2, a_2^2) \cdot (b_1^2, \sqrt{2} b_1 b_2, b_2^2) \\ &= a_1^2 b_1^2 + (\sqrt{2} a_1 a_2)(\sqrt{2} b_1 b_2) + a_2^2 b_2^2 \\ &= a_1^2 b_1^2 + 2 a_1 a_2 b_1 b_2 + a_2^2 b_2^2 \\ &= (a_1 b_1 + a_2 b_2)^2 \\ &= (x^a \cdot x^b)^2. \end{aligned}

→ 3차원 사영 후의 복잡한 내적을
원래 2차원 점의 내적의 제곱 (xa⋅xb)2(x^a \cdot x^b)^2으로 대체

SVM dual 목적함수에서

∑i∑jαiαjyiyj(φ(xi)⋅φ(xj))\sum_{i} \sum_{j} \alpha_i \alpha_j y_i y_j (\varphi(x^i) \cdot \varphi(x^j))

대신

∑i∑jαiαjyiyj(xi⋅xj)2\sum_{i} \sum_{j} \alpha_i \alpha_j y_i y_j (x^i \cdot x^j)^2

커널 함수 K는 특징 공간 내적을 원래 입력에 대한 함수로서 계산할 수 있게 해 줌

K(x,x′)=⟨φ(x),φ(x′)⟩,K:Rd×Rd→RK(x, x') = \langle \varphi(x), \varphi(x') \rangle, \quad K : \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}

Some commonly used kernels

다항식 커널 (Polynomial Kernel)

입력 벡터 x,y의 내적에 상수 1을 더한 뒤, p차로 올려줌

K(x,y)=(x⋅y+1)pK(x, y) = (x \cdot y + 1)^{\color{red}p}

파라미터
p: 다항식 차수

가우시안 RBF 커널 (Gaussian Radial Basis Function)

두 점 사이의 유클리드 거리를 지수 함수로 감쇠(decay)시켜,
가까운 점에 높은 값을, 먼 점에 낮은 값을 줌

K(x,y)=exp⁡(−∥x−y∥22σ2)K(x, y) = \exp\left(-\frac{\|x-y\|^2}{2{\color{red}\sigma}^2}\right)

파라미터
σ: 반경을 조절.
σ가 작으면 국소적(local) 영향이 강해지고, 크면 더 넓게 부드럽게 퍼짐

시그모이드 커널 (Hyperbolic Tangent / MLP Kernel)

다층 퍼셉트론(neural network)의 은닉층 활성화 함수처럼,
입력 내적을 tanh로 통과시킴

K(x,y)=tanh⁡(k(x⋅y)−δ)K(x, y) = \tanh({\color{red}k}(x \cdot y) - {\color{red}\delta})

파라미터
k: 입력 내적의 스케일
δ: 편향(bias) 역할

Radial-basis function (RBF) kernel

K(x,x′)=exp⁡(−γ∥x−x′∥2)K(x, x') = \exp(-\gamma \|x - x'\|^2)
  • 점 x와 x′가 가까울수록 ∥x−x′∥∥x−x'∥가 작아지고, K는 1에 근접.
  • 멀어질수록 K는 0에 수렴.

γ : RBF의 폭. 값이 클수록 '좁고 날카로운' 가우시안 곡선

  • 큰 γ: 유사도가 급격히 줄어들어 국소적인(very local) 결정경계
    → 과적합 위험

  • 작은 γ: 부드러운 곡선 → 모델이 충분히 비선형성을 포착 못 함(underfit)

Performance

SVM의 장점

  • 다양한 분야(ex. 이미지, 텍스트)에서 일관되게 좋은 결과를 보여줌

  • 자동화된 학습 절차
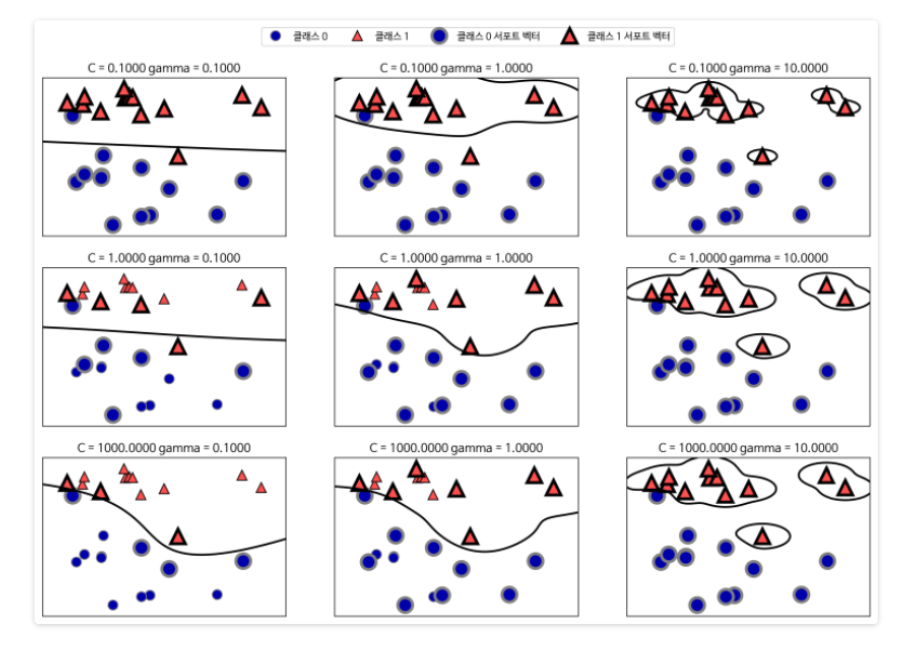
    적절한 커널 함수와 그 하이퍼파라미터(C, γ 등)만 선택하면,
    Decision boundary 학습은 QP로 자동 수행

  • 유연한 구조 가정
    데이터의 분포나 경계 형태에 대한 사전 지식이 거의 없어도,
    커널 트릭을 통해 비선형 경계를 효과적으로 학습

SVM의 단점

  • 시간·공간 복잡도
    학습 비용이 훈련 샘플 개수 N의 제곱에 비례 (O(N2), O(N3))(O(N^2),~O(N^3))하여, 데이터셋이 커지면 메모리·연산량이 급격히 늘어남

  • 모델 저장 비용
    결정 경계를 표현하는 서포트 벡터(αi>0α_i>0인 샘플)를
    모두 저장해야 하기 때문에,
    서포트 벡터가 많으면 예측 시에도 메모리·계산이 많이 듦

profile
chelseey
이전 포스트

Linear Classification

다음 포스트

Random forest

0개의 댓글