boolean
-
bool = 1바이트 정수
-
왜 정수 시간에 안다뤘나
-
-> 일리 있음 어셈블리에서 bool이라는 것은 없음
-
참/거짓 둘중 하나라는 힌트를 준다 => "가독성"
c++은 어셈블리보다 하이레벨 언어
왜 1비트로 안 쓸까? ❗

여기서 이거 한칸만 쓰는데...
어셈블리 시간에서
레지스터도
al 과 같은 최소 연산 단위가 다 1바이트였다.
울며겨자 먹기로 bool도 1바이트씀.
실수
공속 = 1초당 공격횟수
-
float : 4byte -> float a = 123.123f;
-
double : 8byte -> double b = 123.123;
(어제 __int64도 8바이트)
float 를 사용할 때는 f 붙여야한다.
실수 표현 ❗
쩜을 기준으로 16/16 비트씩 끊어서 표현을 할까??
=> 표현할 수 있는 가짓수가 줄어든다.
=> 그다지 좋은 방법 아님.
그래서 결국 실수를 표현을 할 때에는
"부동 소소점" 을 이용하게된다.
부동 소수점
"부동" == 안 움직임. 이 부동의 뜻이 아님.
뜰 "부" 소수점이 둥둥 떠다니면서 움직인다.
즉, .을 유동적으로 움직여서 표현하는 방법
예시 ❗❗
3.141592 를 표현해야한다고 가정을 하면은
3.141592 = 0.3141592 10 = 314.1592 10^-2
이런식으로 표현이 가능하다.
양식 정하기(정규화)
10진수를 기준으로 보면은
0.3141592 10 이게 정규화 된 것이라( 10 이 있어서) 대표로 오고
정규화 = 0.3141592 * 10
-
3141592 = 유효숫자
-
1 (=10) = 지수 (몇승을 곱했는지)
이게 부동 소수점의 핵심 이다.
부동소수점에서의 비트
-
float : 부호 1비트, 지수 8비트, 유효숫자 23비트 => 32비트
-
double : 부호 1비트, 지수 11비트, 유효숫자 52비트 => 64비트
부동 소수점 계산 방법
-3.375라는 값을 저장한다면
-
- 2진수로 변환해야함 => 3 + 0.375
3은 0b11 +
- 2진수로 변환해야함 => 3 + 0.375
-
- 0.375를 2진수로 변환
1을 기준으로 오른쪽에 가상의 숫자들이 있다고 생각하면 된다.
오른쪽으로 1칸 가면 0.5를 담당한다. (== 2^-1)
오른쪽으로 2칸 가면 0.25를 담당 (== 2^-2)
- 0.375를 2진수로 변환
2배씩 줄어듦
0.375 = 0.5 0 + 0.25 1 + 0.125 * 1 로 이루어진 숫자이다.
여기서 0, 1, * 1 을 추출을 하면은 2진수 표현법이 된다.
=> 0.375 = 0b0.011 이 최종적으로 나온다.
그래서 최종적으로
0b11 + 0b0.011 => 0b11.011 이라는 숫자가 나옴 (2진수 값. 우리가 원하는 값)
2진수로 구하고 정규화
0b11.011 이것을 정규화를 하면 0b1'1'.011 에서 1을
0b1.'1'011 로 옮긴다.
2진수에서의 정규화 기준은 . 쩜을 기준으로 앞에 있는 것이 1이라면 정규화 승자이다.
0b1.1011 * 2^1 (곱하기 2를 해주어야 0b11.011 와 똑같이 나옴)
그러면 부호는 마이너스라서 1로 켜주면되고 1bit
지수는 2^1 이라 1로 켜주면되고 1bit
11011 + 11011 => 11100 => 11110 => 11110 => 100110 => 110110
0b1.1011 = 110110
유효 숫자 1011 (쩜 뒤에 숫자)
단, 지수는 unsigned byte라고 가정을 하고 숫자 127을 더해서 만들어준다.

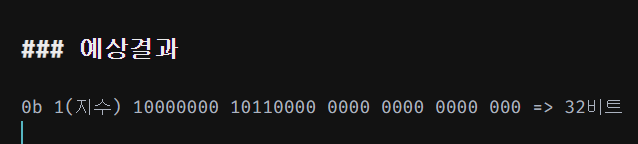
예상결과
0b 1(지수) 10000000 10110000 0000 0000 0000 000 => 32비트
주소값 -> 메모리
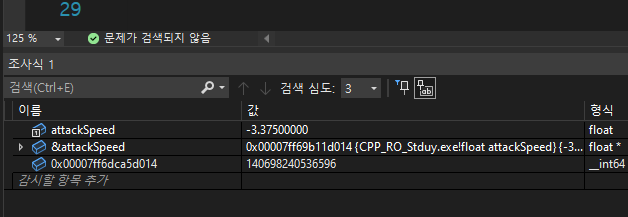
attackSpeed라는 값을 조사식에 치고
-3.375
이것에 & 주소를 출력한다음에
메모리에 쳐보도록 하자
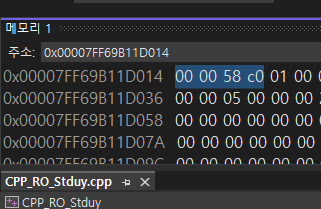
여기 4바이트가 attackSpeed의 값이다.
그런데 little endian이라
뒤집어서 봐야함
따라서 0xc0580000
계산기로 보면은
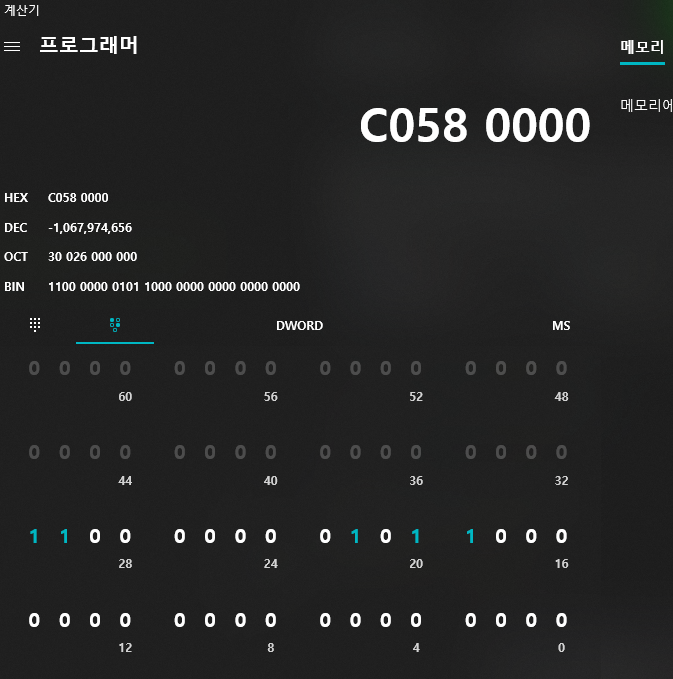
이런값이다.
1100 0000 0101 1000 0000 0000 0000 0000
1 1000 0000 1011 0000 0000 0000 0000 ...
똑같다.
기억해야 할것❗
-
프로그래밍을 할 때 부동소수점은 항상 '근사값' 이라는 것을 기억하자
-
실수 두개를 ==으로 비교하는 것은 지양하자.

