
이진트리
완전 이진 트리'
"힙"이라는 자료구조를 만들 때 쓴다.
자식을 항상 꽉꽉 채운 이진트리
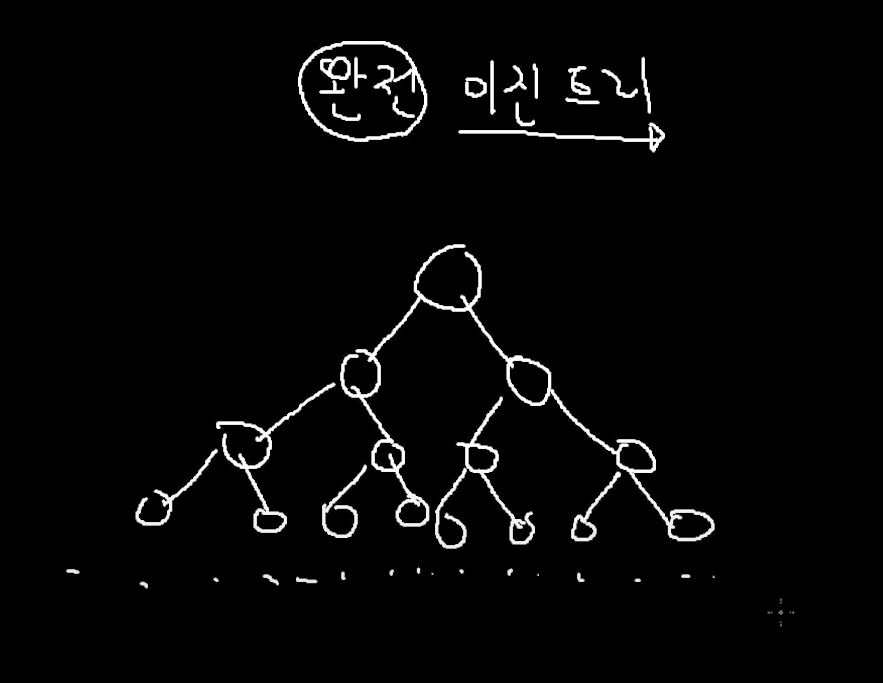
이런 규칙을 가지는 트리는
일반적으로 "배열"로 구현을 한다.
자식노드 ❗❗❗
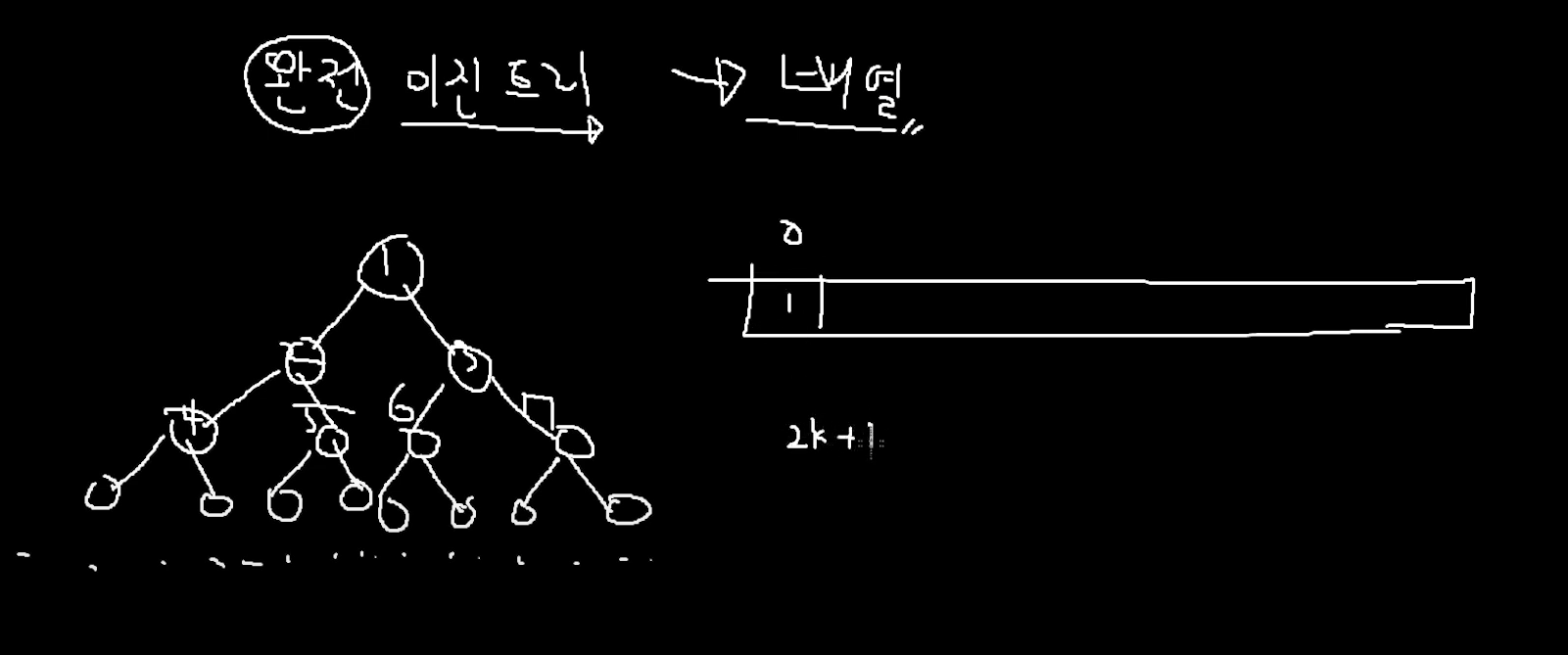
지금 루트 노드의 자식(1번 노드의 자식은)
2k+1이다.
k 에다가 본인의 인덱스 번호(0)을 넣으면 2 * 0 + 1이라 1나온다.
그러면 자식은 1번 인덱스에 있다는 것을 알 수 있다.
그리고 두번째 자식은 2k+2로 접근을 하면 된다.
그러면 2 * 0 + 2 => 2번인덱스 이다.
자식 노드 찾아보기
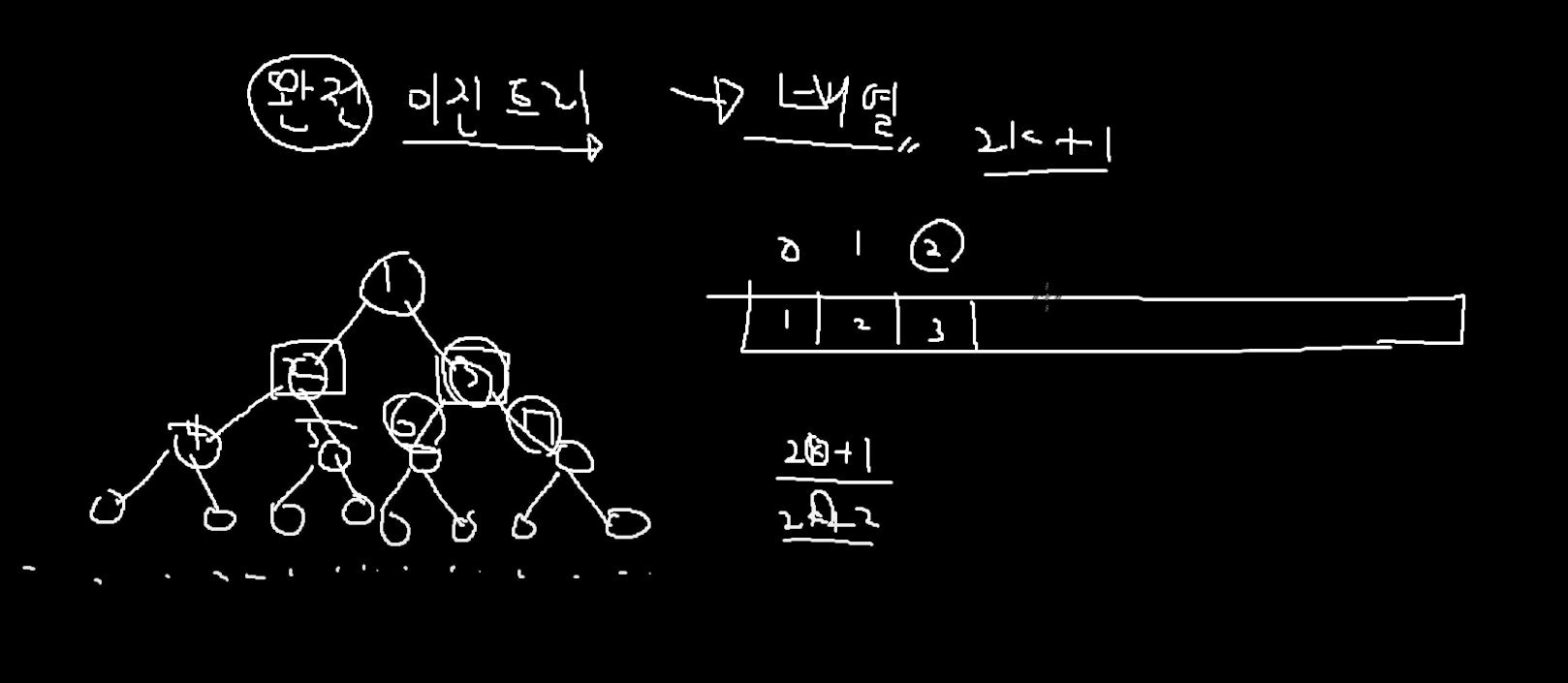
마찬가지로 2번 인덱스 (3번 노드의 자식)을 찾아보려고하면
2k+1
에서 3번 노드의 인덱스는 2이기 때문에
2 * 2 + 1 => 5 번 인덱스를 가르킨다.
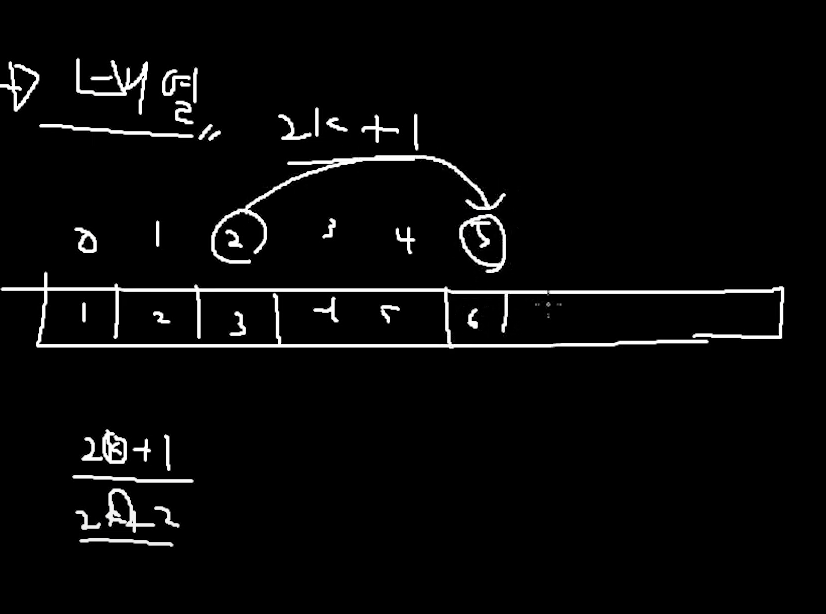
이렇게 6번 노드를 가르킴.
오직 완전 이진 트리에서만 이러한 배열 접근이 가능하다.
자식 -> 부모 추적
2k + 1을 거꾸로 해주면 된다.

자식으 5, 6일 때
5 - 1 = 4, 4에서 / 2 를 하면 => 2번 인덱스 (나머지는 버린다)
이진 탐색 트리
탐색을 위해서 고안된 이진트리.
Binary Search Tree
BST
이진 탐색이란?
예시를 먼저 들면

1~1000번 적힌 카드가 있음
100명이 이 카드를 뽑음. -> 순차적으로 나열을 함.
나는 누가 뭘 뽑았는지 모른다.
그때, 225 번 카드를 뽑은 사람을 찾아야 한다. => "탐색"이다.

최악은 경우는 맨 마지막 사람이 225 들고 있는 경우이다.
100번 탐색을 함.
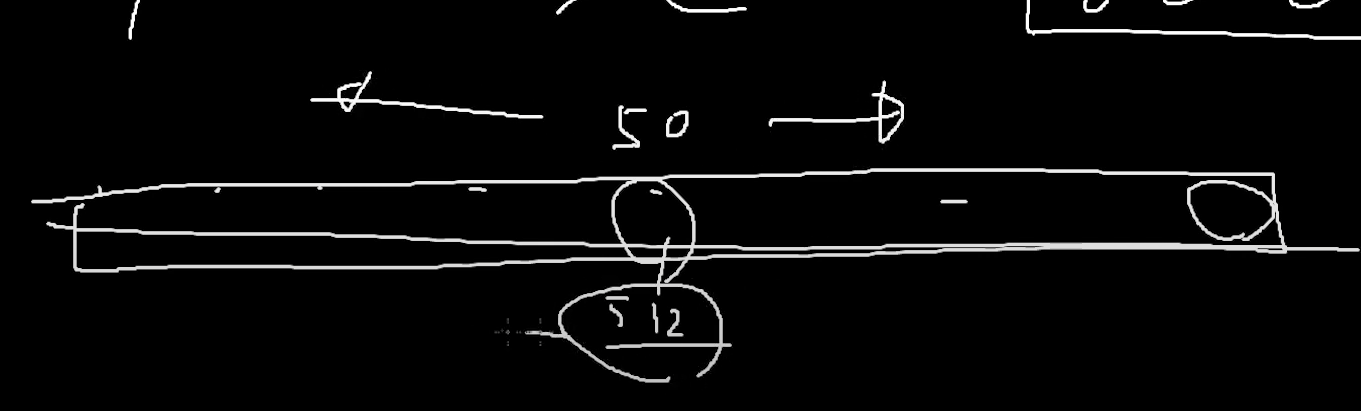
중간에 있는 녀석 인덱스를 뽑아서 번호(값) 확인한다.
그러면 512 가 나왔는데
225는 오른쪽? 왼쪽? => 왼쪽에 있다.
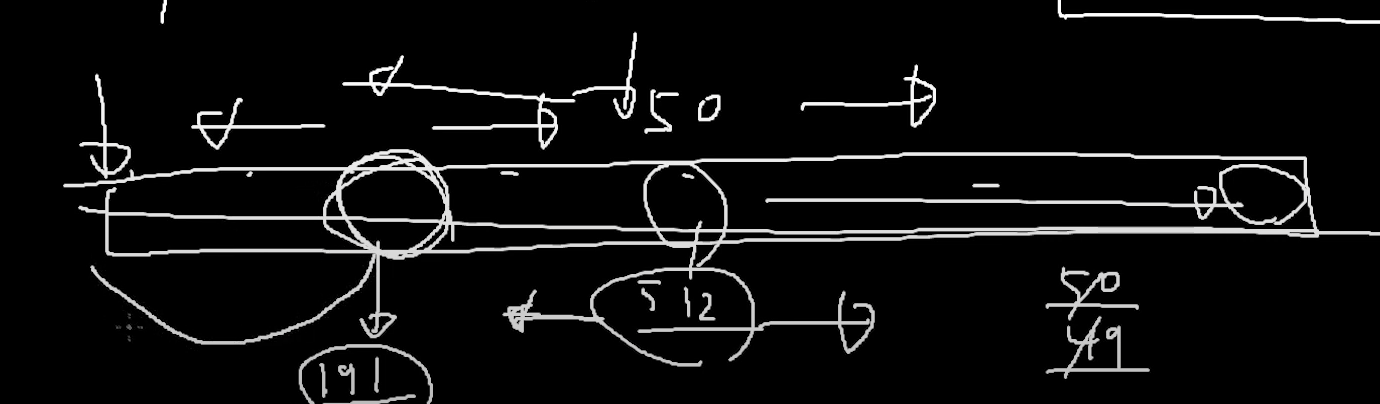
그러면 또 그 중에 녀석을 뽑아서 확인을 한다.
191이라면은 오른쪽으로 간다
[ ][ ] [ ][ ] [ ][ ] [ ][ ] [ ][ ]
[ ][ ] [ ][ ] [ ]
[ ][ ] [
[ ]
약간 이런 느낌으로 반씩 줄어듦.
이진 탐색 조건 ❗❗❗
-
데이터가 정렬되어 있어야함. ❗❗❗ (이게 제일 중요)
-
문제를 절반씩 줄여 나가는 방식.
의 "탐색 방법"이다.
이진 탐색의 시간 복잡도
데이터가 n가 했을 때 최악의 경우의 시간 복잡도는
log2 ^n 이다.
배열이나 리스트의 경우는 O(n)이였음.
로그 계산
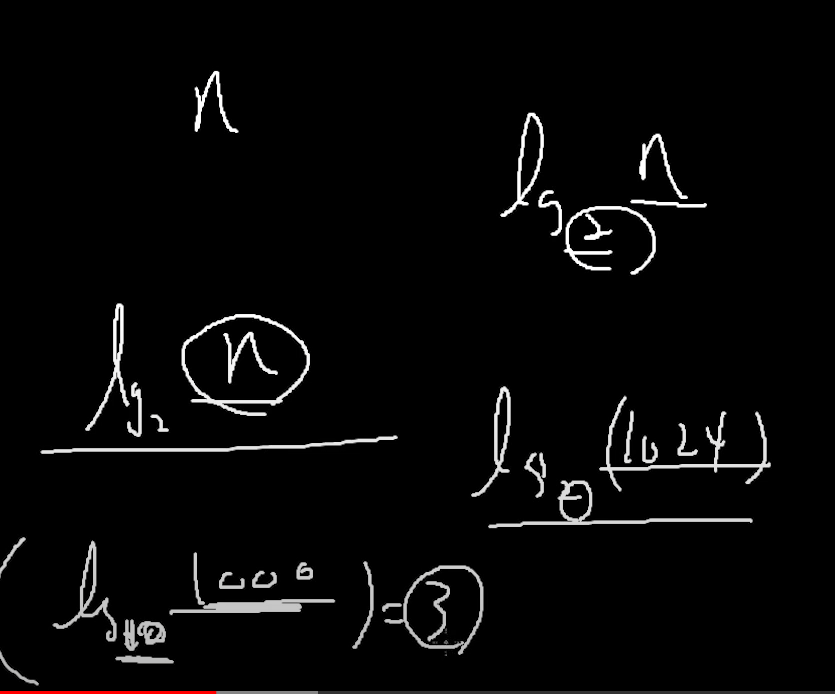
기억나제?
몇승 몇승 이런거.
왜 log2 냐? 🛫🛫🛫

n개의 데이터를 2로 나누고, 또 2로 나누고... 반복임.
쪼개고 쪼개다가 1이 나오는데
그 1에서 2의 몇승을 해야 n이 나오냐? 왜 같은 말이다.

문제를 절반씩 처 나가기 때문에
log2 n 이다.
문제의 크기인 n이 늘어나면 늘어 날 수록 존나 좋다.
로그 성질
log2 n 이 로그의 성질에 의해서
logx n / logx 2으로 분리가 가능함.
logx n의 입장에서는

1 / logx 2 이 "계수"이다.
빅오 표기법에 의해서 계수 무시하면
logx N이 남는다.
그래서 O(logN) 이라고 함.
x는 상관없는 거임.
알고리즘 순위
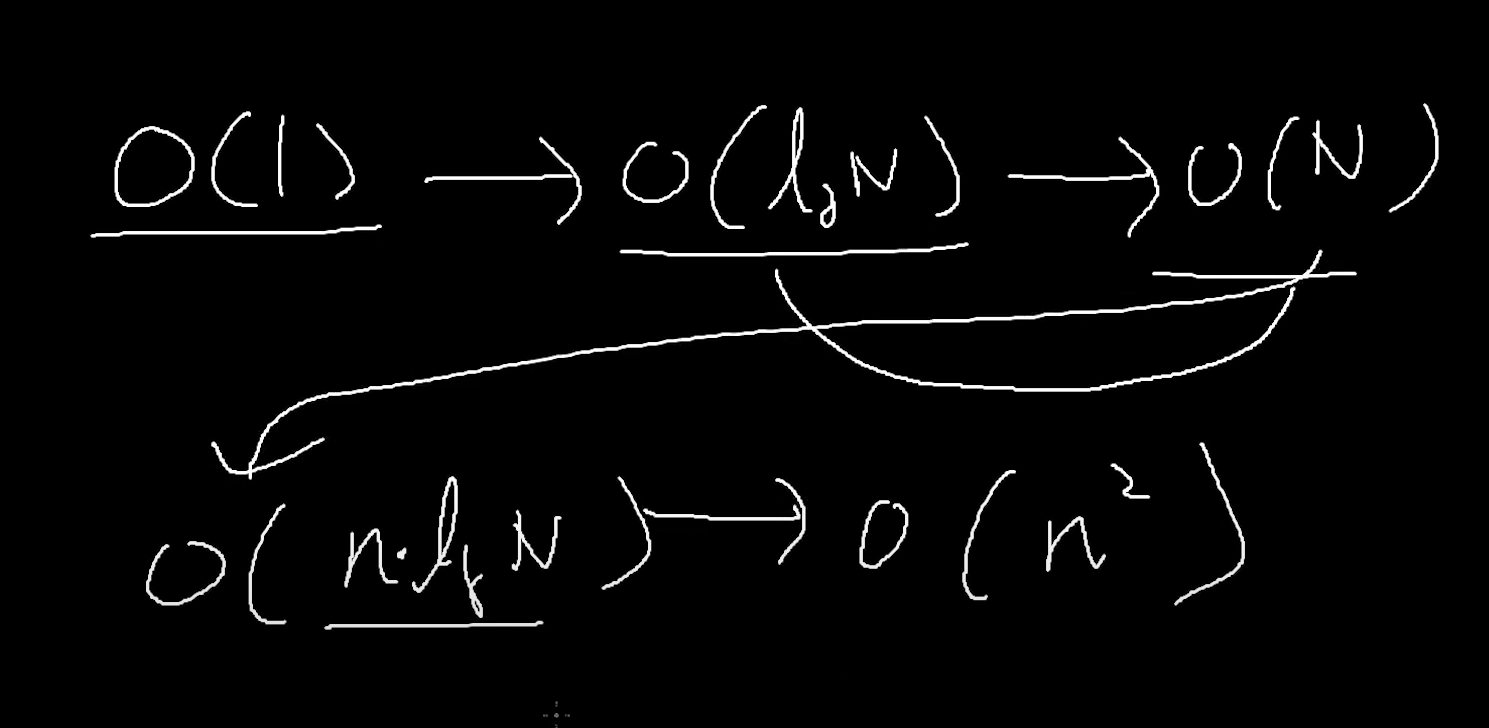
상수가 가장 빠름.
이진 탐색 트리 구현 방법
100을 "루트"라 놔두자.
오름차순으로 정렬을 한다고 하자.
50이라는 데이터 들어고 왔음. 그 이후 300이라는 데이터 들어옴.
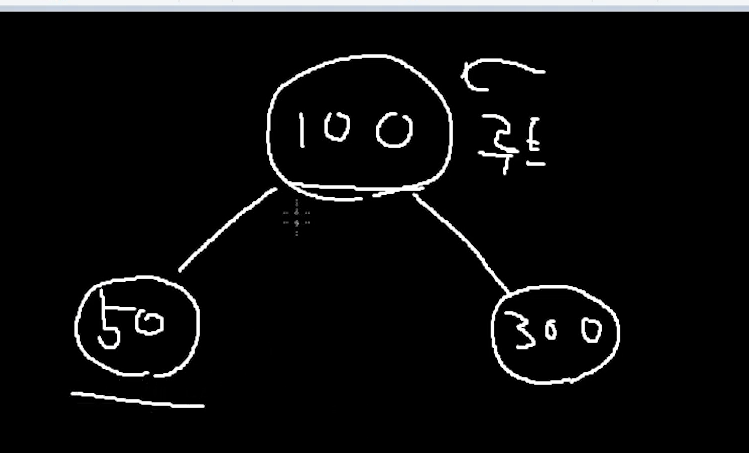
50 -> 100 -> 300 으로 접근을 하면 정렬된 순서이다.
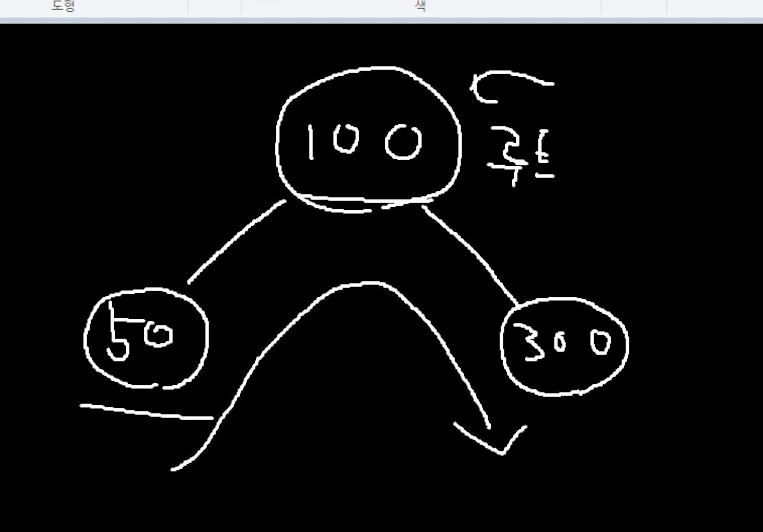
이렇게.
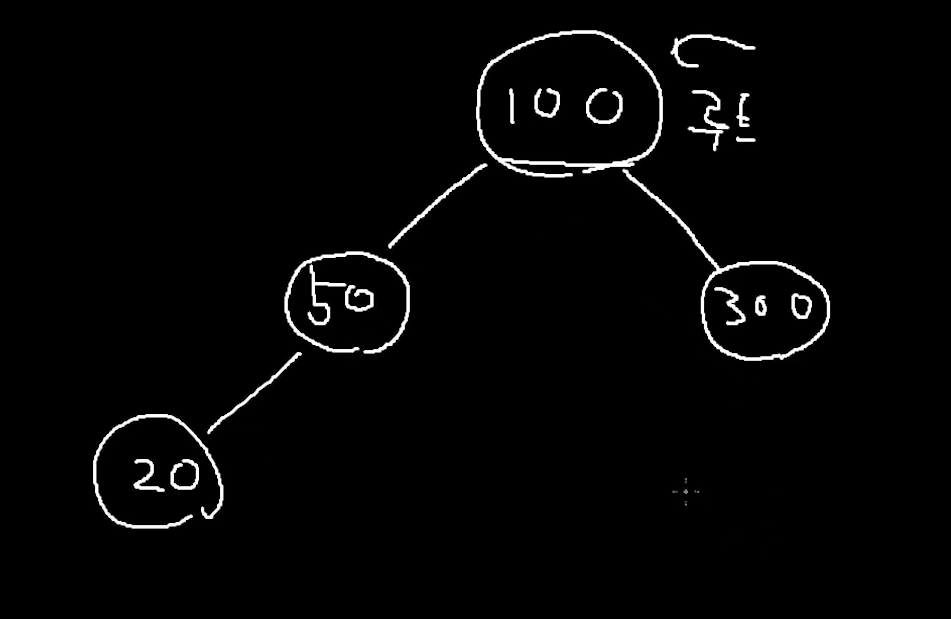
그리고 또 20이라는 데이터 들어갈때
100과 비교를 해서 작은지 큰지를 본다.
작다면 왼쪽, 크다면 오른쪽
그리고 다시 50과 비교를 한다.
그리고 작은지 큰지를 따져서 내려간다. (왼쪽으로)
vector나 list는 탐색을 고려하지 않고 데이터를 넣기 때문에
데이터 넣을때의 시간 복잡도는 O(1) 상수시간이다.
이진 탐색 트리는 "정렬"을 위해서 "손해"를 보고 데이터 넣는다.
"탐색"을 위해서 이런 손해를 감수를 한다.
