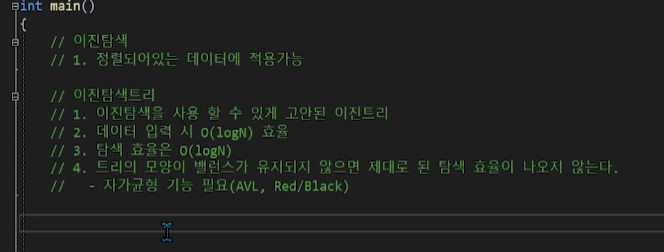
먼저 생각 해야할게
이진 트리
자식이 두개로 제한되는 트리 자료구조
이진 탐색 트리
이진으로 탐색을 하는 트리
완전 이진 트리
자식이 2개씩 꽉 채워 져있는 트리
이진 탐색 트리에서의 "이진 탐색"이란
시간복잡도 O(log N)을 가짐.
반반 씩 나누어서 가다 보니까.
이진 탐색 트리.
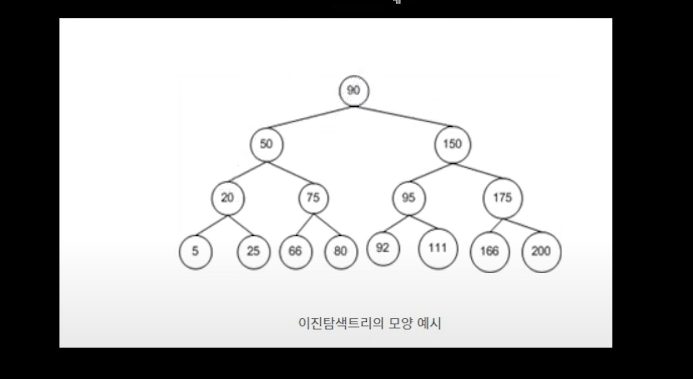
이진 탐색 트리 데이터 추가비용
114를 넣는다고 할 경우
데이터를 집어 넣는 순간부터 비교 횟수가 발생한다.
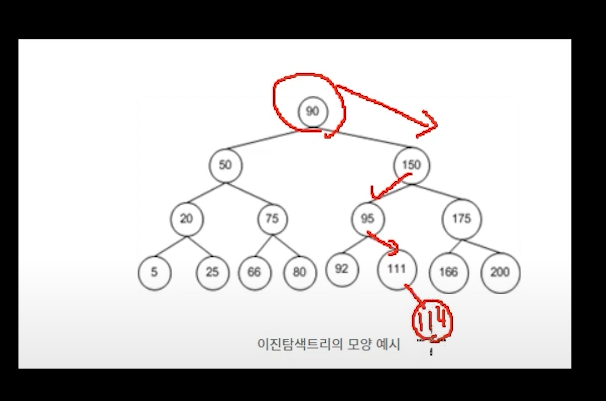
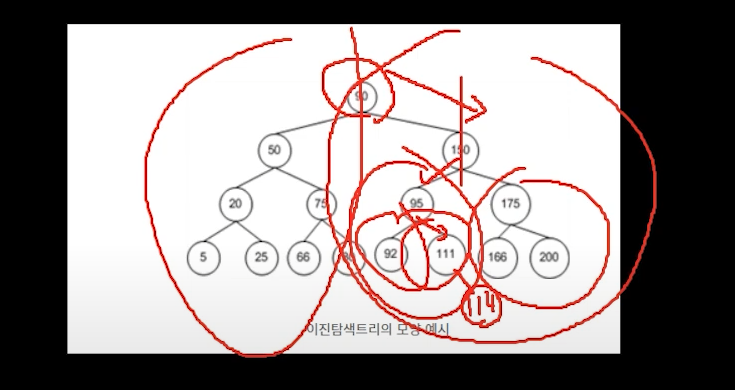
루트와 비교를 하고 나서 데이터 절반으로 줄어들고
그다음 자식인 130과 비교를 하면 데이터가 다시 절반으로 줄어들고...
"탐색"할 때와 비슷(똑같)다.
즉, 데이터를 입력하는 비교 횟수도 logN 이다.
자료구조의 시간복잡도 비교
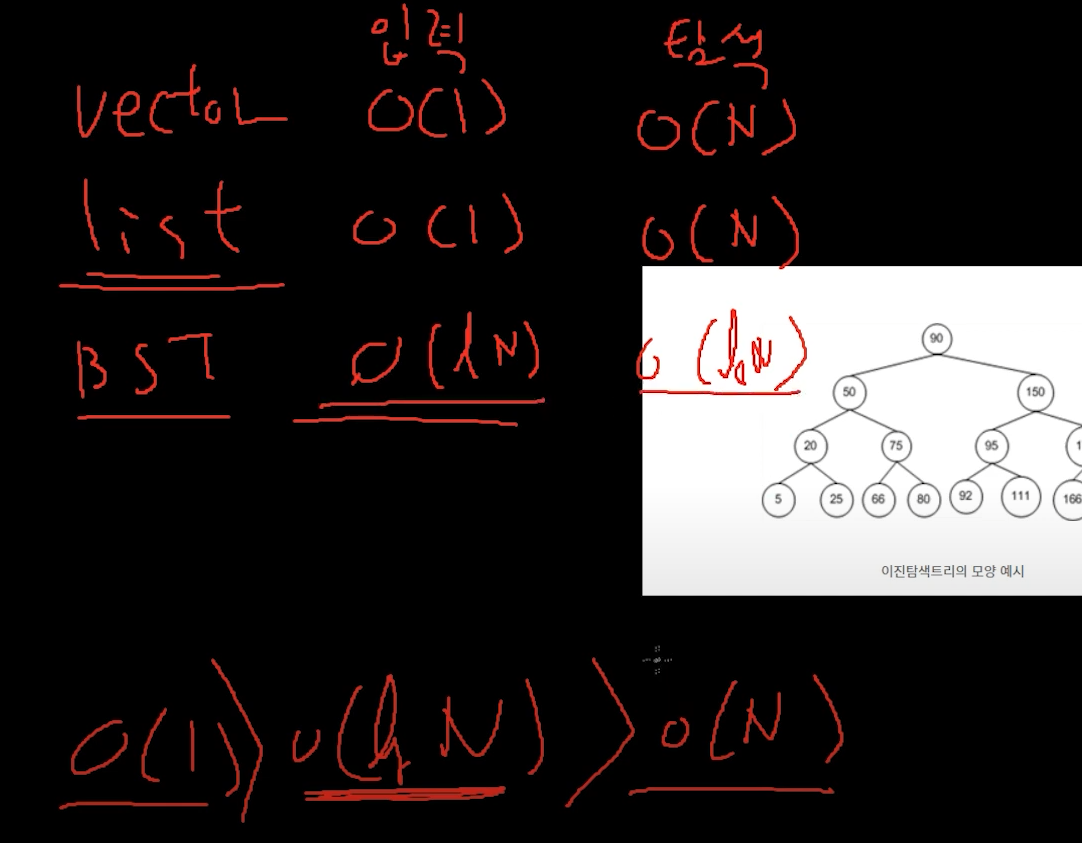
vector, list, 이진 탐색 트리
이런식인데 이진탐색은 입력의 손해를 감수함.
자식 -> 부모 타고 가보기
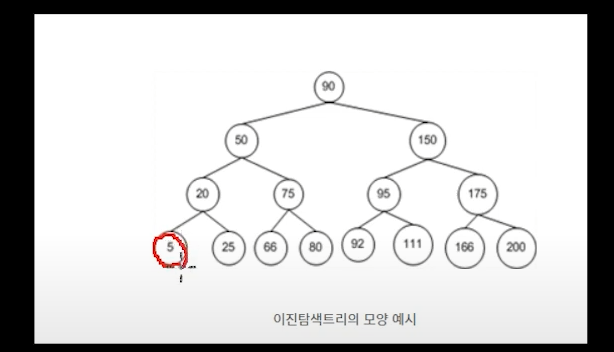
지금 이게 정렬된 구조라고 했는데
자식에서 어떻게 가야 정렬된 형태라고 할 수 있을까?
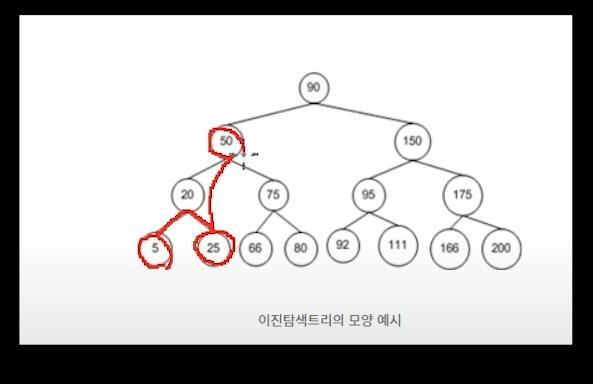
5 -> 20(부) -> 25 -> 50(부모의 부모) -> 75 -> 66 -> 80 -> 90(루트) -> 92(리프) -> 95 -> 111 -> 150 -> 166 -> 175 -> 200
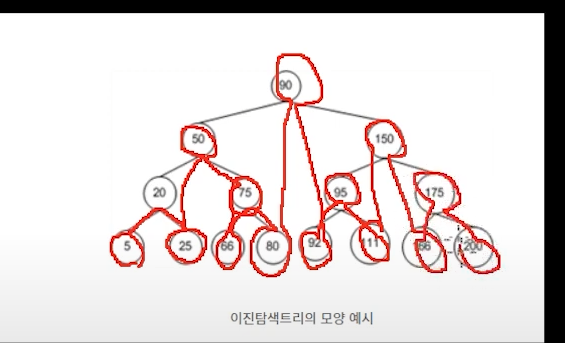
이런식으로 가야됨.
이래야 정렬된 순서로 가는 것임.
중위 순회
트리에서의 이러한 접근 방식을 중위 순회 라고한다.
=> In Order
-
전위 순회 Pre Order
-
후위 순회 Post Order
도 있다.
트리에서 가장 중요한 접근 방법이 In Order이다.
순회의 규칙 ❗❗❗
-
In Order
-
Pre Order
-
Post Order
가 있는데
순회 규칙을 먼저 알아보자.
전위 순회 Pre Order
우선순위가 부모가 제일 높다.
그다음 왼쪽 오른쪽 순서임.
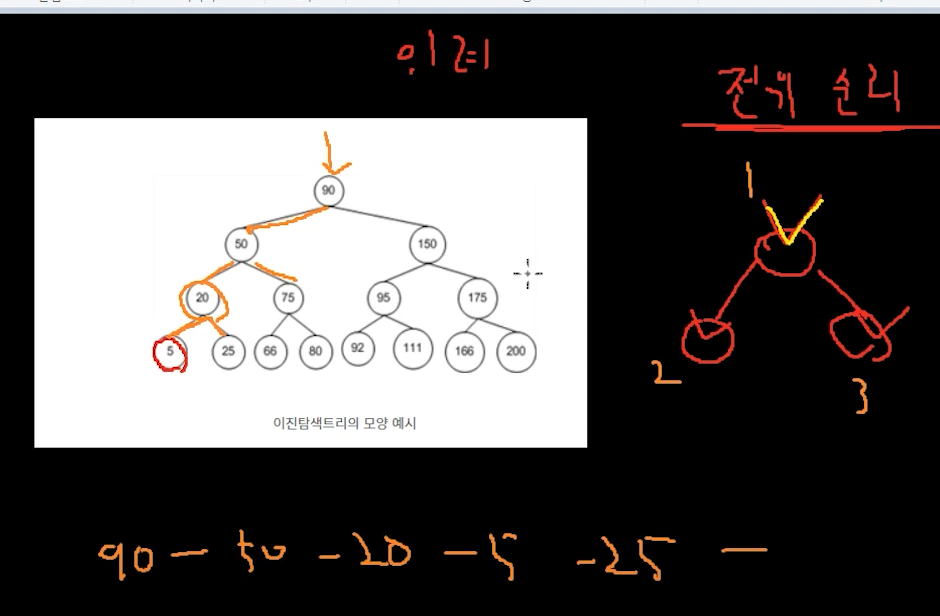
90 -> 50 -> 20 -> 5 -> 25 -> 50 -> 75 -> 66 이런식으로 감.
중위 순회 In Order ❗❗❗
왼쪽 자식이 우선순위가 높다.
그 다음 부모 -> 오른쪽 자식 순이다.
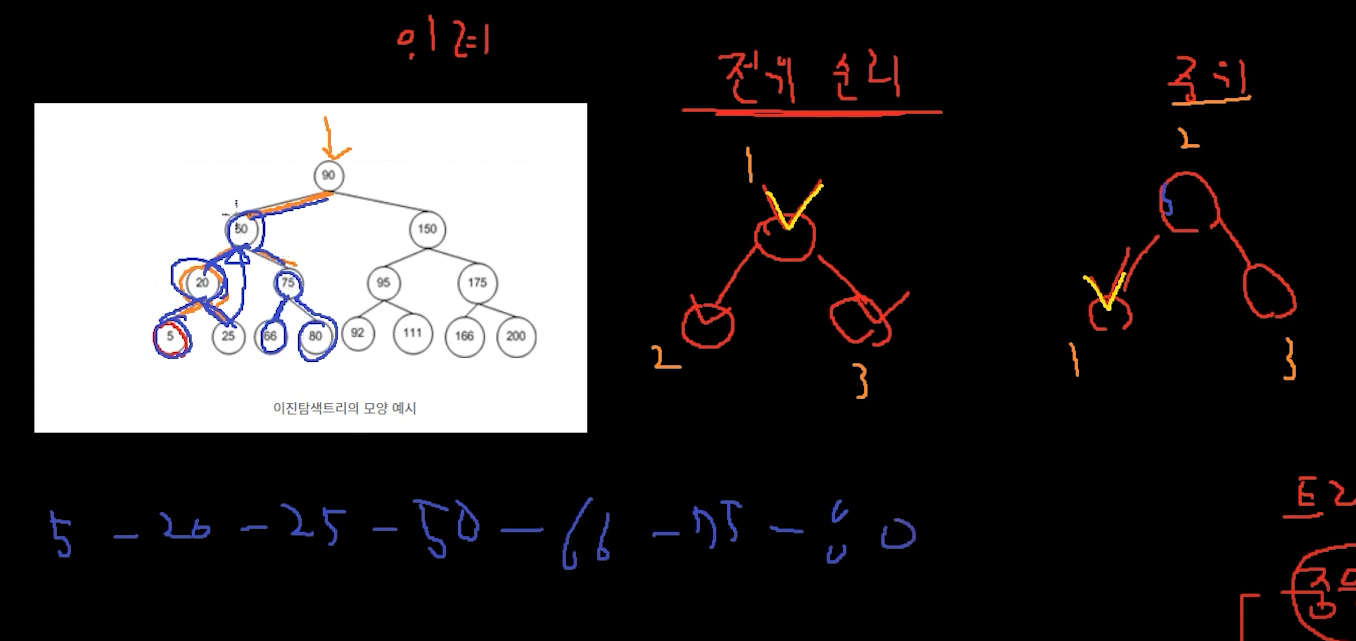
중위 순회로 접근을 하면 이진 탐색 트리에서 정렬된 순서로 접근을 할 수 있다.
후위 순회 Post Order
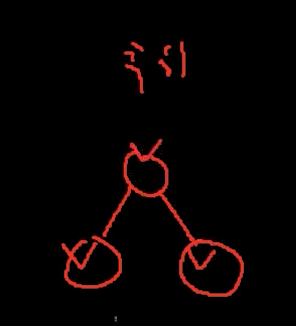
왼쪽 자식, 오른쪽 자식이 순위가 높고
부모가 마지막이다.
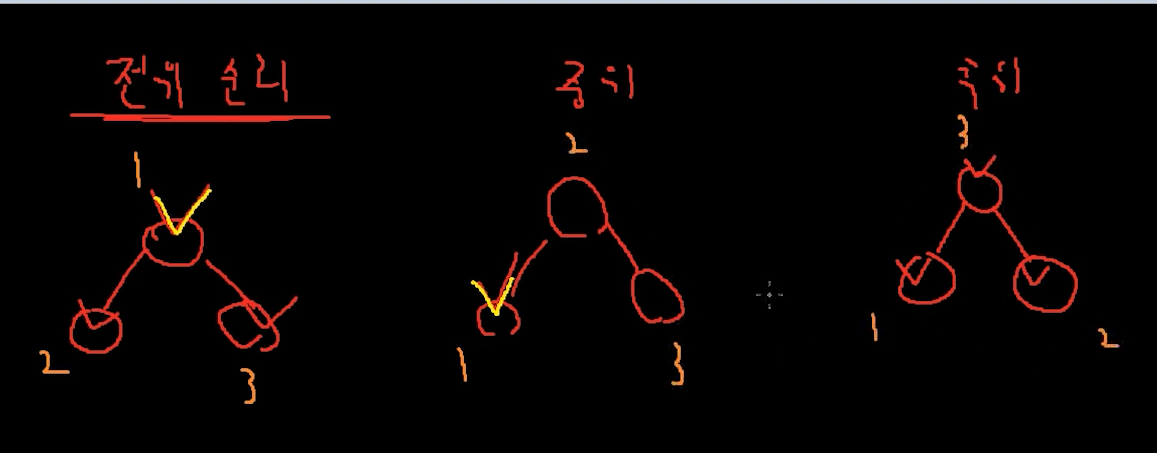
순서를 적으면 이런식이다.
중위 순회를 기준으로
이전 노드 다음 노드
-
중위 후속자
-
중위 선행자
ㅇㅣ것들은 중위 순회를 기준으로 다음 노드(중위 후속자)와 이전 노드(중위 선행자)를 가르킴.
iterator이다.
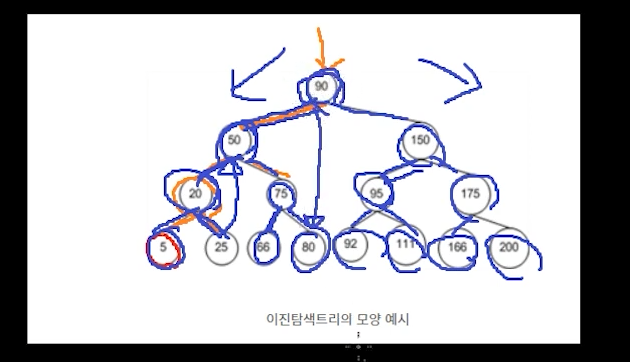
90이라는 루트 노드 기준으로 중위 선행자가 바로 80이라는 노드이다.
90이라는 루트노드의 중위 후속자는 92 이다.
이진 탐색 트리의 문제점
데이터 입력이 순차적으로 진행될 경우

1~1000 넣을 경우 이렇게 될듯.
계속 오른쪽으로 들어감.
1000을 찾으려고하면은 1000번 찾음...
가장 황밸은 데이터 들의 값들 중에 가장 가운데가 좋은데...
이게 항상 어떻게 그렇게 보장을 하노?
그럴 수는 없다.
따라서 실제 프로그래밍 상에서 구현을 할 때,
이진 탐색 트리의 탐색 알고리즘만으로만 탐색을 하지 않는다.
그래서
"self balanced" 자가 균형 이진 탐색트리 == BST 를 추가를 해서 사용한다.
self balaced
self balaced 의 기능을 가지는 BST(이진 탐색 트리)가 있는데 이것의 대표적인 예로
-
AVL tree
-
Red Black tree
이렇게 있다.
Base는 이진 탐색 트리인데 "자가 균형 기능"이 구현이 되어있는 애들이다.
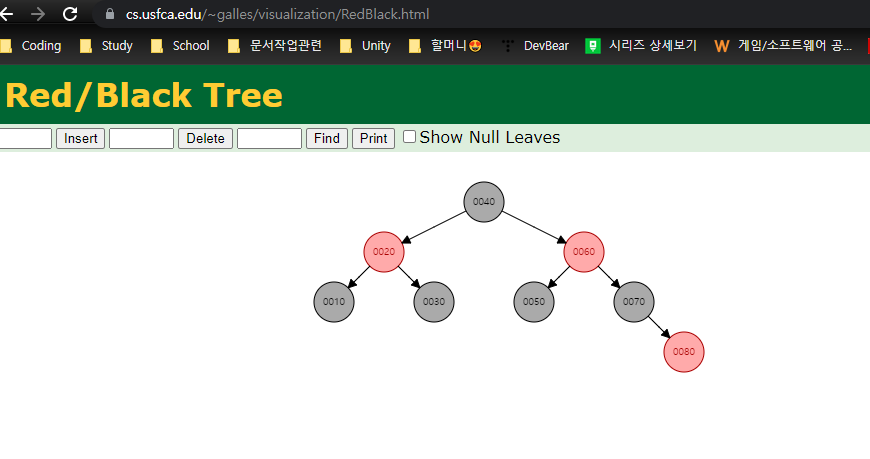
순차적으로 넣는 최악의 경우를 방지하기 위해서
self balanced를 사용한다.
이것을 사용한 이진 탐색 트리의 대표적인 예로
AVL, Red Black이진 탐색 트리가 있다.
이진 탐색을 사용할 수 있게 만든 트리가
이진 탐색 트리 이다.
"트리"랑은 무관.
데이터를 절반씩 줄여가면서 원하는 데이터를 찾는 방식을 이진 탐색이라고 한다.
트리에만 적용되는 개념이 아니다.