힙 트리 이론

priority_queue를 지탱하는 이론이다.

힙 트리도 트리라서 일단 이진트리부터 보도록 하자

1. 이진 검색 트리

각 노드가 최대 두개의 자식 노드를 가지는 트리

없을 수도 있고 하나만 있을 수도 있음.

그러면 이진트리 왜 사용하나?

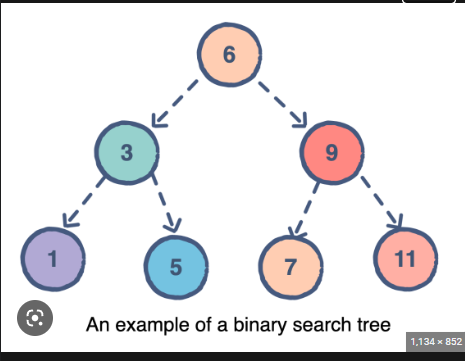
binary search(이진 검색)를 사용할려고 이진 검색 트리를 사용한다.

2. 이진 검색 트리 문제점

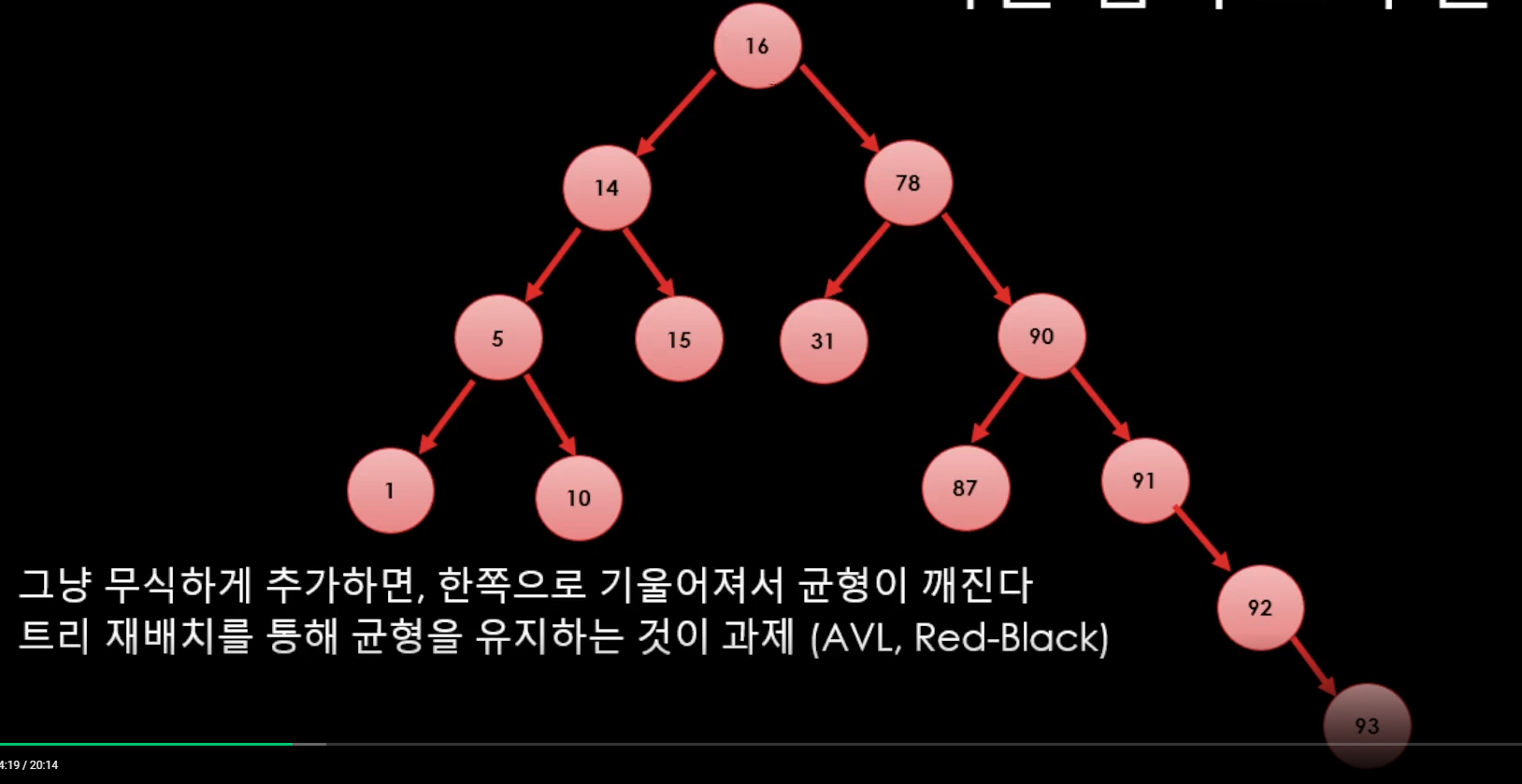
이런경우 문제가 생기는데

나중에 이진 검색트리를 구현을 할 때 특정 알고리즘을 적용해서 트리를 재배치를 해서 균형을 유지할 수 있도록 해야한다.

(나중에 따로 연습을 한다)

3. 힙 트리👍

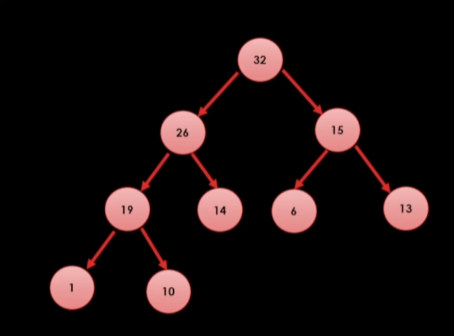
공식적인 법칙은 아닌데 일단 R이 만든 법칙이 있다.

• 힙 트리 1법칙 : [부모 노드]가 가진 값은 항상 [자식 노드]가 가진 값보다 크다.

  그래서 이진 검색 트리보다는 간단하다. 무조건 부모가 자식보다 크기만 하면 되니까

  ❗ 마지막 Level을 제외한 모든 레벨에 노드가 꽉차 있어야한다(완전 이진 트리)

  ❗ 마지막 Level에 Node가 있을 때는, 항상 왼쪽부터 순서대로 채워야 한다.

• 힙 트리 2법칙 : 노드 개수를 알면, 트리 구조는 무조건 확정할 수 있다.

이 힙 트리 2법칙으로 인해서 -> 트리 구조가 확정이 된다는 특징에 의해서

편한 특징을 하나 얻을 수 있는데,

"배열"을 이용해서 힙 구조를 바로 표현할 수 있다.

정수 / 정수 ❗

3번 규칙에서 4번 노드의 경우 부모를 찾을려면

(4 - 1) / 2 번이 4번의 부모노드인데

3 / 2이다. 1.5인데

C++, C# 특성상 정수 자체가 소수점을 날려서 계산을 하기 때문에 1나옴.

4. Value Insert

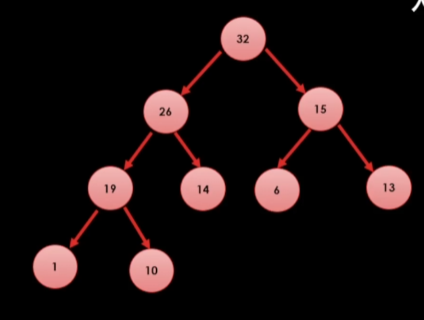
현재 이 상태에서 31이라는 값을 넣을려면?

먼저 힙 트리 2법칙을 지켜준다.

=> 구조를 맞춰 준다. (마지막 Level을 제외하고는 완전 이진 트리이여야 한다)

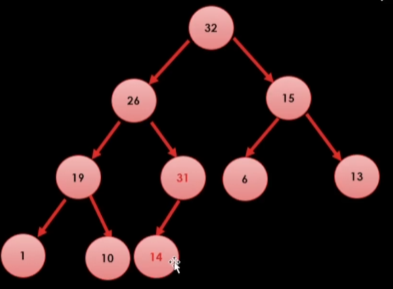
힙 트리 1법칙을 만족하기 위해 도장깨기 하러간다.

부모가 항상 자식보다는 커야 하니까!

5. Get Max Value

최대값 꺼낼 경우

최상위에 있는 root node만 꺼내면 된다.

힙트리 쓰는 이융가 전체 데이터를 관리를 할 때 사용하는게 아니라 최대/최소 값만을 빠르게 찾을 때 좋은 자료구조임.

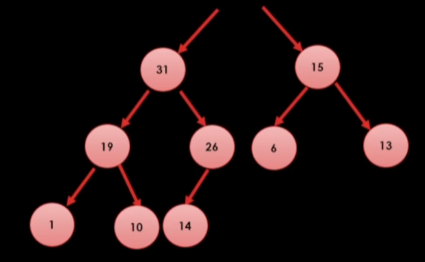
먼저, 이렇게 대가리를 자른다.

그리고 value insertion을 할 때와 마찬가지로

힙 트리 2법칙부터 챙겨주도록 하자.

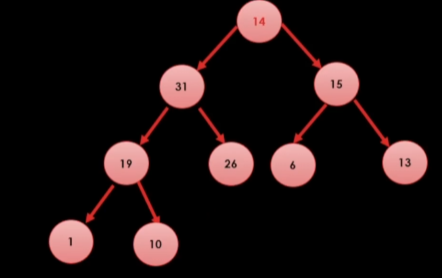
그래서 튀어나가 있는 14를 제일 위로 보낸다.

이후 힙 트리 1법칙을 지켜주면은 된다.

31, 15 둘중에 더큰 값과 도장 깨기를 할 것이다.

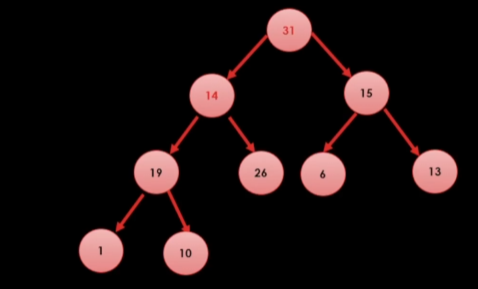
이렇게 내려보내고 마찬가지로

14의 자식인 19, 26중에 큰 26과 도장깨기를 하러간다.

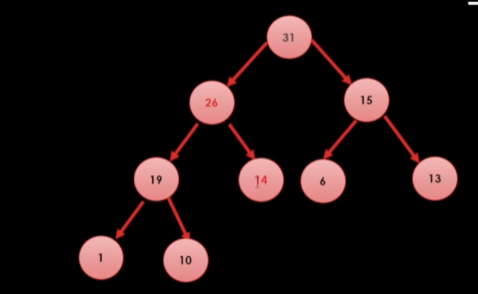
이렇게 변경을 해주면된다.

6. 적용 시킬 부분

Dijkstra에서 가장 좋은 후보군을 찾을 때,

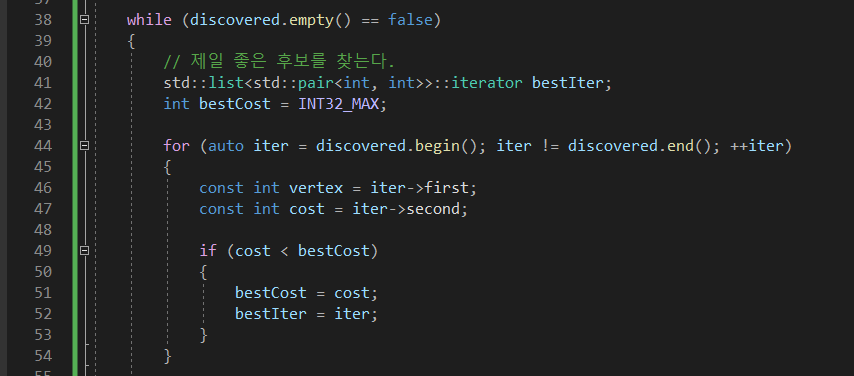
여기서 list를 쭉 다 순회를 해서 찾았는데

데이터가 1000만개 면? 말이 안됨.

이부분을 오늘 배운 힙트리로 대체를 할 거임.
우선순위 큐나.

---

queue에서 데이터를 밀어 넣을 때 밀어 넣은 순서대로 뽑는게 아니라

원하는 최대/최소 조건을 먼저 추출 하는게

우선순위 큐이다.

이 우선 순위 큐가 힙 트리 구조로 구현되어있는것이다.