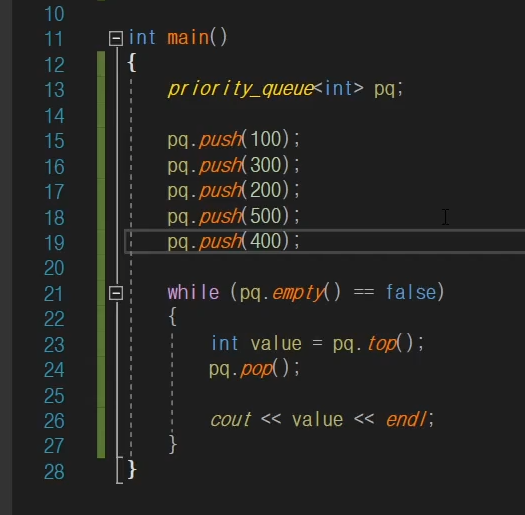
기본적인 queue와 사용 방법은 거의 똑같은데

다른점은 내림차순으로 결과값이 나온다는 것이다.

그런데 작은 값부터 나오게 하고싶다면은 애초에 push할때 음수값을 넣어도 되지만 (너무 야매이다)

2번째, 3번째 인자에 container와 pr을 정해줄 수 있다.

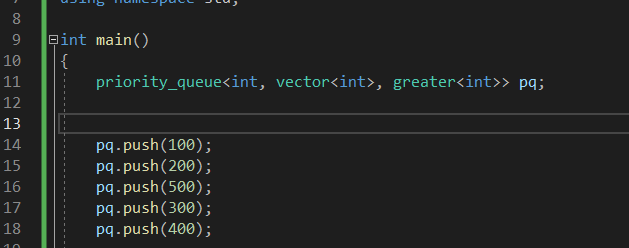
이렇게 greater < int >로 해주게되면 작은 값부터 나오게 된다.

구현하기

• std::swap : 객체도 바꿔줌. 객체안의 데이터도 swap해주고.

  

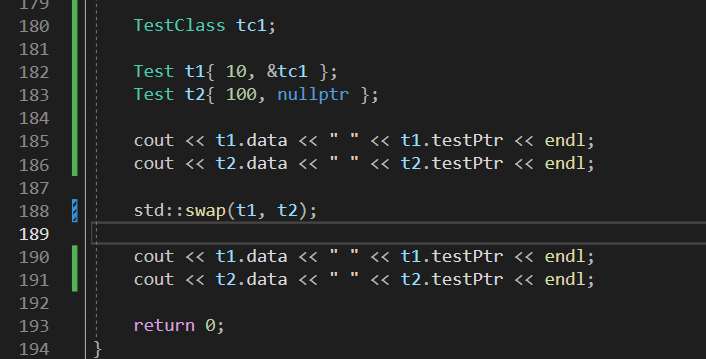
트리 구조로 힙트리가 구현되어 있기 때문에

굳이 노드를 사용하지 않고 배열을 이용해서 구현이 가능하다.

template <typename T, typename Container = std::vector<T>, typename Predicate = less<T>>
class PriorityQueue
{
public:
	void push(const T& data)
	{
		// 힙구조 맞추기
		_heap.push_back(data);
		
		// 도장깨기
		int now = static_cast<int>(_heap.size()) - 1;

		while (now > 0)
		{
			// 현재 (index - 1) / 2 => 부모 인덱스
			int next = (now - 1) / 2;
			
			// 부모 노드와 비교해서 더 작으면 패배
			if (_predicate(_heap[now], _heap[next]))
				break;

			// 데이터 교체
			std::swap(_heap[now], _heap[next]);
			now = next;
		}
	}

	void pop()
	{
		_heap[0] = _heap.back();
		_heap.pop_back();

		int now = 0;

		while (true)
		{
			int left = 2 * now + 1;	 // left = 2 * i + 1
			int right = 2 * now + 2; // right = 2 * i + 2

			// leaf에 도달한 경우
			if (left >= (int)_heap.size())
				break;

			int next = now;

			if (_predicate(_heap[next], _heap[left]))
				next = left;

			if (right < (int)_heap.size() && _predicate(_heap[next], _heap[right]))
				next = right;

			if (next == now)
				break;

			std::swap(_heap[now], _heap[next]);
			now = next;
		}
	}

	T& top()
	{
		return _heap[0];
	}

	bool empty()
	{
		return _heap.empty();
	}

private:
	Container _heap = {};
	Predicate _predicate = {};
};

1. Predicate ❗

• Predicate

  http://egloos.zum.com/sweeper/v/2819496

  bool을 반환하는 함수객체이다.

Predicate가 less면은 우선순위 큐에서 큰 값부터 나오고

greater라면은 가장 작은 값부터 튀어나온다.

less, greater, plus, minus가 있는데

STL에서 유용하게 사용하는 "함수 객체"이다.

• 함수 객체

  https://xzio.tistory.com/272

• 함수 객체란?

  https://blog.hexabrain.net/267

  함수 객체에 정수형 데이터를 넘겨주면 그 값을 받아 누적시키고 반환하게 되며, 동작을 포현할 수 있으나 상태를 저장할 수 없는 일반 함수와는 상당히 비교가 되죠? 함수 객체를 사용하면 일반 함수보다 더 폭넓게, 유연하게 사용할 수 있습니다.

2. 이해 안 갔던 부분 ❗

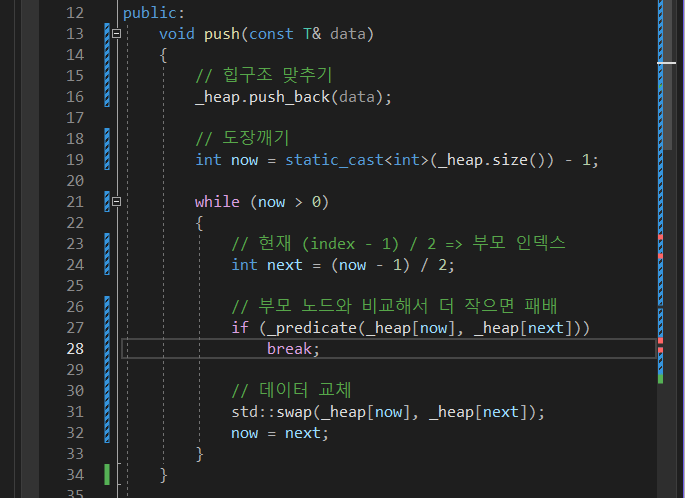
지금 push하는 부분에서 27번째 줄에서

_predicate(_heap[now], _heap[next])
	break;

이 부분인데

_predicate가 지금

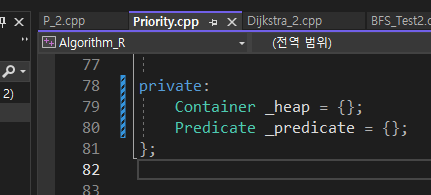
PriorityQueue의 멤버 변수이다. 객체를 만들어줌.

기본값으로 less< T > 를함.

less일 경우 첫번째 인자가 두번째 인자보다 작으면 true,

greater일 일경우 첫번째 인자가 두번째 인자보다 크다면 true반환.

그래서

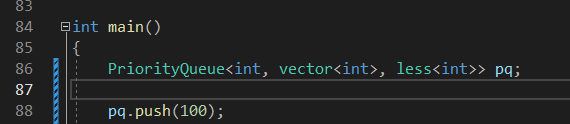
우선순위 큐 만들때 less로 해주게되면은

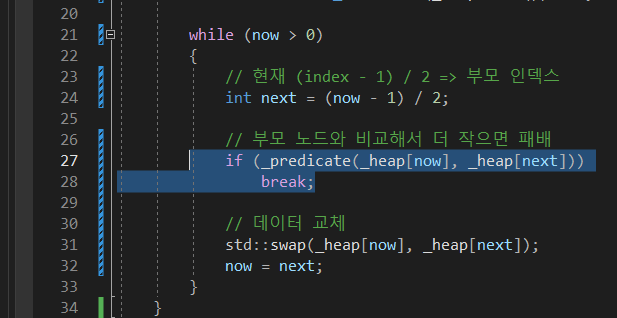
이부분에서 100이 root 이고 새로 넣은 데이터가 200이라 가정을 하면은

100이 더 작기 때문에 true를 반환해서 break만남.

31번째 줄까지 내려와서 swap하는 일이 없음.. 그래서 less일 경우 가장 작은 수부터 나오게됨.

정리 👍

힙 트리 구조를 유지를 해야하고,
1법칙, 2법칙 지키기만 하면된다.
그리고 push하는 경우 O(log n)을 가짐.
pop을 할 때에도 O(log n)을 가짐.
절반씩 떨어져 나가기 때문에.

힙트리 2법칙으로 인해 노드의 갯수를 알면은 트리 구조가 확정이라

struct Node {} 이런거 안 만들고 배열로 관리가 가능함.

그래서 index = 3일 때,
index의 왼쪽자식 : 2 index + 1
index의 오른쪽 자식 : 2 index + 2,
index의 부모 : (index - 1) / 2