
Quick Select란?
정렬되지 않은 Array에서 N번째로 큰 || 작은 element를 찾는 방법이다.
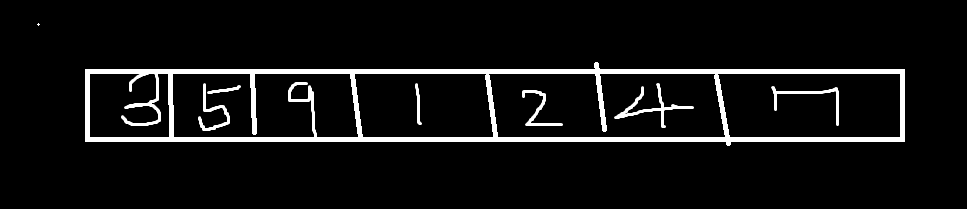
에서 2번째로 큰 수를 찾을 경우.
방법
1. Heap정렬 => 진행
Heap정렬을 한 뒤, 뒤에서 두번째 원소 뽑아내면된다.
이럴경우 시간 복잡도는 해당 Array를 정렬하는데 필요한 시간 O (N log N)인데
힙정렬 후에 뒤에서 두번째 꺼내면됨.
근데 이거보다 더 빠르게 동작하게 만들어라고 하면
"Partition"을 사용해야한다.
2. Partition
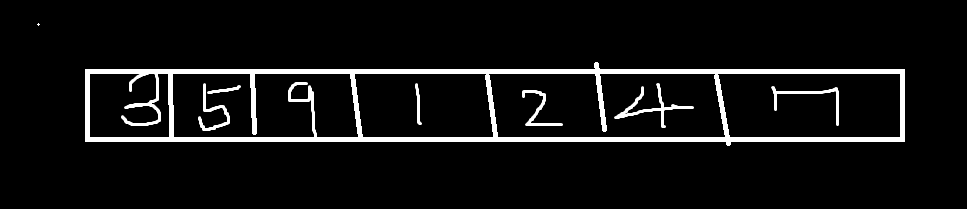
여기서 기준을 잡는다. (아무거나 잡아도 상관없음)
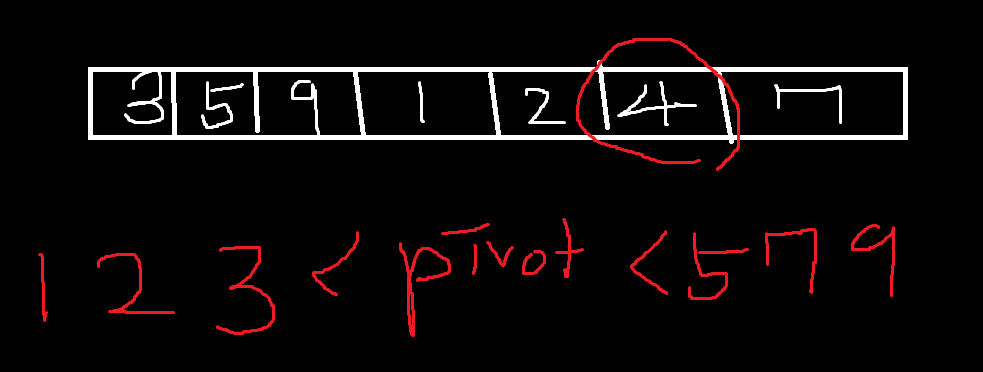
이렇게 잡음.
과정
1단계
pivot으로 잡은 수와 가장 끝 수를 swap해준다.

pivot number는 4인 상태에서 왼쪽끝과 오른쪽끝에 pointer를 잡아준다(pivot을 잡아준다)
노란색 pointer는 pivot보다 작은수를 왼쪽에 두고
초록색 pointer는 pivot보다 큰 수를 오른쪽에 두개 만들면 된다.
노란색 pointer보다 작으면 ++로 이동시킨다.
데이터를 확인후 pivot보다 크다면 멈춘다.
초록색 point데이터를 확인후 pivot과 비교를 한다. 크다면 --로 왼쪽으로 이동시킨다.
그러다 pivot보다 작다면 멈춘다.
2단계

여기에서 이제 진행을 할 수 없기 때문에
노란색과 초록색을 swap해준다.

이후 1단계를 다시 반복을 한다.

여기서 다시 멈춘다.
멈추었다면 두 데이터를 swap해준다.
3단계

두수를 swap을 한뒤 다시 1~2단계를 진행을한다.
1은 pivot(4)보다 작기 때문에 ++로 ->로 이동
9는 pivot보다 크기 때문에 --로 <- 이동

두 pointer가 역전이 발생을 함.
역전이 발생한 기준으로 보면은 노란색 pointer 왼쪽에는 pivot보다 작은 값들이,
초록색 pointer보다 오른쪽에는 pivot보다 큰 데이터들이 몰린다.
노란색 pointer가 가르키는 데이터와 pivot데이터를 swap해준다.

그러면 이런 Array가 만들어 진다.
이렇게하면은
최초에 pivot으로 잡았던 데이터보다 작은 부분들은 왼쪽에 다 몰리고 큰부분은 오른족에 몰리게 된다.
하지만 아직 2번째로 큰 수는 뭔지는 모른다.
다만 4보다 큰 수가 몰려있는 부분에서 Quick Select를 한번만 진행해주고 두번째로 큰수를 찾으면 전체 Array에서 두번째로 큰 수를 찾게된다.
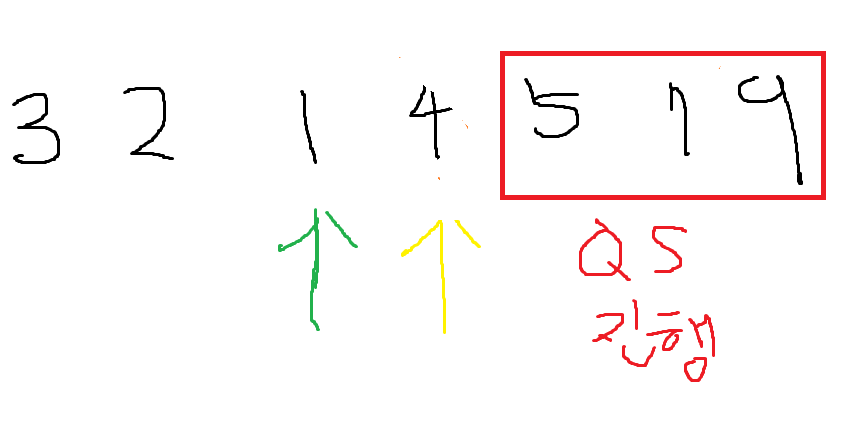
그럼 다시 Quick Select를 진행을 하면은
pivot을 7로 잡고 마지막 데이터와 교환을 한다.


마찬가지로 pointer를 잡고 노란색 왼쪽에는 pivot보다 작은 데이터를
초록색 pointer는 pivot보다 큰 데이터를 오도록 만든다.
5는 7보다 작기 때문에 ++로 ->이동을 한다.
9는 7보다 크기 때문에 -- <- 이동을 한다.

역전이 발생했기 때문에
노란색 pointer와 pivot을 swap한다.
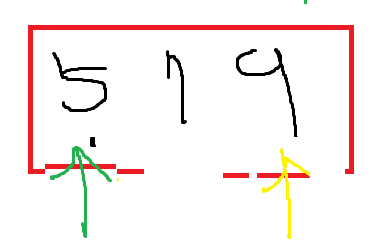
이렇게 되면은 7이 전체 Array에서 두번째로 큰 수라는 것을 알 수 있다.
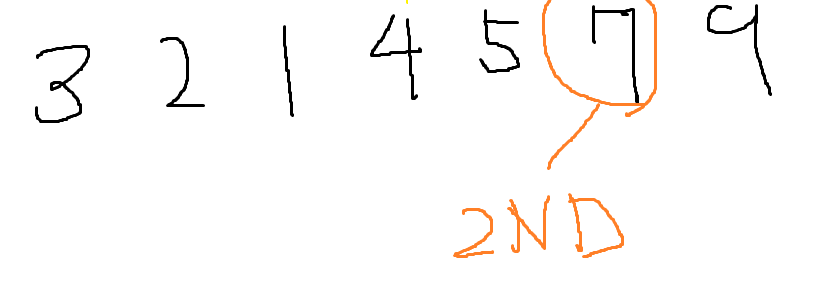
Quick Select 시간 복잡도
-
Worst
pivit을 잡는 과정에서 최악으로 계속 잡을 경우,
Array데이터 갯수 = N,
Pivot을 잡는 횟수 = N
이 두개가 곱해져서 O(N^2)이 된다. -
Best
최고는 바로 만약 N번째로 큰수를 찾고 싶다고 할 경우 전체 Array에서 N번째로 큰 수를 잡는 경우
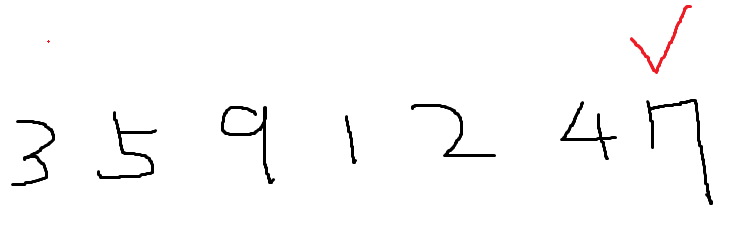
바로 pivot을 7로 잡는 경우 => O(N)이다.
- Avg
결론은 O(N)이기는 한데 이것을 증명하려면 "수학적 증명"이 필요하기 때문에 증명은 안할껀데
간단하게 보자면은,
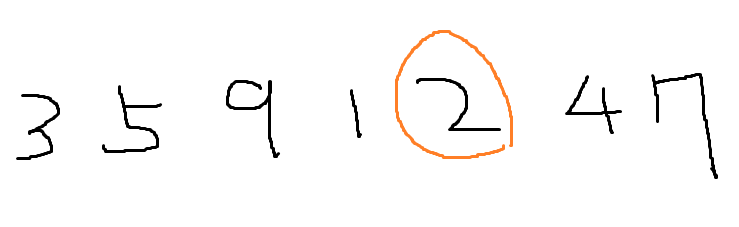
먼저 pivot을 잡고 재귀적은 partition을 진행을 하기때문에 O(N)을 가진다.
Pivot을 무엇을 잡느냐에 따라서 다르다.
python 코드
from typing import List
import random
#return kth largest number
def quickSelect(nums:List[int],k:int) -> int:
length = len(nums)
if length == 1:
return nums[0]
pivotIdx = random.randrange(length)
lastIdx = length-1
nums[pivotIdx],nums[lastIdx] = nums[lastIdx],nums[pivotIdx]
leftIdx = 0
rightIdx = length-2
pivot = nums[-1]
while leftIdx <= rightIdx:
if nums[leftIdx] <= pivot:
leftIdx += 1
continue
if pivot < nums[rightIdx]:
rightIdx -= 1
continue
if pivot < nums[leftIdx] and nums[rightIdx] <= pivot:
nums[leftIdx], nums[rightIdx] = nums[rightIdx], nums[leftIdx]
continue
nums[leftIdx],nums[lastIdx] = nums[lastIdx],nums[leftIdx]
if leftIdx == length - k:
return nums[leftIdx]
elif leftIdx < length-k:
#list slicing creates copy.
return quickSelect(nums=nums[leftIdx+1:],k=k)
elif length-k < leftIdx:
#list slicing creates copy.
return quickSelect(nums=nums[:leftIdx],k=k-(length-leftIdx))
quickSelect(nums=[5,7,9,3,1,2,4],k=2)