1. Heap Sort

기존의 PQ를 직접 구현을 해서 사용을 할 수도 있지만 일단 std::pq를 사용해서 구현을 하면 이렇게 된다.

그리고 우선순위큐의 push의 시간 복잡도는 O(lon n)인데 데이터가 n개니까 O(n log n)이된다.

버블, 선택, 삽입 보다는 훨씬 낫고 사용할 만한 정도이다.

2. 병합 정렬

https://dpdpwl.tistory.com/53

내가 글로적는거보다 이론이 잘 정리 되어있는거 같다.

"분할 정복"이라는 개념이 들어간다.

"Divide And Conquer"

먼저 분할을 한다음에,

각 부분에서 정렬을 하면은

A = [2][3][7][K], B = [4][8][9][J]

이상태에서 A[0], B[0]를 비교를 해서

[2]를 놓는 식으로 제일 앞에 오는 수들끼리 비교를 한다 (정렬이 되어잇으니까)

이거는 큰 그림이고 재귀적으로 타고 갈 수 있다.

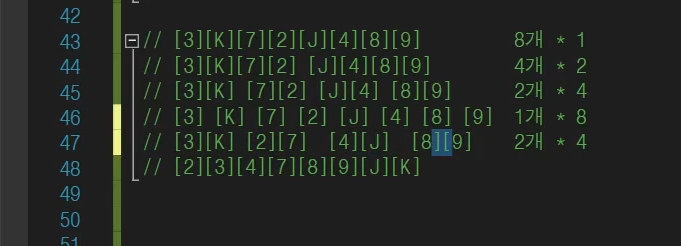
1개까지로 분할을 한 뒤, 2개씩으로 정렬하여 합칠 수 있다.

어렵거나 양이 많은 부분을 분할하여 일처리를 맡긴다는 컨셉이 유용한 경우가 많다.

나중에 멀티 쓰레드 환경같은데서도 다른쓰레드한테 일을 맡긴다거나 그럴 경우에도 고려해 볼 수 있다.

병합 정렬 시간복잡도

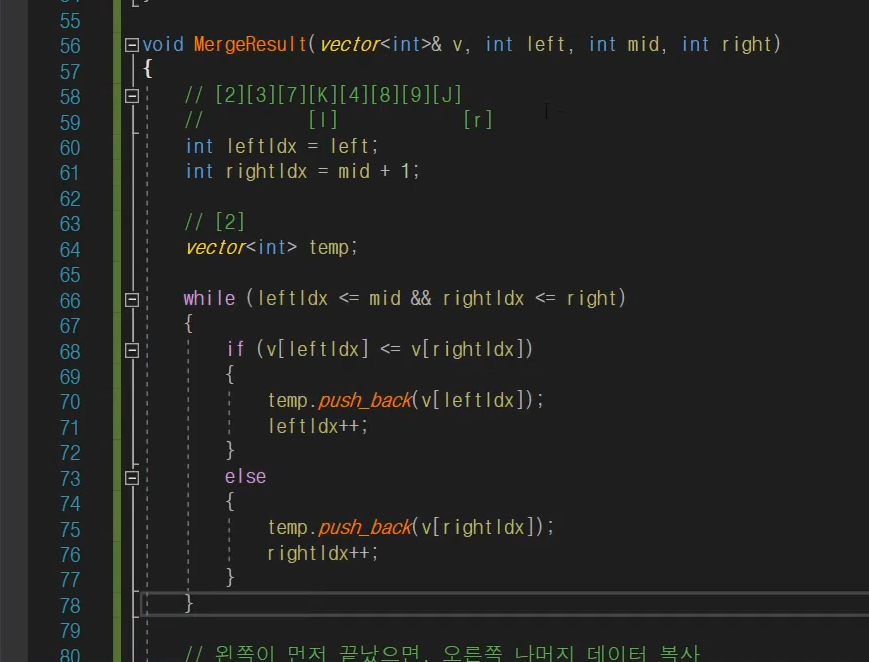
데이터가 N개 있을 경우

MergeResult를 보면은 N번씩 데이터를 비교를 한다.

그래서 일단 기본적으로 O(N)이다.

그런데 합치는 부분

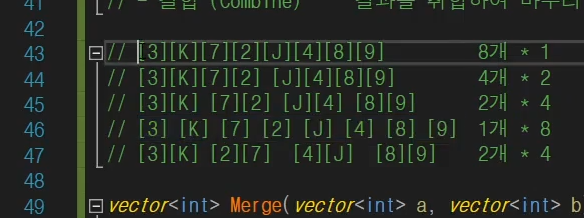
을 한번만 하고 끝내는게 아니라 O(log N)번 하기때문에

O(N log N)이다.

코드(재귀함수) 분석 ❗❗

// O(NlogN)
void MergeResult(vector<int>& v, int left, int mid, int right)
{
    int leftIdx = left;
    int rightIdx = mid + 1;

    vector<int> temp;

    cout << "Left : " << left << " " << "Mid : " << mid << " " << "Right : " << right << " " << "에 대해서 Merge 중!" << endl;

    while (leftIdx <= mid && rightIdx <= right)
    {
        if (v[leftIdx] <= v[rightIdx])
        {
            temp.push_back(v[leftIdx]);
            leftIdx++;
        }
        else
        {
            temp.push_back(v[rightIdx]);
            rightIdx++;
        }
    }

    // 왼쪽이 먼저 끝났으면, 오른쪽 나머지 데이터 복사
    if (leftIdx > mid)
    {
        while (rightIdx <= right)
        {
            temp.push_back(v[rightIdx]);
            rightIdx++;
        }
    }
    // 오른쪽이 먼저 끝났으면, 왼쪽 나머지 데이터 복사
    else
    {
        while (leftIdx <= mid)
        {
            temp.push_back(v[leftIdx]);
            leftIdx++;
        }
    }

    for (int i = 0; i < temp.size(); i++)
        v[left + i] = temp[i];
}

void MergeSort(vector<int>& v, int left, int right)
{
    if (left >= right)
        return;

    int mid = (left + right) / 2;

    cout << "Left : " << left << " " << "Mid : " << mid << " " << "Right : " << right << " " << "에 대해서 진행!" << endl;

    MergeSort(v, left, mid);
    MergeSort(v, mid + 1, right);
    MergeResult(v, left, mid, right);
}


int main()
{
    std::vector<int> vec;
    vec.push_back(30);
    vec.push_back(90);
    vec.push_back(80);
    vec.push_back(40);
    vec.push_back(70);
    vec.push_back(60);
    vec.push_back(10);
    vec.push_back(50);
    vec.push_back(20);
    vec.push_back(100);

    MergeSort(vec, 0, vec.size() - 1);
}

코드를 분석을 해보자면은

최초로 호출을 하면 이런 상태이다.

이후

MergeSort(v, left, mid);

// left = 0, mid = 4를 넘겨준다.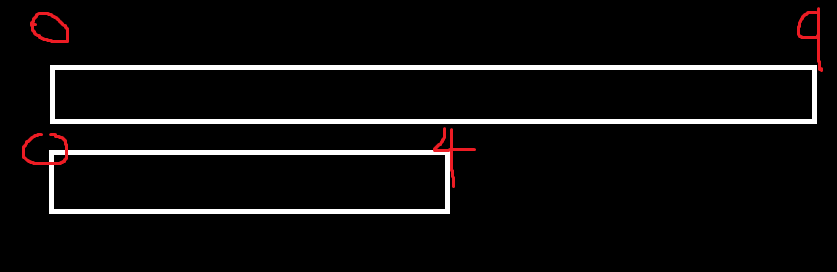

이렇게됨. 그리고 이 과정을 쭉 반복을해서

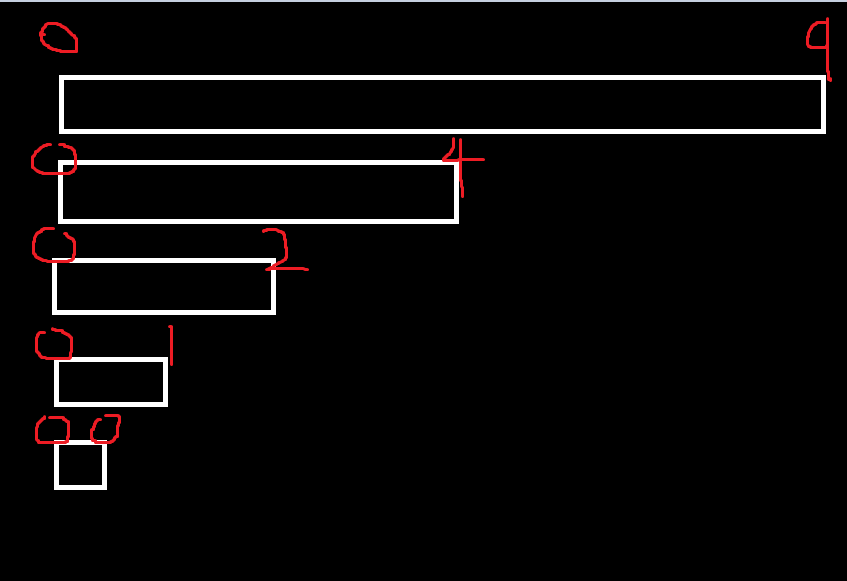
이까지 내려온다. 이후 MergeSort함수의 if (left >= right)의 조건에 걸려서 return; 하게됨.

그러면 스택 메모리에서 메모리가 날라가게 되고

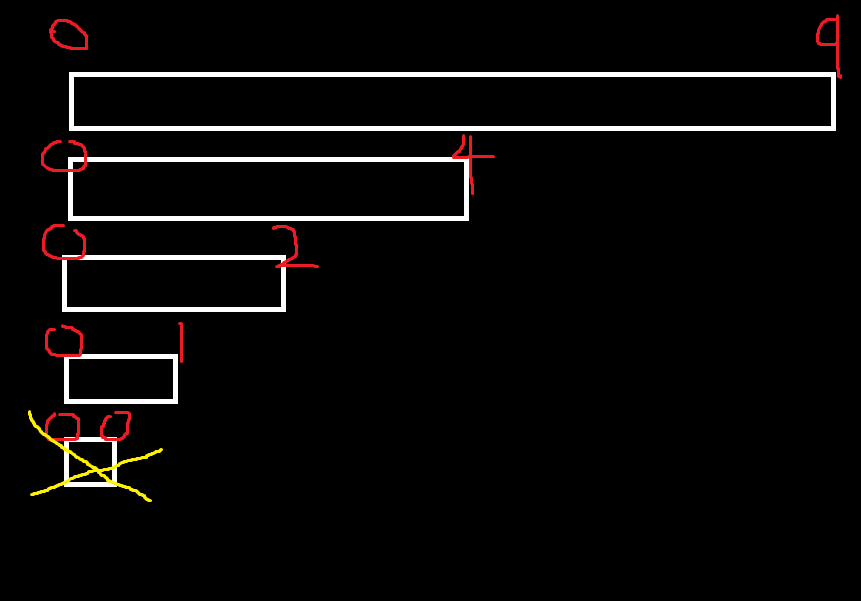
이런상태임. 그러면 left = 0, right = 0을 호출한 메모리인 left = 0, right = 1을 호출한 부분으로 돌아가

MergeSort(v, left, mid);
//  left = 0, right = 1을 호출한 부분종료됨.

MergeSort(v, mid + 1, right); // <= 호출 하러감.
MergeResult(v, left, mid, right);
}

두번째 MergeSort를 호출하러간다. MergeSort(v, mid + 1, right);

또 하나로 되었기 때문에 바로 return;을 하고

left = 0, right = 1일 경우 정렬이 끝난 부분과

left = 2, right = 2인 부분의 Merge를 진행을 한다. => 이후 정렬이 끝나면

메모리는

이런 상태인 것을 알 수 있다.

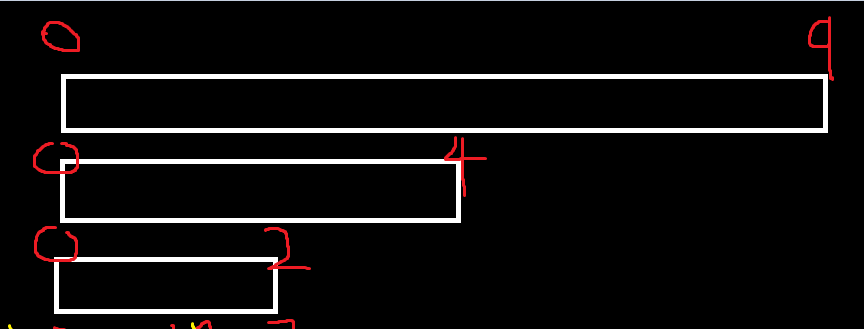
이상태로 돌아와서 현재 스택에는

left = 0, mid = 2, right = 4인 상태로 왔기 때문에

이부분 호출하러감 그리고 다시 타고타고 들어가서 데이터가 안쪼개질 때가지 들어감

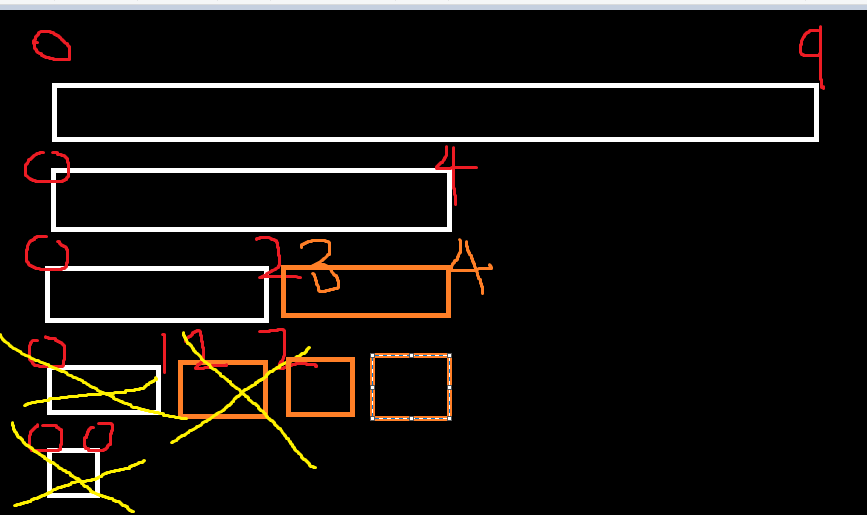
이까지 온다음에

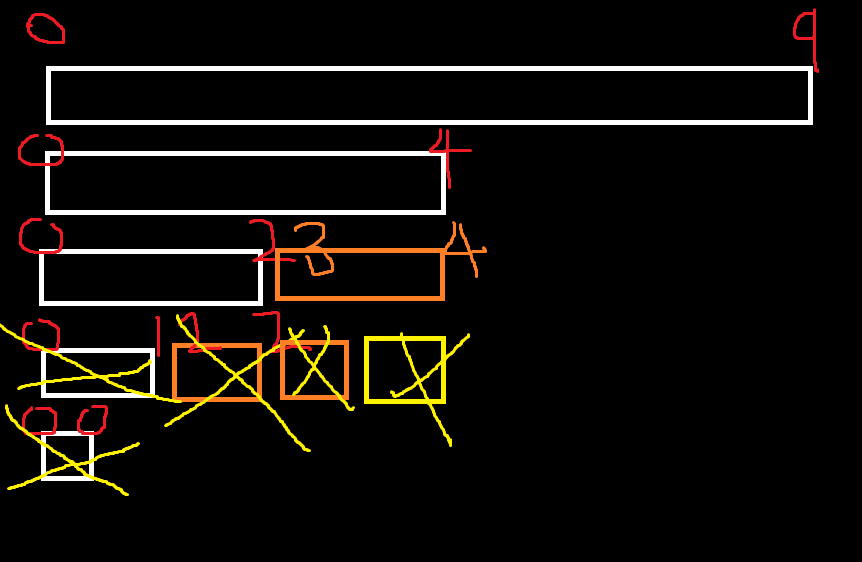
호출 종료가 되었기 때문에

left = 3, right 4인경우에 대해서 Merge를 진행을 해준다.

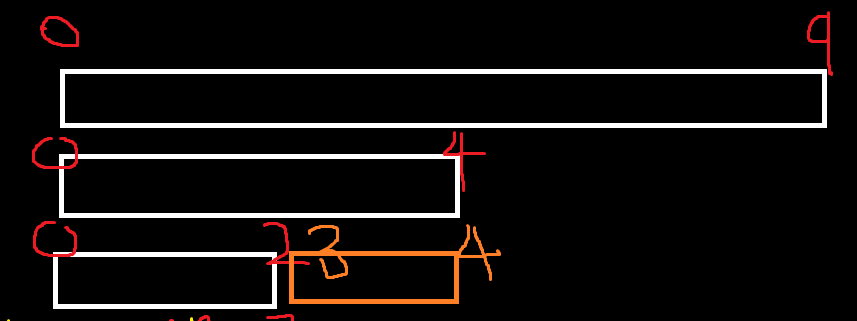
그러면 0 ~ 2, 3 ~ 4는 현재 각각 정렬된 상태에서

Merge를 호출을 해준다. Merge가 끝나고 나면은

메모리가 해제가 된다. 0~4까지는 정렬이 다 된 상태에서

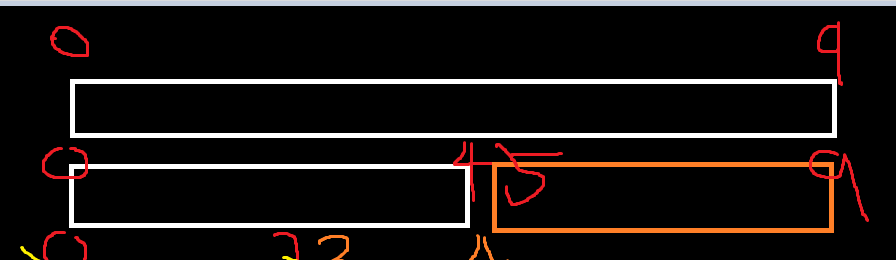
이렇게 호출 하러 간다.

즉 최초에 호출된 MergeSort에서

1 ) MergeSort(v, left, mid);


2) MergeSort(v, mid + 1, right);

MergeResult(v, left, mid, right);
}

1) 번의 작업이 다 끝나서 2)번으로 간다고 볼 수 있겠다.

출력 결과를 보면은

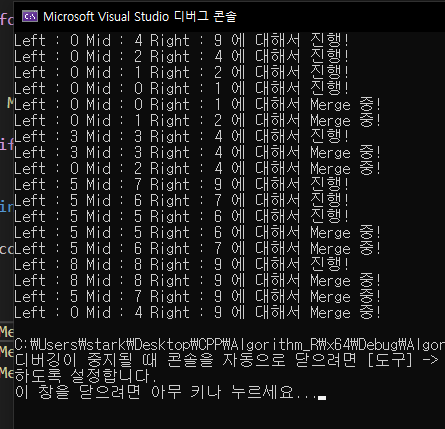
left : 0, mid : 4, right : 9에대해서 진행하고

0, 2, 4

0, 1, 2

0, 0, 1

이런식으로 갔다가 Merge하는 것을 볼 수 있다.

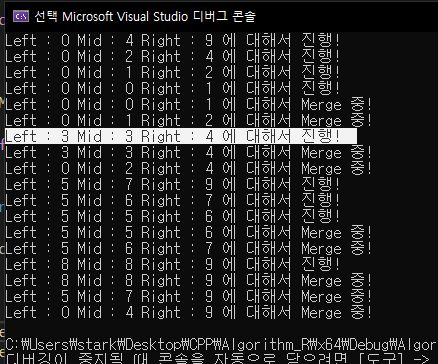
이후 left : 4, mid : 4, right : 4에 대해서 MergeSort를 진행하고 Merge하고 이렇게 재귀적으로 반복을 한다.

테스트 문제 👍👍👍

서로 정렬된 두 벡터를 다시 정렬하여 return 할 수 있도록 하는 문제.

// 이미 정렬이 되어있는 vec1, vec2를 하나의 벡터에 정렬된 상태로 만들어라.
vector<int> MergeFunc(vector<int>& vec1, vector<int>& vec2)
{
    vector<int> temp;

    int leftVecIdx = 0;
    int rightVecIdx = 0;      // vec2의 시작 Idx

    int leftVecMaxIdx = vec1.size() - 1;
    int rightVecMaxIdx = leftVecMaxIdx + vec2.size();

    temp.reserve(vec1.size() + vec2.size());
    
    while (leftVecIdx <= leftVecMaxIdx && rightVecIdx <= rightVecMaxIdx)
    {
        if (vec1[leftVecIdx] <= vec2[rightVecIdx])
        {
            temp.push_back(vec1[leftVecIdx++]);
        }
        else
        {
            temp.push_back(vec2[rightVecIdx++]);
        }
    }
    
    // 먼저 빠져 나온 경우
    if (leftVecIdx > leftVecMaxIdx)
    {
        while (rightVecIdx > rightVecMaxIdx)
        {
            temp.push_back(vec2[rightVecIdx++]);
        }
    }
    
    if (rightVecIdx > rightVecMaxIdx)
    {
        while (leftVecIdx > leftVecMaxIdx)
        {
            temp.push_back(vec1[leftVecIdx++]);
        }
    }

    return temp;
}

결과는 잘 나온다. 병합정렬 개념 활용한 문제임.

정리 ❗

힙정렬과 병합(합병)정렬 둘다 O (N Long N)을 가진다...

굳이 따지자면은 병합이 아주아주아주 살짝 더 빠른 정도??

힙정렬은 우선순위 큐를 통해 빠르게 구현할 수 있었다. 이해하기도 좀 쉽고... (물론 우선순위 큐까지 구현을 하라고 하면 시간이 더 걸림..)

다만 병합 정렬에서

재귀적으로 타고 들어가서 나누고 병합하는 부분

눈여겨서 보고 분석을 다시 해야할 거 같다.