
1. 레드 블랙 트리 구현 방법
균형 맞추는 알고리즘 많음.
AVL, Trick, 레드 블랙 트리 => 싹다 균형맞추는 알고리즘임.
2. 레드블랙 트리 특성

NIL은 그냥 Dummy 노드임.
4번 특성이 중요함.
레드 -> 레드 안됨. 블랙 -> 블랙 -> 블랙 이런거는 되지만.
아무튼 1~5번 특성 위반되면은 재구성이 발생함.
레드 블랙 트리는 새로 추가하는 노드는 항상 RED이다.
3. Fix
균형 맞출때 경우가
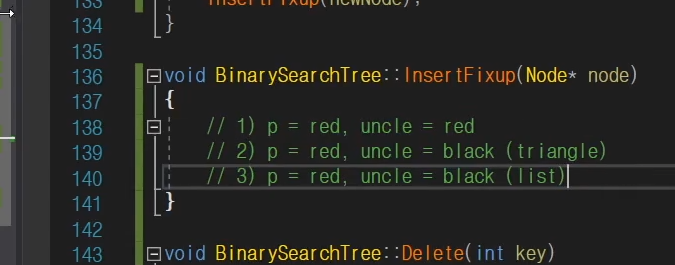
이 세가지가 있음.
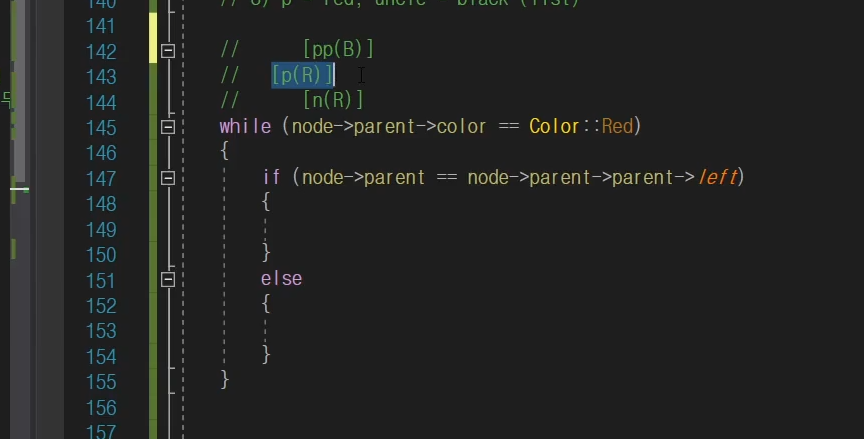
이거 시발 말이 좀 어려운데 node->parent가 node->parent->parent의 왼쪽 자식으로 있을 경우 말하는거임.
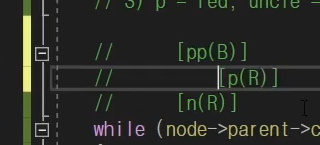
else는 pp의 오른쪽 자식일 경우 말한다.
4. Rotate
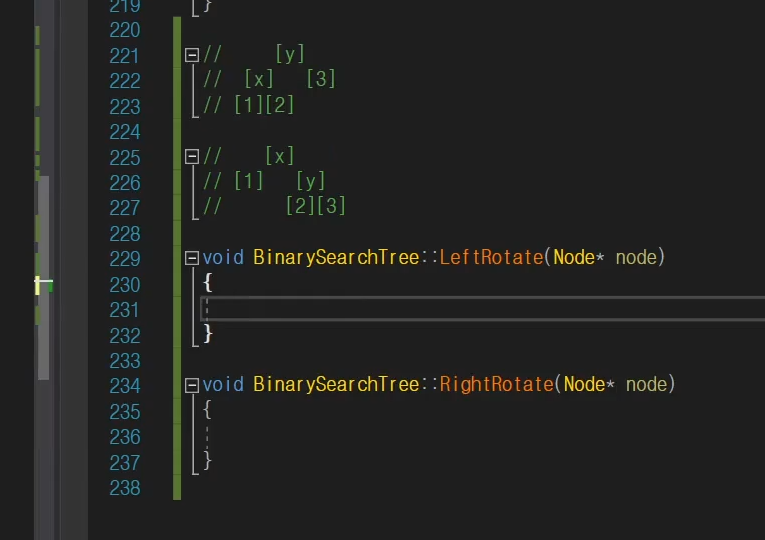
지금 저 상황을 곧이 곧대로 만들어 볼 것이다.
5. Fixup 함수 분석
1) p = red, uncle = red
- p = black, uncle = black, pp = red로 바꾼다.
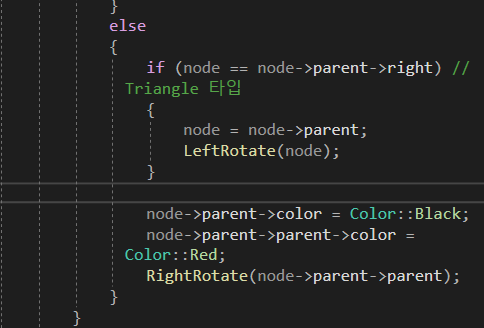
2) p = red, uncle = black (triangle)
- 회전을 통해 case 3으로 바꿈
3) p = red, uncle = black (list)
- 색상 변경 + 회전
while문 시작
30, 10, 20, 25, 40, 50 순으로 넣을 것임.
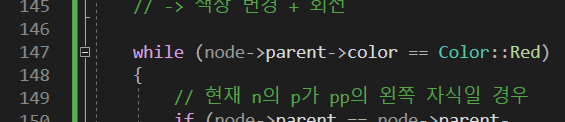
node->parent->color가 RED가 아닐 경우 못들어옴.
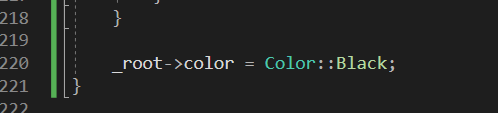
바로 빠져나와서 Black으로 바뀜.
즉, root node집어 넣을 경우 BLACK으로 바로 바뀌고 나옴.
그다음 10넣을 경우
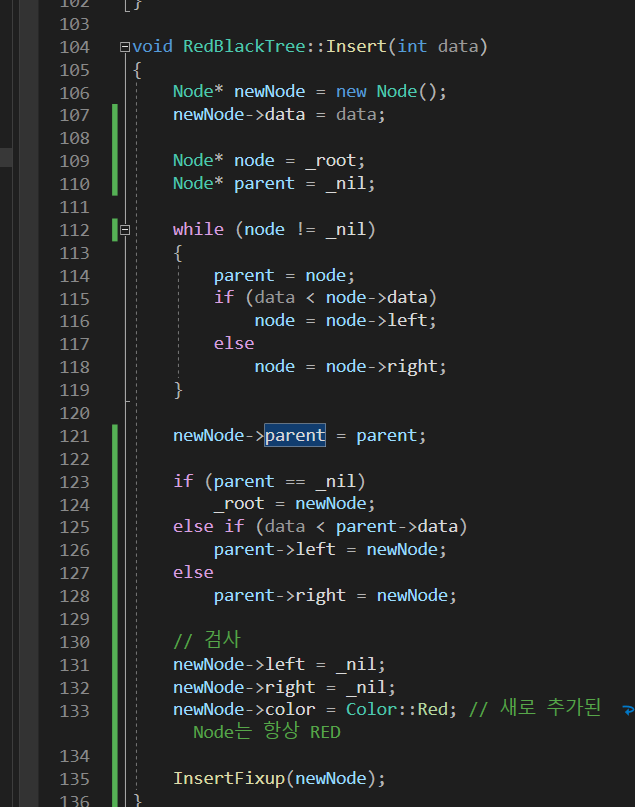
Insert부분에서 이러이러한 코드에 의해 root의 왼쪽 자식이 됨.
현재 InsertFixup들어가기전에는 RED임.
들어가면 while문의 조건에 맞지 않아서 while문 안들어감.
그리고나서 10은 빨강색임.
20을 넣으면은 현재 30이 root이고 b
10은 root의 left이고 r인 상태임.
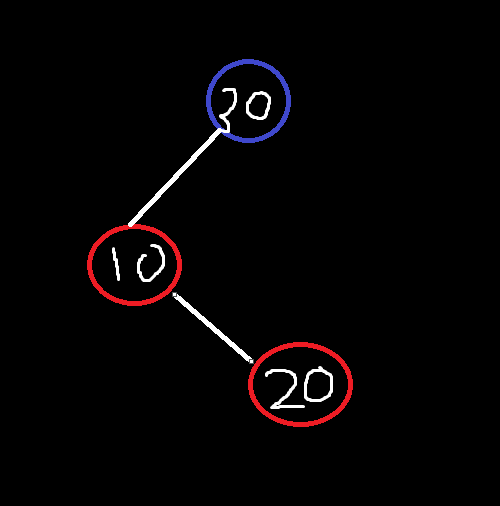
현재는 이런상태임.
20은 10이 부모이고 right에 r인 상태로 InsertFixup들어옴.
while문 조건을 보면은 node->parent->color == RED이기 때문에 들어옴.

먼저 첫번째 if문 조건 확인하는데 20의 p가 pp의 왼쪽자식이라 들어온다.
uncle만드는데 node->pp는 _nil인데
Node의 기본 Color가 BLACK이라
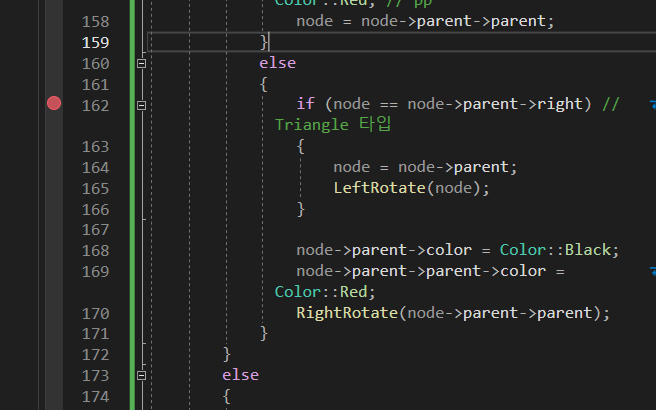
else로 빠짐.
그리고 node가 p의 right가 맞기 때문에 왼쪽으로 회전시킴.
이게 레드블랙트리임.
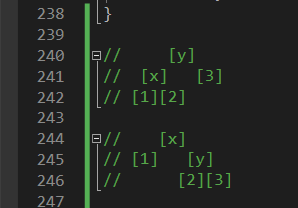
현재 이 그림대로 하면 됨.
현재 LeftRotate에 20의 p인 10이 들어옴.

현재여기서 x가 10이라는건데...
y가 20임
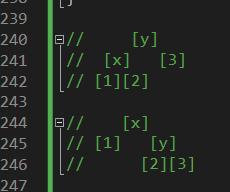
이게 지금
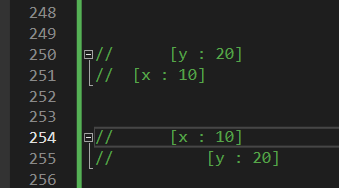
이렇게 만들어라는 말같음.
그러면
void RedBlackTree::LeftRotate(Node* x)
{
Node* y = x->right;
// x->right인 20이 y가됨
x->right = y->left;
// y->left인 _nil이 x->right로 들어감
// 왼쪽 자식의 부모를 로
if (y->left != _nil)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == _nil)
_root = y;
else if (x == x->parent->left) // x가 부모의 왼쪽 자식일 경우
x->parent->left = y;
else
x->parent->right = y; // x가 부모의 오른쪽 자식일 경우
y->left = x;
x->parent = y;
}쭉 실행이 끝나면은
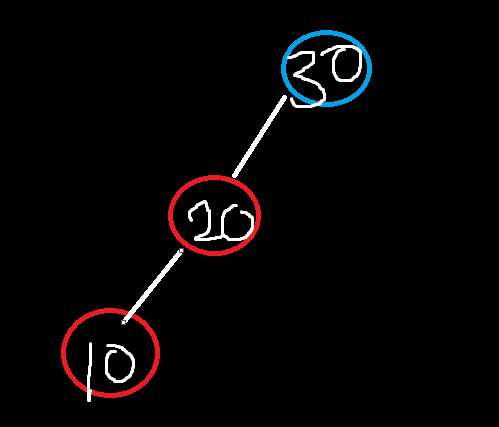
이런 상태이다.
그리고

이까지 실행하면
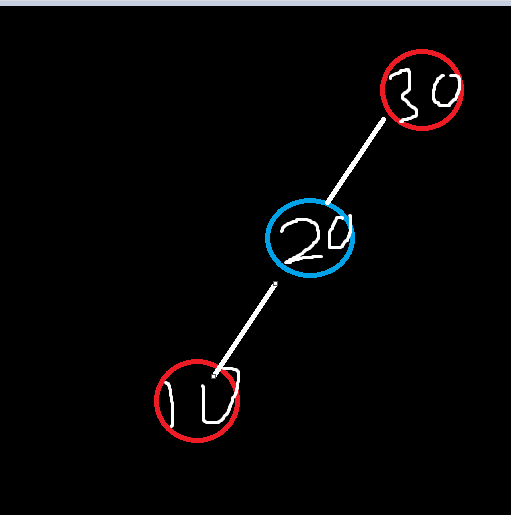
이럼.
그리고 RightRotate에 30넣음.
왜? Triangle나왔으니까
회전을 통해서 list로 바꾸고
색상변경 및 회전을 해주는거임.
void RedBlackTree::RightRotate(Node* y)
{
Node* x = y->left;
y->left = x->right;
if (x->right != _nil)
x->right->parent = y;
x->parent = y->parent;
if (y->parent == _nil)
_root = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
x->right = y;
y->parent = x;
}이까지하면은
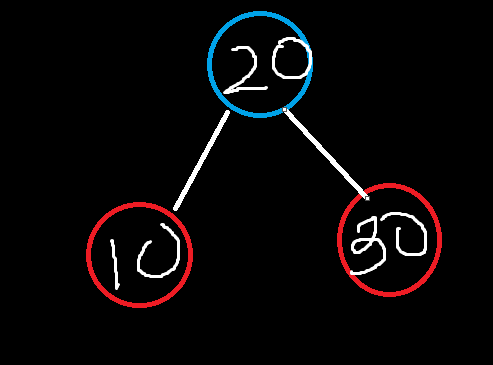
이렇게 됨.
실행결과보면 이렇게 나옴.
5. Delete ❗
BST삭제를 보면은
1) 삭제할 노드가 자식이 없는 경우
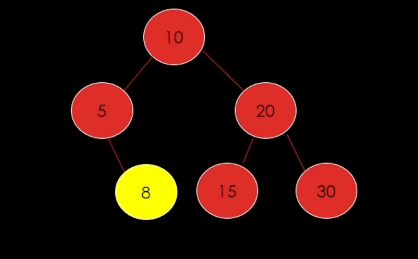
이때는
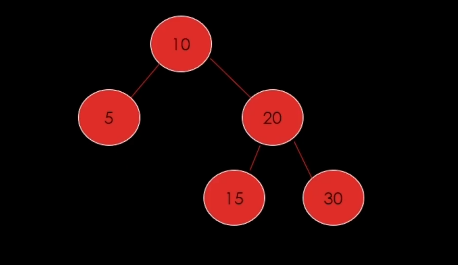
그냥 삭제하면된다.
2) 삭제할 노드가 자식이 1개인 경우
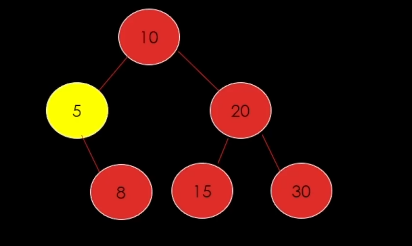
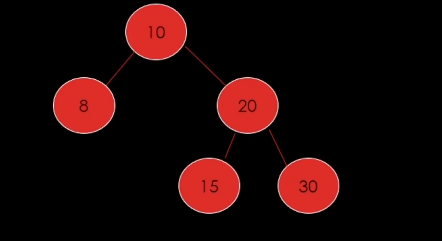
이렇게 되어야함.
3) 삭제할 노드가 자식이 2개인 경우

삭제할 노드의 다음 노드를 중위순회로 찾은다음에
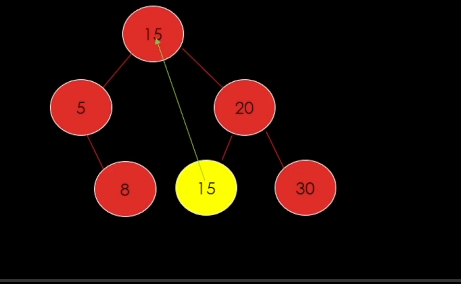
다음 노드의 데이터를 올려보내고 다음 데이터를 삭제를 한다.
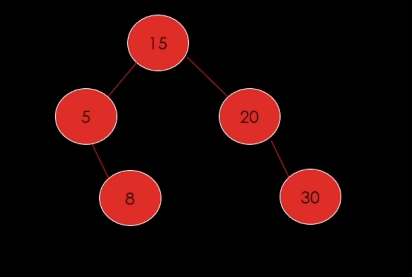
이렇게됨.
Red Black Tree잠깐 보면은
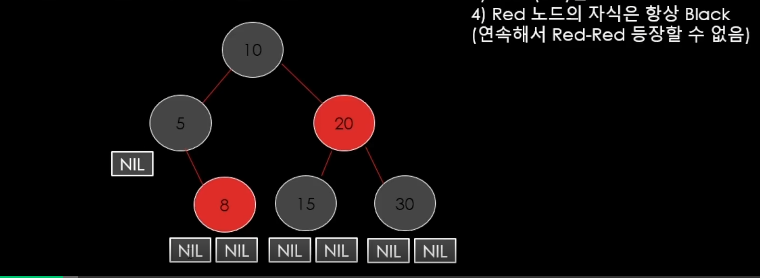
이런식으로 되어 있다.
6. Red-Black Tree Delete ❗
case 1 : 삭제할 노드가 Red인 경우
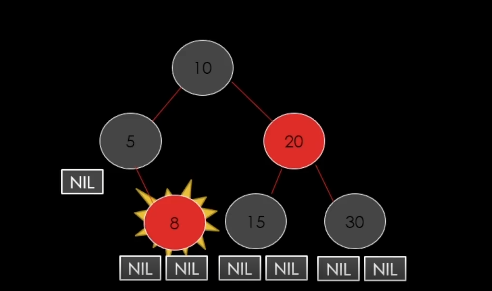
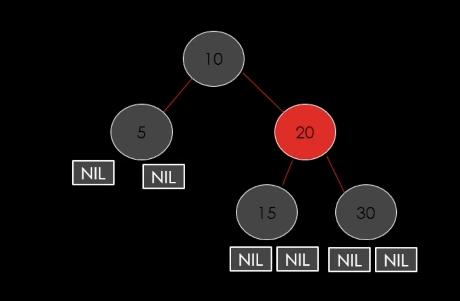
그냥 삭제하면 됨.
case 2 : 삭제할 노드가 Black일 경우
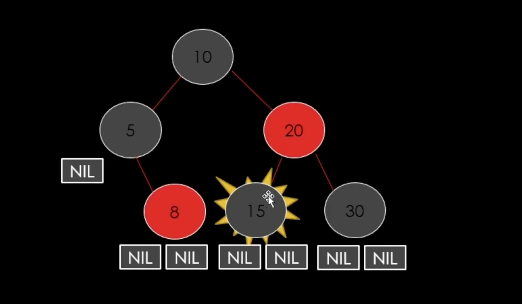
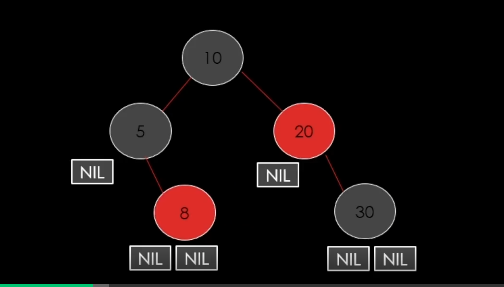
이렇게 삭제만 하면되는데 문제가 발생을 한다.

레드 블랙트리는 이 5가지 조건을 만족을 해야하는데,

이상황은 5번을 위배함.
리프노드에서 root까지 가는데 Black이 root하나밖에 없음 다른 애들은 두개라서.
그래서 어떻게든 블랙갯수를 맞추는 노가다 작업을 한다고 보면은 된다.
그래서 이다음에
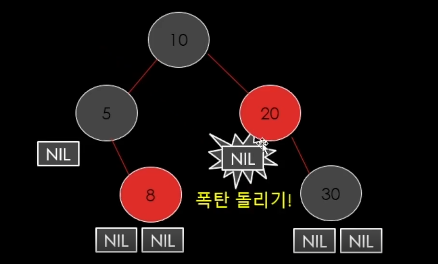
가상의 Black이 하나 더잇다고 생각을 하자
=> 조금 있어보이는 말로는 "Double Black"이라고한다.
아무튼 이 double black인 상태에서 일종의 폭탄 돌리기를 해야된다.
이 추가적인(가상의 Black)을 누군가가 가져가가지고
트리의 균형을 맞추어야한다.
(단순 하지는 않다)
근데, 여기세어도 똑똑한 사람들이 공식을 다 만들어 놓음.
나 같은 좆밥은 나와있는 공식을 그대로 쓰기만 하면된다! 굿.
근데 그 공식이 6개가 있는데 다 암기할 필요는 없다! ㅎㅎ!
case 3 : 삭제할 노드가 Root일 경우
Root가 Double Black일 경우 추가적인 Black삭제하고 끝임.
삭제할 노드가 Black일 경우 "형제 노드"가 자주 등장 할 것임.
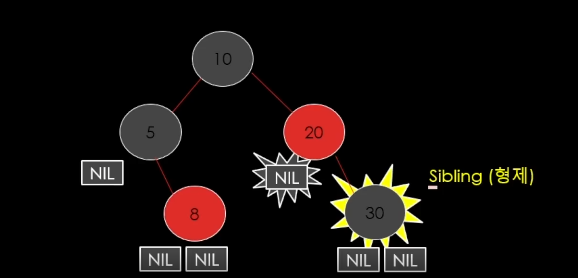
삭제할 Black노드의 형제노드의 색에 따라서 알고리즘이 갈린다.
레드 블랙 트리 삭제 알고르즘에서는
Double Black의 형제 노드가 핵심이다.
Sibling의 조건

형제가 어떤 조건을 가지고있는지에 따라서 로직이 달라진다.
형제가 Red일 경우 조절 하기가 까다롭다.
일단 이 Red일 경우 검정색으로 만들려고 노력을 할 것이다.
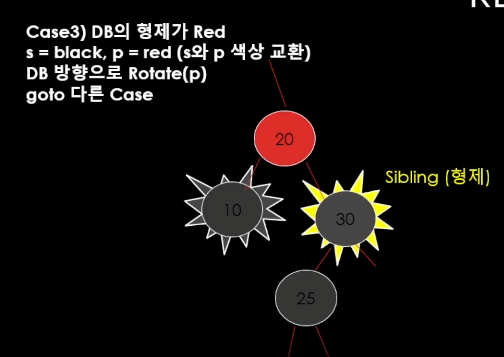
이 다음에 DB의 방향으로 LeftRotate를 해준다.
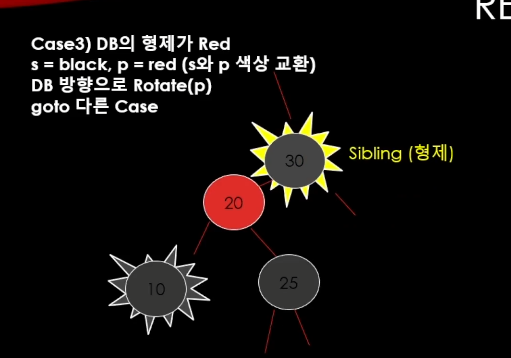
LeftRotate하면 이렇게 됨.
그다음에 DB의 형제를
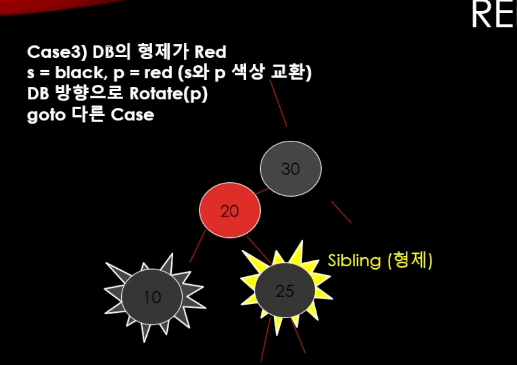
25로 바꾼다. => 계속 로직 실행을 한다.
(다른 로직을)
case 4 :


case 5
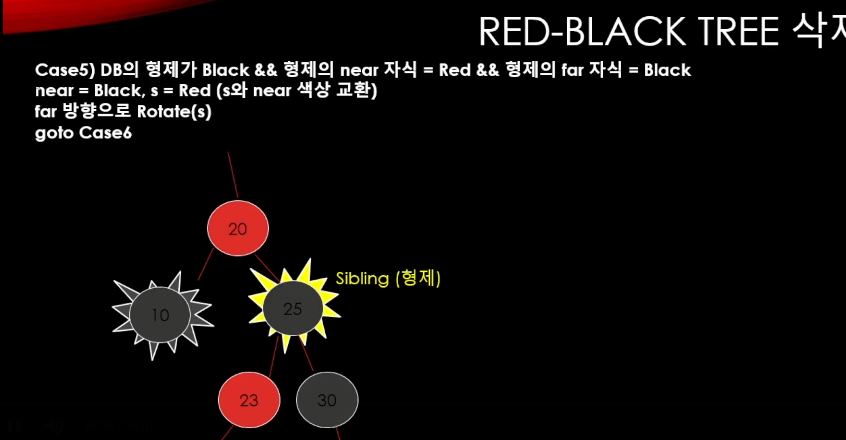
이럴경우
near = 23, far = 30임
(10 node를 기준으로 멀리있고 가까이 있는거라고 생각하면됨.)
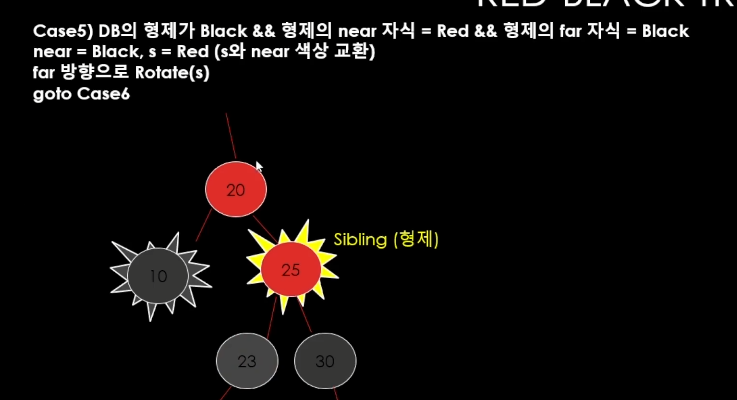
색을 바꿔준다음에

색을 바꾼 다음에 far방향으로 Rotation을 진행을 한다.

원래는 near = b, far - b 인 상태에서
near = b, far = r로 바꾼것임.
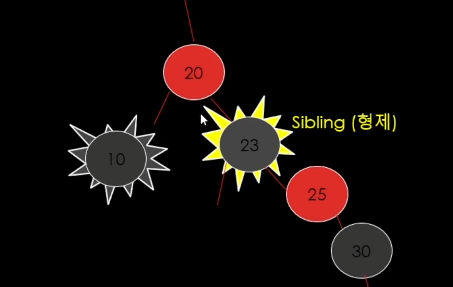
이상황이 오는데 => case 6으로 간다.
case 6

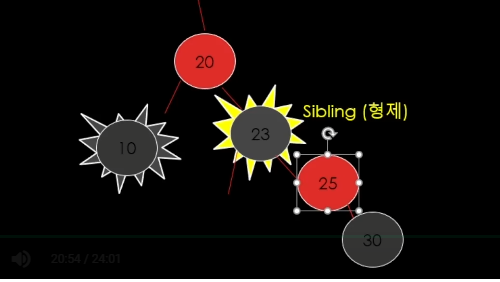
이 경우임.
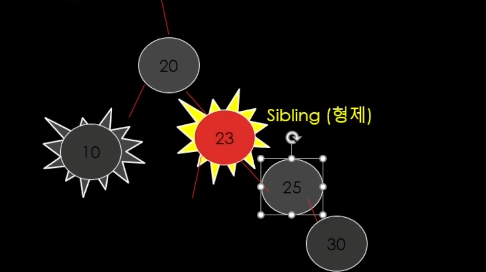
이렇게 p <-> s 색 바꾼다.
DB방향으로 Left회전함.
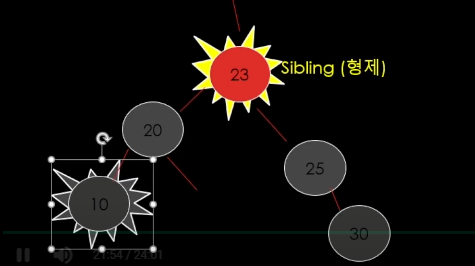
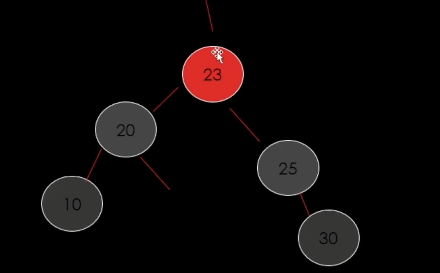
규칙을 달달달 외워서 규칙에 맞게 코드를 짜면은 됨.
참고 ❗
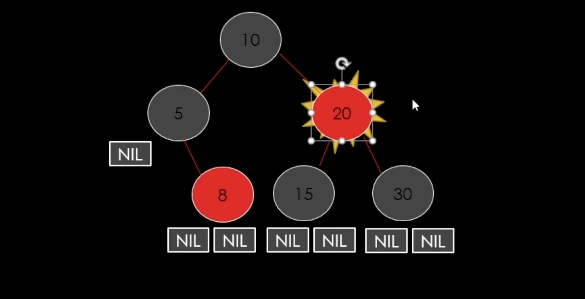
Delete할 node가 Red일 경우가 쉽다고 했었는데 그것은
맨 마지막에오는 8같은 leaf노드일 경우를 말하는 것이다.
20의 경우는 아니다. =>
BST로 예를 들면은 20을 바로삭제를 하는게 아니라
20의 다음 노드를 구한다 (30)
30의 데이터를 20으로 복사 하고 30이 있던 노드를 삭제를 하는 것이다.
그래서 만약 20이라는 RED노드를 삭제를 한다고했을 때,
BST와 비슷하게
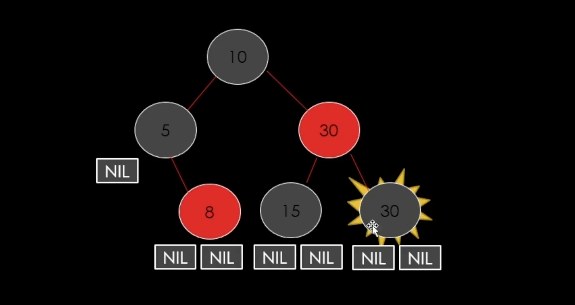
사실상 Black노드를 삭제한다고도 볼 수 있는 것이다.
삭제에서 중요한? 부분
이것을 실전에서는 구현을 못한다 너무 복잡해서
다만 중요한 것은 대략적으로 어떻게 동작을 하는지는 알고있어야한다.
즉, 삭제를 할 때 기존의 레드블랙트리의 규칙이 깨지기 때문에 규칙을 맞추기 위해서
지랄한거임.
블랙노드를 삭제를 할경우 블랙노드의 수가 모자르기 때문에
삽입의 경우 uncle 노드가 중요하고
삭제를 할 때는 형제노드인 DB의 Sibling이 핵심적인 역할을 맡는것이다.
