비재귀 세그먼트 트리 (C++, Python)

비재귀 세그먼트 트리

필자는 세그먼트 트리 자료구조를 처음 접했을 때 2번 놀랐다. 첫 번째로는 이걸 어떻게 생각해냈을까, 두 번째로는 이 많은 코드를 어떻게 다 쓰지?였다. 재귀로 세그먼트 트리를 구현하기 위해서는 생각보다 많은 코드가 필요했다. C++ 재귀 구현 코드는 아래의 링크에 아주 자세한 설명과 함께 구현이 되어 있다.

[세그먼트 트리 재귀 구현]
https://book.acmicpc.net/ds/segment-tree

한 동안 재귀 구현 코드로 문제를 풀어오다 비재귀적으로 구현한 코드는 없을까하고 검색했고 아주 좋은 글을 발견했다.
https://blog.joonas.io/129

위의 블로그에서 Codeforces에서 누군가 7년 전(!!)에 적은 비재귀 구현에 대하여 설명한 포스트를 발견했다.
https://codeforces.com/blog/entry/18051

설명이 아주 자세하게 되어있지만 영어라 읽기 부담스러운 독자가 있을까봐 간략하게 번역 및 소개를 하려고 한다. 참고로 lazy propagation 역시 비재귀로 구현되어 있으니 관심 있다면 한 번 직접 들어가서 읽어보길 바란다.

기존 재귀 구현과의 차이점을 비교하며 설명하려고 한다.

트리 크기

재귀 구현의 경우 주어진 원소의 개수(N)보다 크면서 가장 작은 2의 제곱수만큼 트리의 원소 개수가 필요하다. 편의상 tree를 t로 표현하겠다.

// 재귀 구현 시, 트리 크기
int N = 100000;

int h = (int)ceil(log2(N));
int tree_size = 1<<(h+1);
int t[tree_size];

// or

int t[4*N];

위와 같이 N보다 크면서 가장 작은 2의 제곱수만큼을 할당해줘도 되고, 간단하게 4배만큼 할당해줘도 된다.

비재귀 구현의 경우 2*N의 크기만큼 트리의 크기를 할당하여 주면 된다.

// c++
// 비재귀 구현 시, 트리 크기
int N = 100000;
int t[2*N];

# python
N = 100000
t = [0 for i in range(2*N)]

2배만큼 할당받는 이유는 인덱스 N~(2N-1)까지는 입력으로 들어오는 숫자를 넣고, 인덱스 1~(N-1)까지는 트리의 노드로 구성되기 때문이다.

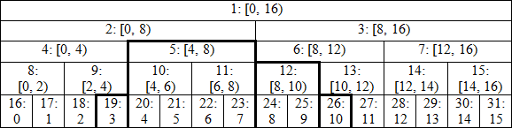
예시 사진의 경우 원소의 개수가 16개인 비재귀 세그먼트 트리 구현을 도식화한 그림이다. 인덱스 16~31까지 입력으로 들어오는 원소들의 인덱스가 쓰여있고, 1~15까지는 범위를 나타내는 노드로 구성되어 있다.

범위 포함 관계 [l,r)

재귀 구현의 경우 [l,r]의 방식으로 left와 right가 모두 포함되는 범위로 구성된다.
비재귀 구현의 경우 가장 주의해야 하는 부분이 [l,r)로 left는 포함, right는 미포함이라는 점이다. 비재귀 구현에서 인덱스 문제로 헷갈릴 수 있는 가능성이 있기 때문에 오른쪽은 절대 미포함이라는 사실을 항상 기억해야 한다. 이 점을 유념하며 트리 초기화 코드를 살펴보자.

초기화

// c++
void init() {
	for(int i=N-1;i>0;--i) t[i] = t[i<<1] + t[i<<1|1];
}

# python
def init():
	for i in range(N-1,0,-1): t[i] = t[i<<1] + t[i<<1|1]

이 코드를 처음 본 필자의 소감:
????????????????????

필자의 같은 소감을 가졌다면 천천히 다시 생각해보자. 초기화 코드에서 우리가 왜 입력받을 때 인덱스 N~(2N-1)에 입력 받았는지 알 수 있다. 부모 노드는 /2 를 통해 올라간다는 점을 이용하여 bottom-up 방식으로 구현하기 위해 그랬던 것이다.
i<<1 은 2를 곱해주는 연산이며 i<<1|1은 2를 곱하고 1을 더해주는 연산과 같다. 따라서 i = N-1 일 때, i = 2*N-2 , i = 2*N-1 인 왼쪽 자식과 오른쪽 자식 노드의 값을 더하여 부모 노드의 값으로 설정한다.

i = N-1,
t[i] = t[i<<1] (왼쪽 자식) + t[i<<1|1] (오른쪽 자식)

그렇게 i = 1 까지 거꾸로 올라가며 범위를 채워나간다.

수정

// c++
void update(int p, int value) {
	for(t[p+=N] = value; p>1; p>>=1) t[p>>1] = t[p] + t[p^1];
}

# python
def update(p,val):
	p += N
	t[p] = val
	while p>1:
		t[p>>1] = t[p] + t[p^1]
		p>>=1

????????????????
2차 멘붕이 온다.

위에서 한 번 당했기 때문에 그래도 조금은 이해할 수 있을 것 같다. 눈치가 빠른 분들은 눈치챘을 것 같다. i번째 입력의 트리에서 인덱스는 i+N이 된다. 따라서 입력을 받을 때 N부터 받은 또 다른 이유이기도 하다.

arr = {0,1,2,3};
t = { xxx, [0,4), [0,2), [2,4), 0, 1, 2, 3};

이와 같이 트리가 생성되게 된다. 만약 여기서 1을 수정하고 싶다면 트리에서는 t[1+4]가 수정되어야 한다. 그걸 나타낸 부분이 바로 t[p+=N] = value; 이다.

leaf node의 값을 수정하였으면 재귀 구현과 비슷하게 해당 노드를 포함하는 구간의 노드의 값을 모두 수정해줘야 한다. 그 과정이 t[p>>1] = t[p] + t[p^1] 이다. 여기서 p^1을 통해 p 가 왼쪽 자식이라면 p^1 은 오른쪽 자식을, 반대로 p 가 오른쪽 자식이라면, p^1 은 왼쪽 자식을 가리키는 인덱스가 된다.

쿼리

// c++
int query(int l, int r) {
	int res = 0;
	for(l+=N,r+=N; l<r; l>>=1,r>>=1) {
    	if(l&1) res += t[l++];
        if(r&1) res += t[--r];
    }
    return res;
}

# python
def query(l,r):
	l+=N
	r+=N
	res = 0
	while l<r:
		if l&1:
			res += t[l]
			l += 1
		if r&1:
			r -= 1
			res += t[r]
		l>>=1
		r>>=1

	return res

3차 멘붕
도대체 재귀 구현에서의 그 많은 코드는 무엇을 위한 것이었단 말인가..라는 생각이 든다.

l+=N,r+=N 의 경우 이제 좀 알겠다. 인덱스 l , r 위치에 있는 입력 값을 가진 leaf node를 찾아가는 연산이다. l<r 도 왼쪽 범위가 오른쪽 범위보다 작아야 하니까 그렇고, l>>=1,r>>=1 도 트리에서 노드의 인덱스가 /2씩 작아지니까 그런 것도 이제 알겠다.

그렇다면

if(l&1) res += t[l++];
if(r&1) res += t[--r];

이 부분은 도대체 뭐란 말인가!

아래의 사진을 다시 한 번 보자. 아래의 사진은 N = 16 이고, [3,11) 의 범위의 합을 구하는 과정이다.

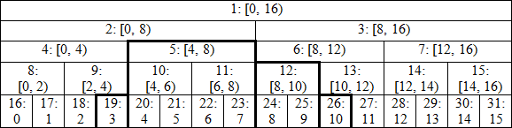
우선 if(l&1) 의 뜻은 l이 홀수일 때를 뜻한다. l 이 홀수일 때(위의 그림에서는 l=3), 해당 노드의 값은 /2를 해서 올라오게 되는 다음 부모 노드의 범위에 속하지 않는다. 따라서 결과에 해당 노드의 값을 더해주고 +1이 된 후, /2로 상위 노드로 올라간다.

l 이 짝수라면, 상위 노드가 그 값을 포함하고 있기 때문에 하위 노드에서는 더해주지 않고 /2를 통해 바로 상위 노드로 올라간다.

반대로 if(r&1) 의 뜻은 r 이 홀수일 때를 뜻한다. r 은 범위에 해당되지 않기 때문에([l,r)), r 이 홀수일 때, -1을 하고 해당 노드의 값을 더한 후, /2로 상위 노드로 올라간다.

r 이 짝수라면, 일단 범위에 포함되지 않기 때문에 -1을 해주게 되면, 더 이상 하위 노드에서는 범위 안에 속하지 않게 되기 때문에 /2를 통해 상위 노드로 올라간다. [3,10)의 범위를 예시로 생각해보면 이해가 빠를 것 같다.

예시와 같이 perfect binary tree 일 때, 저렇게 예쁘게 착착착 바로 이웃한 범위와 짝을 맞춰 올라가게 되며, perfect binary tree가 아닐 경우에는 이웃하지 않은 범위와 짝을 맞춰 올라가게 됨을 알아두자.

C++ 코드

비재귀

#include <bits/stdc++.h>

using namespace std;


const int N = 1e6;
int t[2*N];

void init() {
	for(int i=N-1;i>0;--i) t[i] = t[i << 1] + t[i << 1 | 1];
}

void update(int p, int val) {
	for(t[p+=N] = val; p > 1; p >>= 1) t[p>>1] = t[p] + t[p^1];
}

// [l,r)
int query(int l, int r) {
	int res = 0;
	for(l+=N, r+=N; l < r; l >>= 1, r >>= 1) {
		if(l&1) res += t[l++];
		if(r&1) res += t[--r];
	}
	return res;
}

재귀

#include <bits/stdc++.h>
#define mid = (st+end)/2

using namespace std;

const int N = 1e6;

int arr[N+1];
int tree[4*(N+1)];

void init(int node, int st, int end) {
	if(st == end) {
		tree[node] = arr[st];
	} else {
		init(node*2, st, mid);
		init(node*2+1, mid+1, end);
		tree[node] = tree[node*2] + tree[node*2+1];
	}

	return;
}

void update(int node, int st, int end, int idx, int val) {
	if(idx < st || idx > end) {
		return;
	}
	if(st == end) {
		arr[idx] = val;
		tree[node] = val;
		return;
	}
	update(node*2, st, mid, idx, val);
	update(node*2+1, mid+1, end, idx, val);
	tree[node] = tree[node*2] + tree[node*2+1];

	return;
}

int query(int node, int st, int end, int left, int right) {
	if(left > end || right < st) {
		return 0;
	}
	if(left<=st && end<=right) {
		return tree[node];
	}

	int lsum = query(node*2,st,mid,left,right);
	int rsum = query(node*2+1,mid+1,end,left,right);
	return lsum + rsum;
}

Python 코드

비재귀

N = 1e6
t = [0 for i in range(2*N)]

for i in range(N,2*N):
	t[i] = int(input().rstrip())

def init():
	for i in range(N-1,0,-1): t[i] = t[i<<1] + t[i<<1|1]

def update(p,val):
	p += N
	t[p] = val
	while p>1:
		t[p>>1] = t[p] + t[p^1]
		p>>=1

def query(l,r):
	l+=N
	r+=N
	res = 0
	while l<r:
		if l&1:
			res += t[l]
			l += 1
		if r&1:
			r -= 1
			res += t[r]
		l>>=1
		r>>=1

	return res