[프로그래머스] 양과 늑대

[프로그래머스] 양과 늑대
https://programmers.co.kr/learn/courses/30/lessons/92343

풀이

트리의 간선을 따라 노드를 탐색하는 문제처럼 보였다면 절반은 맞췄다고 할 수 있다. 문제는 완전탐색을 구현할 때, 일반적인 완전 탐색과는 다르게 양을 찾는 경로를 신경쓰지 않는다는 점이 달랐다.

한 번 방문한 노드에 존재하는 동물은 그 이후에 어떤 노드를 가던지 뒤를 졸졸 따라다닌다. 그 상태로 왼쪽 혹은 오른쪽 노드로 넘어갔다 돌아오는 경로가 생기기도 한다. 경로의 경우의 수를 구현하여 완전탐색을 하기엔 너무 복잡하다.

경로를 잊고, 지금까지 방문한 노드를 제외하고 다음에 방문할 수 있는 노드의 후보만 가지고 완전탐색을 구현해야 한다.

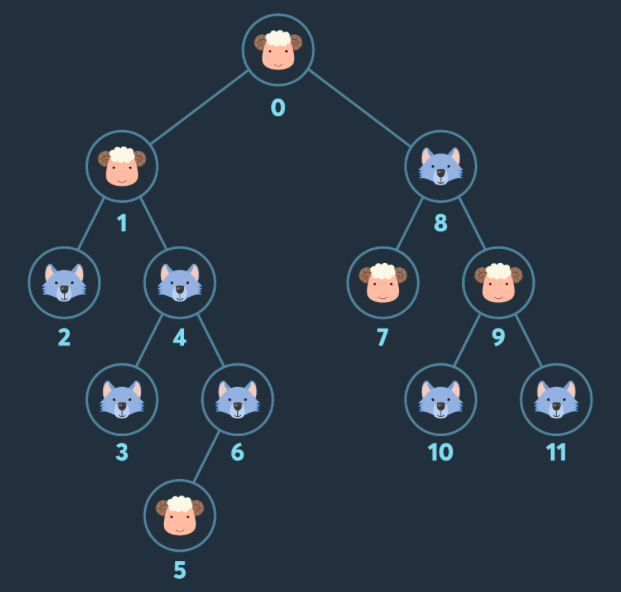
첫번째 테스트 케이스를 예시로 설명해보자면, 시작은 항상 0번 노드고 양이 존재한다. 0번 노드에서 다음 번에 갈 수 있는 노드의 후보는 {1,8}이다.
1번 노드로 가기를 선택했다고 치자. 1번 노드의 동물은 양이므로 양 최댓값을 2로 갱신한다. 1번 노드로 경로를 개척했으니 이제 다음으로 선택할 수 있는 노드의 후보는 {8,2,4}가 된다.
그 다음 8번 노드를 가기로 선택했다고 하면, 8번 노드의 동물은 늑대이므로 양의 최댓값은 여전히 2이다. 8번 노드로 경로를 개척했으니 이제 다음으로 선택할 수 있는 노드의 후보는 {2,4,7,9}이다.

이런 식으로 경로의 경우의 수는 잊고, 다음 번에 갈 수 있는 노드의 후보만 가지고 완전탐색을 진행해야 한다. 수도코드로 적어보면 다음과 같다.

dfs(currentNode, wolf, sheep, nextNodes, info) {
	if info[currentNode] == 0 then
    	sheep++
    else
    	wolf++
        
    ans = max(ans, sheep)
    
    if(wolf >= sheep) return
    
    for node in nextNodes:
    	next = (다음 번에 갈 수 있는 노드의 후보)
        dfs(node, wolf, sheep, next, info)
        
    return
}

C++ 코드

#include <string>
#include <cstring>
#include <cmath>
#include <vector>

using namespace std;

vector<vector<int>> graph;
int ans = 1;
int s = 0;
int w = 0;

void dfs(int currNode, int w, int s, vector<int> nextNodes, vector<int> info) {
    int animal = info[currNode];
    if(!animal) {s++;}
    else {w++;}
    
    ans = max(ans, s);
    
    if(w >= s) {return;}
    
    for(int i=0;i<nextNodes.size();++i) {
        vector<int> next = nextNodes;
        next.erase(next.begin()+i);
        for(int j=0;j<graph[nextNodes[i]].size();++j) {
            next.push_back(graph[nextNodes[i]][j]);
        }
        dfs(nextNodes[i],w,s,next,info);
    }
    
    return;
}

int solution(vector<int> info, vector<vector<int>> edges) {
    graph.clear();
    for(int i=0;i<info.size();++i) {
        vector<int> v;
        graph.push_back(v);
    }
    for(int i=0;i<edges.size();++i) {
        graph[edges[i][0]].push_back(edges[i][1]);
    }
    
    vector<int> st;
    for(int i=0;i<graph[0].size();++i) {
        st.push_back(graph[0][i]);
    }
    dfs(0,0,0,st,info);
    
    return ans;
}