에라토스테네스의 체(Sieve of Eratosthenes)

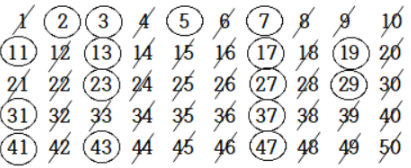
에라토스테네스의 체(Sieve of Eratosthenes)는 고대 그리스의 수학자 에라토스테네스가 고안한 소수(Prime Number)를 찾는 효율적인 알고리즘입니다.
이 방법은 주어진 숫자 범위 내에서 소수를 구하는 데 사용됩니다.

🔎 알고리즘 개요

에라토스테네스의 체는 다음과 같은 단계로 작동합니다:

초기화:

2부터 원하는 숫자 범위의 최대값까지 모든 숫자를 나열합니다.
소수 판별을 위한 배열을 준비하고, 2부터 시작해 해당 배열에 모든 숫자를 "소수"로 가정하여 표시합니다.

소수 판별:

가장 작은 소수인 2부터 시작합니다. 2의 배수는 모두 소수가 아니므로 제외합니다. (2는 소수이므로 남겨둡니다.)
다음으로, 남아 있는 가장 작은 숫자를 찾고 그 숫자의 배수들을 모두 제거합니다.
이 과정을 나열된 숫자 중 남은 가장 작은 수에 대해 반복합니다. 해당 숫자가 이미 제거되었다면, 그 다음 숫자로 넘어갑니다.
최대값의 제곱근까지 이 과정을 반복합니다.

결과:

남아 있는 숫자는 모두 소수입니다.

예제

예를 들어, 1부터 30까지의 숫자에서 소수를 찾는 과정은 다음과 같습니다:

2부터 시작하여 2의 배수(4, 6, 8, 10, ..., 30)를 모두 지웁니다.
남은 숫자 중 3은 소수이므로, 3의 배수(9, 12, 15, ..., 30)를 모두 지웁니다.
4는 이미 지워졌으므로, 5를 확인합니다. 5는 소수이므로, 5의 배수(10, 15, 20, ..., 30)를 모두 지웁니다.
이 과정을 반복하여 남아 있는 숫자들(2, 3, 5, 7, 11, 13, 17, 19, 23, 29)이 소수가 됩니다.

장점

효율적: 에라토스테네스의 체는 단순하지만 매우 효율적입니다. 주어진 범위 내의 모든 소수를 찾는 데 걸리는 시간 복잡도는
nlogn입니다.
직관적: 알고리즘의 작동 방식이 직관적이고 이해하기 쉽습니다.

단점

메모리 사용: 숫자 범위가 커질수록 메모리 사용량도 증가합니다. 매우 큰 숫자 범위에서는 메모리 최적화가 필요할 수 있습니다.
에라토스테네스의 체는 소수를 빠르고 효율적으로 찾는 방법으로, 특히 컴퓨터 과학과 수학에서 널리 사용됩니다.

💻 에라토스테네스의 체 Java 구현

import java.util.Arrays;

public class SieveOfEratosthenes {
    public static void main(String[] args) {
        int n = 30;  // 1부터 30까지의 소수를 찾기
        boolean[] isPrime = new boolean[n + 1];

        // 모든 숫자를 소수로 가정하고 true로 초기화
        Arrays.fill(isPrime, true);

        // 0과 1은 소수가 아니므로 false로 설정
        isPrime[0] = false;
        isPrime[1] = false;

        // 2부터 시작하여 제곱근 이하까지 반복
        for (int i = 2; i * i <= n; i++) {
            if (isPrime[i]) {
                // i의 배수들을 모두 소수가 아니라고 표시
                for (int j = i * i; j <= n; j += i) {
                    isPrime[j] = false;
                }
            }
        }

        // 소수 출력
        System.out.println("소수 목록:");
        for (int i = 2; i <= n; i++) {
            if (isPrime[i]) {
                System.out.print(i + " ");
            }
        }
    }
}

💡 설명

초기화:

boolean[] isPrime = new boolean[n + 1];는 숫자 0부터 n까지의 소수 여부를 저장하는 배열입니다. 인덱스가 숫자에 해당하고, 값이 true면 그 숫자가 소수라고 가정합니다.
Arrays.fill(isPrime, true);를 사용하여 모든 숫자를 처음에는 소수로 간주합니다.
isPrime[0]과 isPrime[1]은 소수가 아니므로 false로 설정합니다.

소수 판별:

for (int i = 2; i * i <= n; i++)에서, 2부터 시작하여 n의 제곱근까지 반복합니다.
if (isPrime[i])를 통해 현재 숫자가 소수인지 확인하고, 소수라면 그 숫자의 배수들을 모두 false로 설정합니다.

결과 출력:

마지막으로, 소수로 남은 숫자들을 출력합니다.
실행 결과
위 코드가 실행되면, 1부터 30까지의 소수가 출력됩니다:

소수 목록:
2 3 5 7 11 13 17 19 23 29

이 코드는 원하는 범위 내에서 소수를 빠르고 효율적으로 찾을 수 있는 방법을 보여줍니다. n 값을 변경하여 다른 범위의 소수를 찾을 수도 있습니다.