그래프에서 경로를 찾는 두 가지 방법 (DFS, BFS)

자료 구조에서는 데이터를 어떻게 구축할지 고민하고,
알고리즘에서는 자료구조에서 어떤 순서와 방식으로 탐색할지 고민해야 한다.

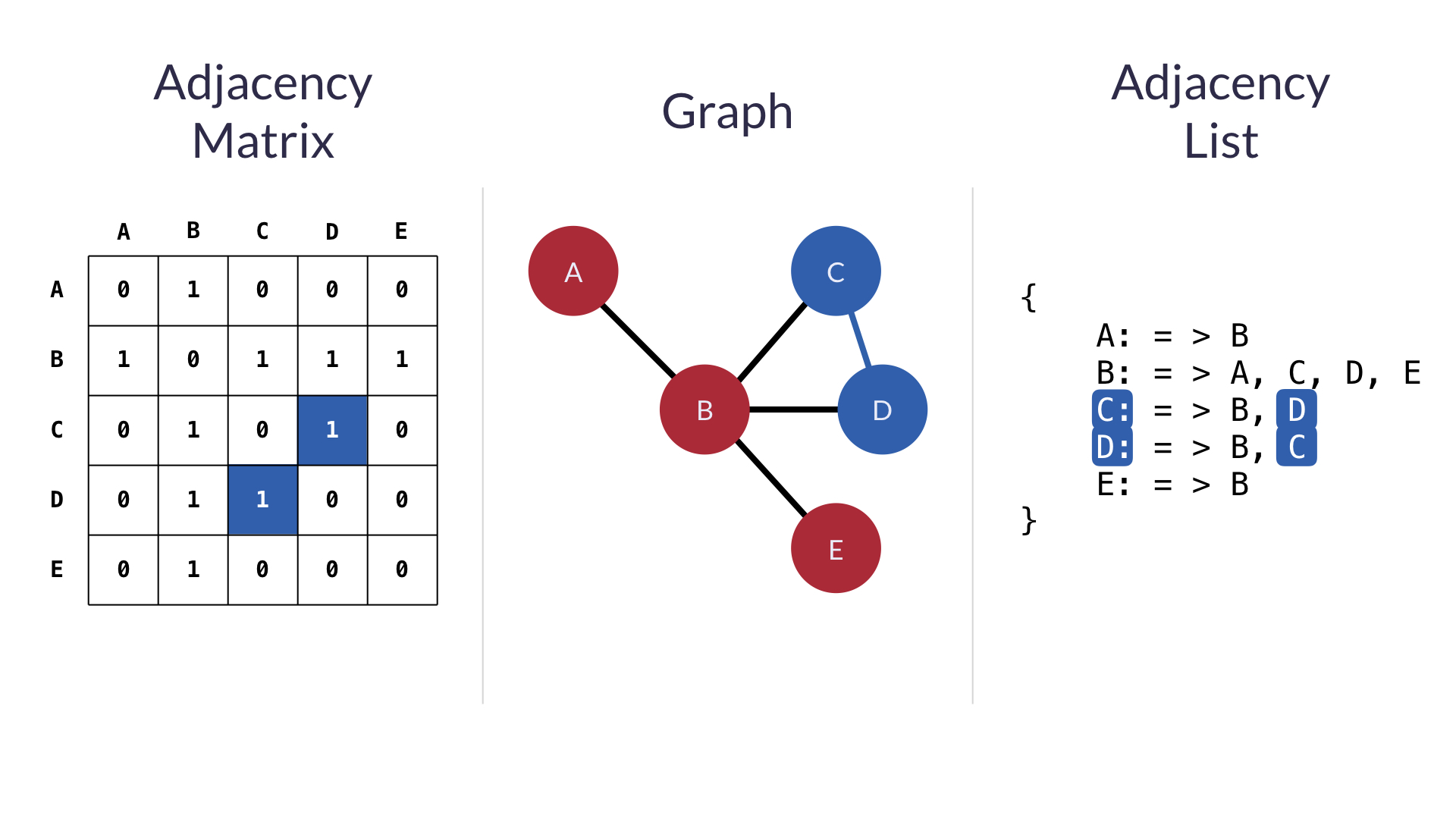
그래프 구현 방식

• 인접 행렬 adjacency matrix : 노드에 비해 간선수가 적은 희소 그래프에 쓰임. 시간 복잡도가 O(1)로 좋지만 노드가 모두 연결된 경우 NXN 크기의 인접행렬 필요
• 인접 리스트 adjacency list : 정점에 연결된 간선의 정보를 빠르게 알 수 있음. 시간 복잡도 O(N), 공간 복잡도는 O(E+V)로 인접행렬보다 이득. 다만 연결된 간선을 전부 확인해야해서 느림 -> 그래도 더 많이 씀.

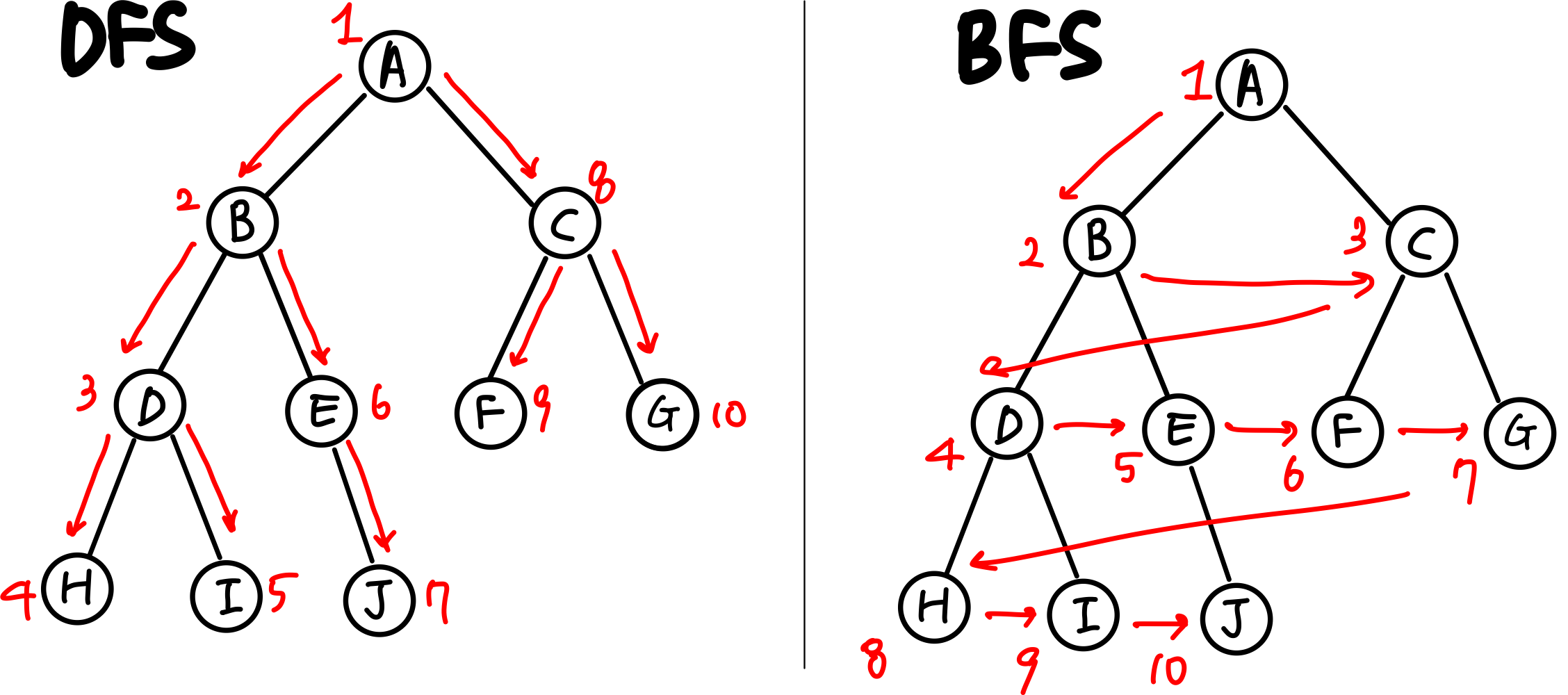
그래프에서 경로를 찾는 두 가지 방법

• 깊이 우선 탐색 : 깊게 탐색 후 되돌아오는 특성이 있음.
  ex) 모든 가능한 해를 찾는 백트래킹 알고리즘, 그래프의 사이클
  -> 최단 경로 아니면 깊이 우선 탐색 고려하기!
• 너비 우선 탐색 : 가중치가 없는 그래프에서 최단 경로를 보장.
  ex) 미로찾기에서 최단경로 찾기, 네트워크 분석

📌 깊이 우선 탐색

방식1

1. 스택이 비었는지 확인. 스택이 비었다는 건 모드 노드를 방문했다는 듯으로 탐색 종료
2. 스택에서 노드를 pop합니다.
3. pop한 노드의 방문 여부 확인. 방문하지 않았다면 방문 처리
4. 방문한 노드와 인전한 모든 노드 확인. 이중 방문하지 않은 노드를 스택에 push. 이때 오름차순을 고려한다면 역순으로 push해야함

고려사항

1. 가장 깊은 노드까지 방문한 후
2. 더 이상 방문할 노드가 없으면 최근 방문한 노드로 돌아온 다음
3. 해당 노드에서 방문할 노드가 있는지 확인한다.

방식2 : 재귀함수 - 시스템 스택에 함수 쌓기

📌 너비 우선 탐색

방식

1. 큐가 비었는지 확인. 큐가 비었다면 모든 노드를 확인했다는 의미로 탐색을 종료
2. 큐에서 노드를 poll 한다
3. poll한 노드와 인접한 모든 노드를 확인하고 그중 아직 방문하지 않은 노드를 큐에 add하며 방문처리

고려사항

1. 현재 방문한 노드와 직접 연결된 모든 노드를 방문할 수 있어야 한다
2. 이미 방문한 노드인지 확인할 수 있어야 한다

방문처리시점 차이

• 깊이 우선 탐색 : stack은 다음에 방문할 인접한 노드를 push. pop하며 방문처리
• 너비 우선 탐색 : 큐에 add하며 방문 처리