쿼드 트리 알고리즘 - 쿼드압축 후 개수 세기 (Java)

마법사 슬기·2024년 4월 23일

알고리즘 쿼드트리알고리즘 프로그래머스

알고리즘

목록 보기

5/9

오늘 풀어볼 문제는 프로그래머스의 "쿼드압축 후 개수 세기"입니다.

해당 문제는
"쿼드 트리 알고리즘" 을 이해하고, 이를 코드로 구현해보는 문제입니다.

✏️ 쿼드 트리 알고리즘

📍 정의

쿼드 트리 압축은 이미지를 4개의 영역으로 나누어 각 영역이 동일한 값으로 이루어져 있는지 확인합니다.
만약 그렇다면 해당 영역을 한 개의 값으로 압축하여 저장하고, 그렇지 않다면 영역을 재귀적으로 나누어 압축을 시도합니다.
이러한 방식을 통해 이미지의 일부 또는 전체를 효율적으로 압축할 수 있습니다.

따라서 쿼드트리 알고리즘은 재귀를 통해 분할 정복 방법론을 구현한 것으로 이해할 수 있습니다.

📍 기본 아이디어

이미지를 작은 사각형 영역으로 분할합니다.
각 영역이 특정 조건을 만족하는지 확인합니다. 예를 들어, 모든 픽셀의 색상이 동일한 경우 등의 조건을 확인할 수 있습니다.
2-1 만약 조건을 만족하지 않는다면 영역을 더 작은 영역으로 분할하고 재귀적으로 위의 과정을 반복합니다.
2-2 만약 조건을 만족한다면 해당 영역을 하나의 단일 노드로 표현합니다.

📍 사용

이는 이미지나 비트맵 데이터와 같은 2차원 배열을 효율적으로 압축하기 위해 사용되는 기술입니다.
주로 이미지 처리나 컴퓨터 그래픽스 분야에서 사용됩니다.

💡 재귀 문제를 해결하는 핵심 포인트

Base Case 정의
: 재귀 함수에서는 반드시 종료 조건을 명확하게 정의해야 합니다. 이를 Base Case라고 합니다. Base Case를 정의하지 않으면 무한히 재귀 호출이 일어나 스택 오버플로우가 발생할 수 있습니다.
작은 문제로 분할
: 재귀 함수는 큰 문제를 작은 문제들로 분할하여 해결합니다. 각 재귀 호출에서는 문제의 크기가 작아지도록 만들어야 합니다.
재귀 호출
: 작은 문제들을 해결하기 위해 자기 자신을 호출합니다. 이때 입력값이나 상태가 변경되어야 하며, 이를 통해 Base Case에 도달하도록 합니다.
결과 합치기
: 작은 문제들을 해결한 결과를 합쳐서 큰 문제의 해답을 얻습니다. 종종 이러한 결과들을 재귀 호출의 결과로 반환하거나 전역 변수를 통해 누적합니다.
재귀 호출의 깊이 제한
: 재귀 호출의 깊이가 너무 깊어지면 스택 오버플로우가 발생할 수 있으므로, 문제 특성에 맞게 적절한 재귀 호출의 깊이를 설정해야 합니다.

깨알코너, "작은 문제"를 다루는 재귀와 동적 프로그래밍 헷갈리지 말자! (더보기)

🤷‍♀️ 재귀와 동적프로그래밍

재귀

재귀는 주로 "분할 정복" 방식을 사용합니다.
큰 문제를 작은 문제로 나누고 이를 해결하는 과정에서 계속해서 재귀적으로 자신을 호출합니다.
이러한 과정에서 기본적으로 "큰 것에서 작은 것"으로 해결 방식을 취합니다.

동적프로그래밍

동적 프로그래밍은 문제를 해결하기 위해 "작은 아이디어"에서 시작합니다.
주어진 문제를 작은 부분 문제로 나누고, 각각의 부분 문제를 해결하면서 이전에 계산된 결과를 저장하고 재활용하여 중복 계산을 피합니다.
이는 보통 반복문을 사용하여 구현되며, 작은 부분 문제들을 해결하고 그 결과를 테이블에 저장하는 방식입니다.
이러한 과정에서 "작은 것에서 큰 것"으로 해결 방식을 취합니다.

물론 이 두 가지 접근 방식은 문제의 특성과 성격에 따라 적합한 방법이 다를 수 있습니다.
때로는 동적 프로그래밍으로 풀 수 있는 문제가 재귀로 풀기도 하고, 그 반대의 경우도 있습니다.
하지만 일반적으로는 위에서 설명한 대로 재귀와 동적 프로그래밍은 각각 다른 문제 해결 방법을 제공합니다.

🔎 프로그래머스 :: 쿼드압축 후 개수 세기

문제 설명
0과 1로 이루어진 2n x 2n 크기의 2차원 정수 배열 arr이 있습니다.
당신은 이 arr을 쿼드 트리와 같은 방식으로 압축하고자 합니다. 구체적인 방식은 다음과 같습니다.
당신이 압축하고자 하는 특정 영역을 S라고 정의합니다.
만약 S 내부에 있는 모든 수가 같은 값이라면, S를 해당 수 하나로 압축시킵니다.
그렇지 않다면, S를 정확히 4개의 균일한 정사각형 영역(입출력 예를 참고해주시기 바랍니다.)으로 쪼갠 뒤, 각 정사각형 영역에 대해 같은 방식의 압축을 시도합니다.
arr이 매개변수로 주어집니다. 위와 같은 방식으로 arr을 압축했을 때, 배열에 최종적으로 남는 0의 개수와 1의 개수를 배열에 담아서 return 하도록 solution 함수를 완성해주세요.

제한사항
arr의 행의 개수는 1 이상 1024 이하이며, 2의 거듭 제곱수 형태를 하고 있습니다. 즉, arr의 행의 개수는 1, 2, 4, 8, ..., 1024 중 하나입니다.
arr의 각 행의 길이는 arr의 행의 개수와 같습니다. 즉, arr은 정사각형 배열입니다.
arr의 각 행에 있는 모든 값은 0 또는 1 입니다.

입출력 예
arr result
{{1,1,0,0},{1,0,0,0},{1,0,0,1},{1,1,1,1}} {4,9}
{{1,1,1,1,1,1,1,1},{0,1,1,1,1,1,1,1},{0,0,0,0,1,1,1,1},{0,1,0,0,1,1,1,1},{0,0,0,0,0,0,1,1},{0,0,0,0,0,0,0,1},{0,0,0,0,1,0,0,1},{0,0,0,0,1,1,1,1}} {10,15}

입출력 예 설명
입출력 예 #1

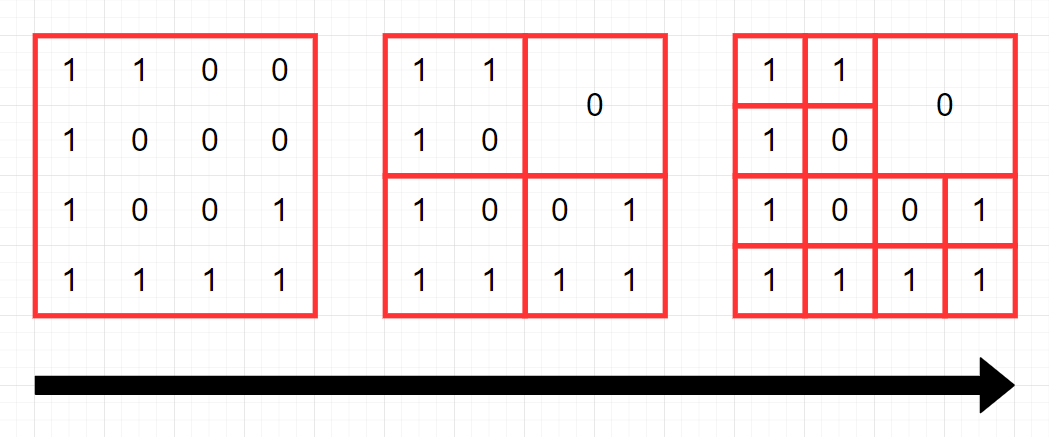
다음 그림은 주어진 arr을 압축하는 과정을 나타낸 것입니다.
최종 압축 결과에 0이 4개, 1이 9개 있으므로, [4,9]를 return 해야 합니다.

입출력 예 #2

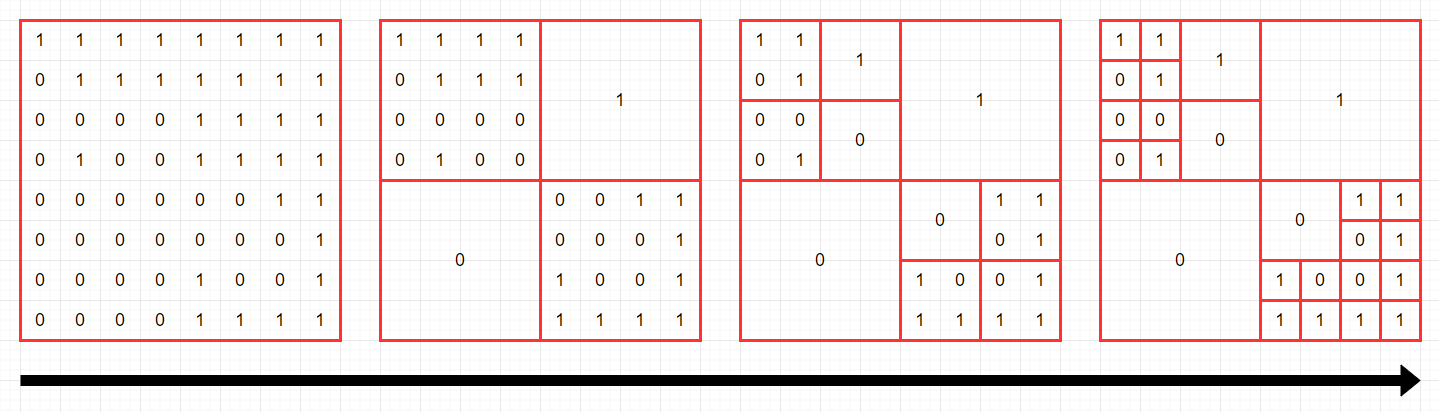
다음 그림은 주어진 arr을 압축하는 과정을 나타낸 것입니다.
최종 압축 결과에 0이 10개, 1이 15개 있으므로, [10,15]를 return 해야 합니다.

재귀의 핵심 포인트를 바탕으로 수도 코드를 작성해보겠습니다.

💡 sudo code

함수 쿼드트리:
    만약 영역 전체가 같은 숫자라면: (재귀 호출 여부 판단)
        만약 그 숫자가 0이면:
            0의 개수를 증가시킴
        그렇지 않으면:
            1의 개수를 증가시킴
    그렇지 않으면:
        배열을 네 개로 나눠 쿼드트리 호출 (재귀호출)

코드로 이해하면 아래와 같습니다.

💻 Java Code

class Solution {
    int[] answer = new int[2];
    
    public int[] solution(int[][] arr) {
        quard(arr, 0, 0, arr.length); // 쿼드 트리 알고리즘을 호출하여 압축 수행
        return answer; // 결과 반환
    }

    // 주어진 영역이 압축 가능한지 여부를 판단하는 함수
    public boolean zip(int[][] arr, int x, int y, int len) {
        int pointer = arr[x][y];

        // 영역 내의 모든 값이 같은지 확인하여 압축 가능 여부 판단
        for(int i=x; i<x+len; i++) {
            for(int j=y; j<y+len; j++) {
                if(pointer != arr[i][j]) return false; // 값이 다르면 압축 불가능
            }
        }
        return true; // 모든 값이 같으면 압축 가능
    }

    // 이미지를 재귀적으로 분할하여 쿼드 트리 압축을 수행하는 함수
    public void quard(int[][] arr, int x, int y, int len) {

        // 압축할 수 있다면
        if(zip(arr, x, y, len)) {
            if(arr[x][y] == 0) answer[0]++;     // 압축 가능하고 0인 경우 0의 개수 증가
            else answer[1]++;                   // 압축 가능하고 1인 경우 1의 개수 증가
            return;                             // 현재 영역은 더 이상 분할할 필요 없음

        // 압축할 수 없다면 잘라서 다시 압축 시도
        } else {
            quard(arr, x, y, len/2);            // 왼쪽 위 사분면
            quard(arr, x, y+len/2, len/2);      // 오른쪽 위 사분면
            quard(arr, x+len/2, y, len/2);      // 왼쪽 아래 사분면
            quard(arr, x+len/2, y+len/2, len/2);// 오른쪽 아래 사분면
        }
    }
}