우선순위 큐(Priority Queue)
- 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조.
- 데이터를 우선순위에 따라 처리하고 싶을 때 사용.
- 물건 데이터를 자료구조에 넣었다가 가치가 높은 물건부터 차례대로 확인해야하는 경우.
| 자료구조 | 추출되는 데이터 |
|---|---|
| 스택(Stack) | 가장 나중에 삽입된 데이터 |
| 큐(Queue) | 가장 먼저 삽입된 데이터 |
| 우선순위 큐(Priority Queue) | 가장 우선순위가 높은 데이터 |
구현방법
- 리스트 이용
- 리스트에 차례대로 데이터를 넣은 다음, 리스트에서 꺼낼때는 각각의 데이터를 확인 한 후 추출.
- 삽입: 차례대로 데이터 넣음 O(1), 삭제: 각 데이터 확인 후 추출 O(N)
- 힙(heap) 이용
-
데이터의 개수가 N개일 때, 구현 방식에 따라서 시간 복잡도 비교.
우선순위 큐 구현방식 삽입시간 삭제시간 리스트 O(1) O(N) 힙(Heap) O(logN) O(logN) -
단순히 N개의 데이터를 힙에 넣었다가 모든 꺼내는 작업은 정렬과 동일(Heap 정렬)
- 시간복잡도: O(logN)
Heap
- 완전 이진 트리 자료구조.
- 항상 루트 노드(root node) 제거.
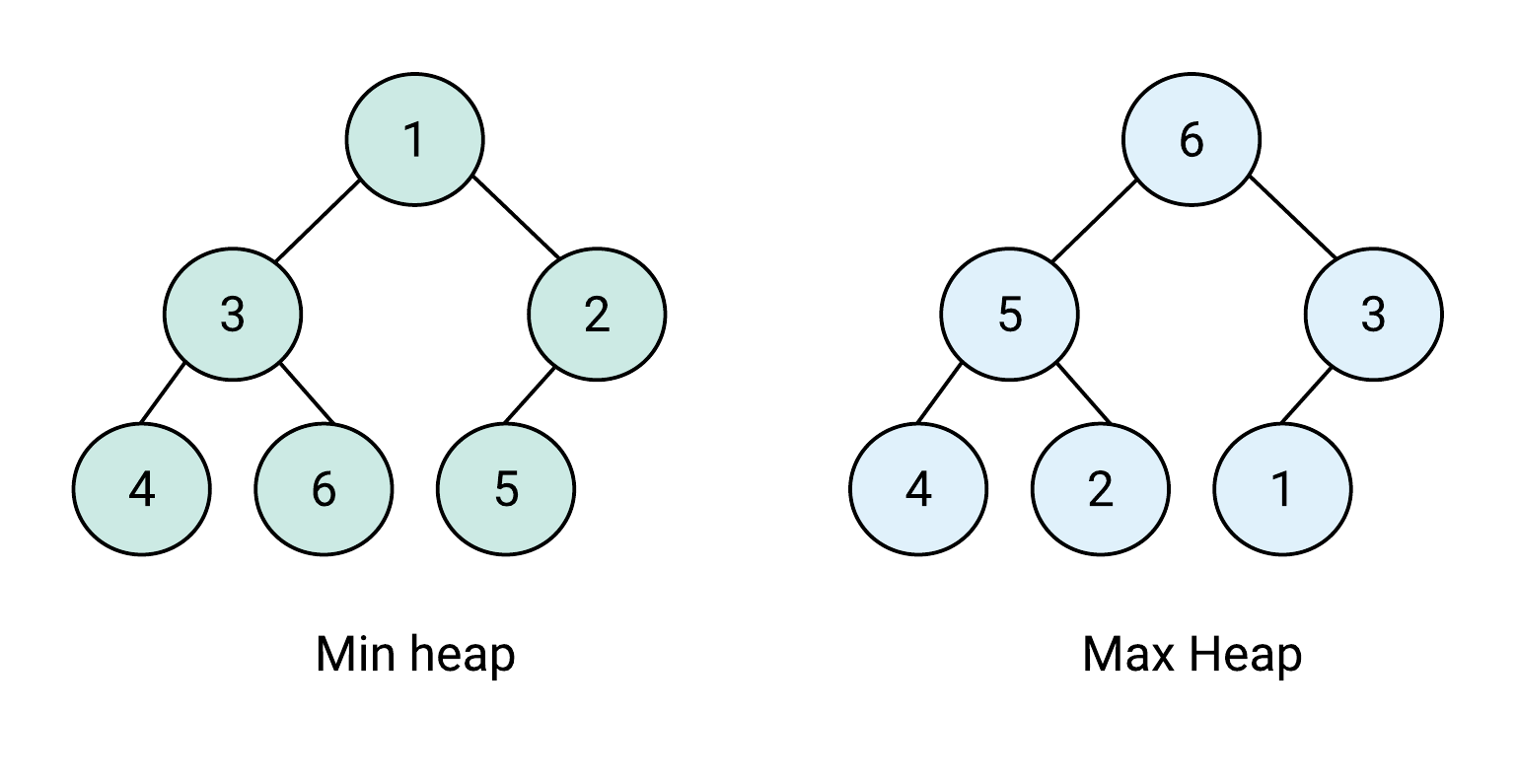
최소 힙(mini heap)
- 루트 노드가 가장 작은 값을 가짐.
- 값이 작은 데이터가 우선적으로 제거.
최대 힙(max heap)
- 루트 노드가 가장 큰 값을 가짐.
- 값이 큰 데이터가 우선적으로 제거.
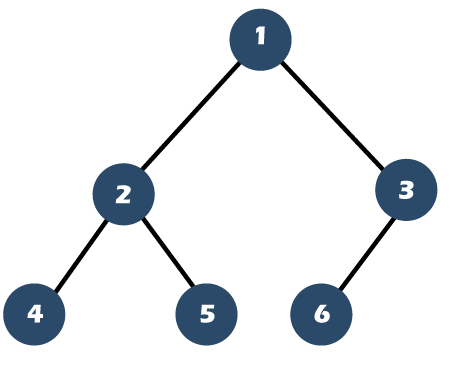
완전 이진 트리(Complete Binary Tree)
- 루트 노드부터 시작하여 왼쪽 자식 노드, 오른쪽 자식 노드 순서대로 데이터가 삽입되는 트리.
최소 힙 구성 함수: Min-Heapify()
- (상향식) 부모 노드로 거슬러 올라가며, 부모보다 자신의 값이 더 작은 경우에 위치를 교체.
힙에 새로운 원소 사입
- 새로운 원소가 삽입되었을 때 O(logN)의 시간복잡도 유지.
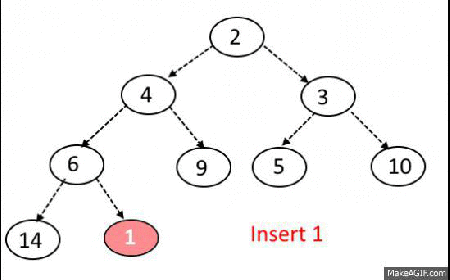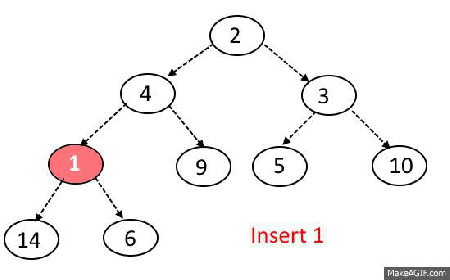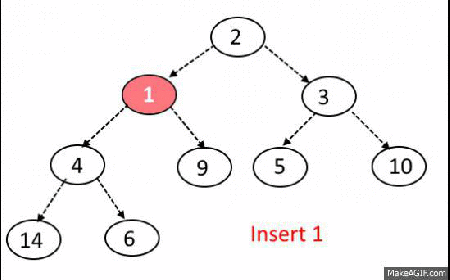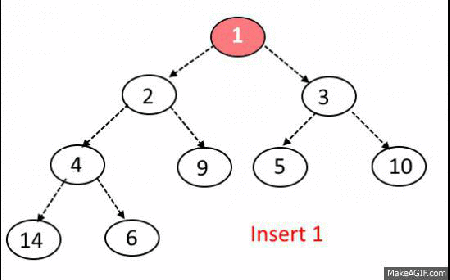
힙에서 원소 제거
- 힙에서 원소가 제거되었을 때 O(logN)의 시간복잡도 유지.
- 가장 마지막 노드가 루트 노드의 위치로 오게함.
- 이후 루트노에서 하향식(더 작은 자식노드로)으로 Heapify() 진행.
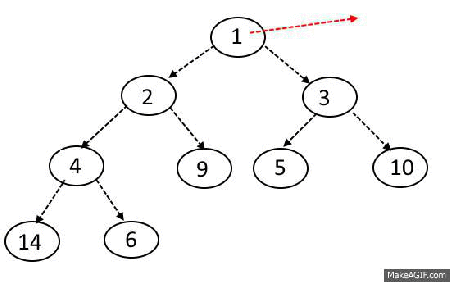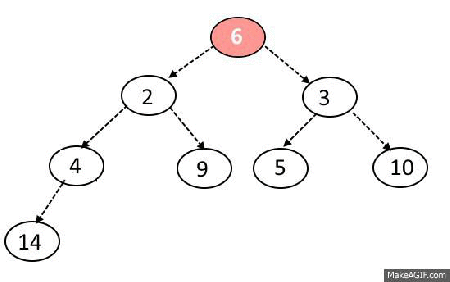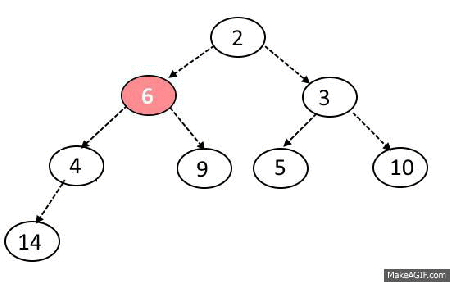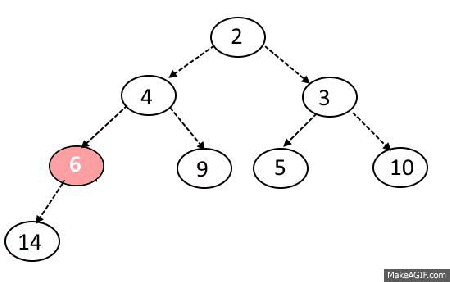
우선 순위 큐 라이브러리르 활용한 힙 정렬 구현 예제(Python)
import sys
import heapq
input = sys.stdin.readline
def heapsort(iterable):
h=[]
result=[]
# 모든 원소를 차례대로 힙에 삽입
for value in iterable:
heapq.heappush(h, value)
# 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
for i in range(len(h)):
result.append(heapq.heappop(h))
return result
n = int(input())
arr=[]
for i in range(n):
arr.append(int(input()))
res = heapsort(arr)
for i in range(n):
print(res[i]) # python은 기본적으로 min heap 형태로 동작 -> 오름차순 정렬
- python은 기본적으로 min-heap 형태로 동작 -> 오름차순 정렬 .
- max-heap 필요하다면 데이터를 넣을때와 꺼낼때 -를 붙여서 데이터를 꺼내게 되면 max-heap으로 동작.
for v in iterable:
heapq.heappush(h,-v)
for i in range(len(h)):
result.append(heapq.heappop(h)*-1)
return result