자료구조 - 트리(Tree)

Tree(트리)

• 가계도와 같은 계층적인 구조 표현.
• 기본적으로 트리의 크기가 N일때, 전체 간선의 개수는 N-1개.
  

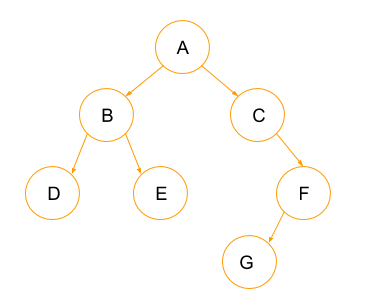
트리 관련용어

• 루트 노드(root node): 부모가 없는 최상위 노드.
• 단말 노드(leaf node): 자식이 없는 노드.
• 크기(size): 트리에 포함된 모든 노드의 개수.
• 깊이(depth): 루트 노드부터의 거리.
• 높이(height): 깊이 중 최댓값.
• 차수(degree): 각 노드의(자식방향) 간선 개수.

이진탐색트리(Binary Search Tree)

• 이진 탐색이 동작할 수 있도록 고안된 자료구조.

이진 탐색 트리의 특징

왼쪽 자식 노드 < 부모 노드< 오른쪽 자식 노드

• 부모 노드보다 왼쪽 자식 노드가 작음.
• 부모 노드보다 오른쪽 자식 노드가 큼.

트리의 순회(Tree Traversal)

• 트리 자료구조에 포함된 노드를 특정한 방법으로 한 번씩 방문하는 방법.
  • 트리의 정보를 시각적으로 확인.

대표적인 트리순회방법

• 전위 순회(pre-order traverse): 루트를 먼저 방문.
• 중위 순회(in-order traverse): 왼쪽 자식을 방문한 뒤에 루트를 방문.
• 후위 순회(post-order treavers): 오른쪽 자식을 방문한 뒤에 루트를 방문.

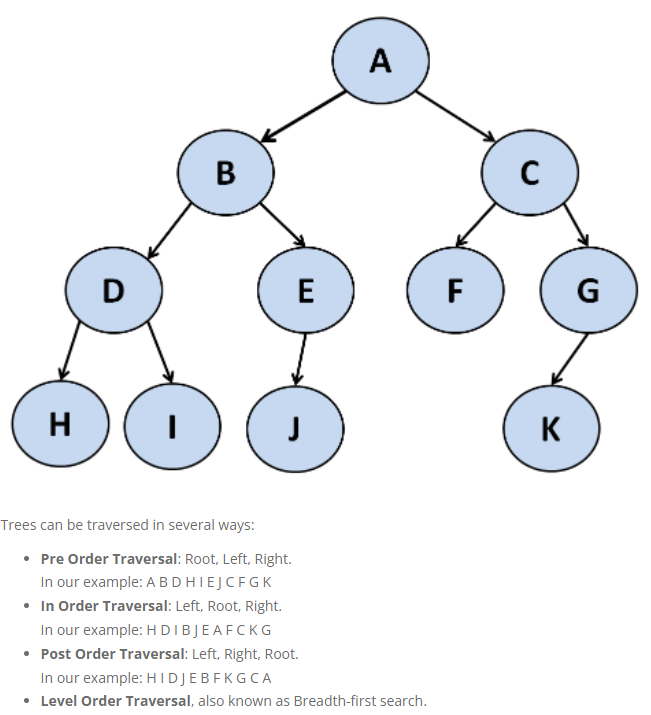
트리의 순회 구현 예제

Class Node:
	def __init__(self,data,left_node,right_node):
    	self.data = data
        self.left_node = left_node
        self.right_node = right_node
        
# 전위 순회(PreOrder Traversal)
def pre_order(node):
	print(node.data, end=' ')
    if node.left_node != None:
    	pre_order(tree[node.left_node])
    if node.right_node != None:
    	pre_order(tree[node.right_node])
        
# 중위 순회(InOrder Traversal)
def in_order(node):
    if node.left_node != None:
    	in_order(tree[node.left_node])
    print(node.data, end=' ')
    if node.right_node != None:
    	in_order(tree[node.right_node])
        
# 후위 순회(PostOrder Traversal)
def post_order(node):
    if node.left_node != None:
    	post_order(tree[node.left_node])
    if node.right_node != None:
    	post_order(tree[node.right_node])
    print(node.data, end=' ')
    
n = int(input())
tree = {}

for i in range(n):
	data, left_node, right_node = input().split()
    if left_node == "None":
    	left_node = None
    if right_node == "None":
    	right_node = None
    tree[data] = Node(data, left_node, right_node)
pre_order(tree['A'])
print()
in_order(tree['A'])
print()
post_order(tree['A'])

# 입력
7
A B C
B D E
C F G
D None None
E None None
F None None
G None None

# 결과
A B D E C F G 
D B E A F C G 
D E B F G C A